Non-singular matrix in Discrete mathematicsIf the determinant of the given matrix is equal to a non-zero value, then the matrix will be a non-singular matrix. The non-singular matrix must be a square matrix. The non-singular matrix contains a property, i.e., we can find the inverse of a non-singular matrix because this matrix contains a non-zero value in the result of determinant. In this section, we will learn about non-singular matrices, calculating 2D and 3D determinants, how to find a non-singular matrix, their properties, examples, and many more things. What is Non-singular matrixA matrix will be known as a non-singular matrix if it is a square matrix and the determinant of this matrix is not equal to 0. This matrix is a kind of inverse matrix, and we can find the inverse of this matrix because it contains the determinant value. Suppose there is a square matrix A, where 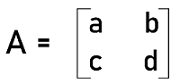
This matrix will be known as the non-singular matrix A if and only if its determinant is equal to a non-zero value, i.e., |A| = |ad - bc| ≠ 0 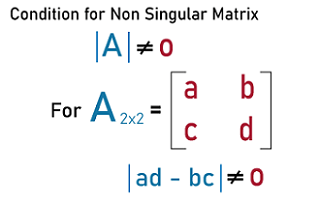
Finding a Non-singular matrixWe can find that the given matrix is singular or non-singular with the help of finding the determinant of the matrix. In case of the non-singular matrix, we will get a non-zero value as the result of determinant. There are two ways through which we can find the determinant of a non-singular matrix. In the first way, we can find the determinant of a matrix with the help of row or column operation. In the second way, we can use the cofactor of the elements of the matrix to determine the determinant. Rules for rows and column operations of a DeterminantThere are some rules which we should follow if we want to perform the rows and columns operations on determinants, which are described as follows:
The determinant will become the number itself if there is a square matrix with an order 1∗1, which is used to have only one number. Now we will see how we can calculate the determinants for the matrices which have second order and third order. Calculating 2D determinantsWith the help of determinant formula, we can calculate the determinant of a square matrix, which has an order 2∗2 or any 2D square matrix. Suppose we have the following square matrix of order 2∗2: 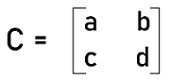
We can calculate the 2D determinant of this matrix in the following way: 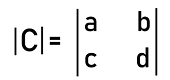
|C| = (a∗d ' b∗c) Calculating 3D DeterminantWith the help of following procedure, we can calculate the determinant of a square matrix, which has an order 3∗3 or any 3D square matrix. Suppose we have the following square matrix of order 3∗3: 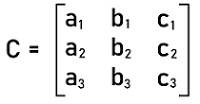
Here we will calculate the determinant of above matrix with the help of first row. So first, we will multiply the elements of first row a1, b1, and c1 by their respective cofactors. We will get the value of determinant of the above square matrix when we do the summation of the product of elements with their respective cofactors. Alternatively, we can determine the determinant of a matrix with the help of elements of any particular row or column. 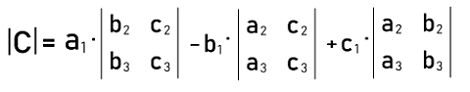
|C| = a1(b2c3 ' b3c2) ' b1(a2c3 ' a3c2) + c1(a2b3 ' a3b2) Properties of Non-singular matrixThe non-singular matrix is used to contain a lot of properties, and some of them are described as follows:
Terms related to Non-singular matrixThere are some terms that we should know while learning the concept of a non-singular matrix so that we can properly understand the non-singular matrix. These terms are described as follows: Singular matrix: A matrix will be known as the singular matrix if the determinant of this matrix is equal to 0. If there is a singular matrix A, then its determinant |A| = 0. It is not possible to do the inverse of a singular matrix. Minor: There is a minor for every element of a matrix. The minor of a particular element will be equal to the determinant which we get after eliminating the row and column which have this element. Now we will understand this with the help of an example. Suppose there is a matrix A which contains the following elements: 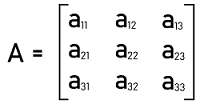
Now we will get the minor of element a11 like this: 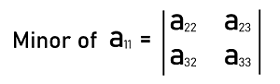
Determinant: The determinant of a matrix can be described as a single unique value representation of a matrix. In the non-singular matrix, we can use any row or column of the matrix and determine the determinant of that matrix. In other words, we can say that the determinant of matrix can be calculated with the help of addition of multiplication of elements and their cofactors of a particular row and column of the matrix. Adjoint matrix: We can calculate the adjoint of a matrix with the help of calculating the transpose of cofactor element matrix of the given matrix. Inverse of a matrix: This matrix is another type of matrix. If we multiply the inverse matrix and the given matrix, then it will generate a multiplicative identity as a result. Suppose there is a matrix with an order 2∗2. If we divide the adjoint of matrix by the determinant of that matrix, then we can get the inverse of that matrix, i.e., A-1 = 1/|A| adj A Examples of Non-singular matrixThere are a lot of examples of non-singular matrices, and some of them are described as follows: Example 1: In this example, we have a matrix A, and we have to determine whether this matrix is non-singular or not. The elements of matrix A are described as follows: 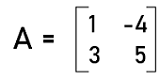
Solution: To find whether the given matrix is non-singular or not, we have to first determine the determinants of this matrix. From the question, we have the following matrix: 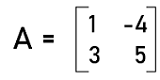
The above matrix is in the form of 2∗2 matrix, which is described as follows: 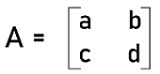
We have learned that the determinant of this matrix |A| will be calculated like this: |A| = |ad ' bc| So |A| = 1(5) ' 3(-4) = 5 ' (-12) = 5 + 12 |A| = 17 The determinant of this matrix is 17, which is not equal to 0. That's why this matrix is a non-singular matrix. Example 2: In this example, we have a matrix A, and we have to determine whether this matrix is non-singular or not. The elements of matrix A are described as follows: 
Solution: To find whether the given matrix is non-singular or not, we have to first determine the determinants of this matrix. From the question, we have the following matrix: 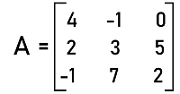
Here we will use the cofactors of 1st row elements and try to calculate the determinant of the matrix A in the following way: |A| = 4[3(2) ' 5(7)] + 1[2(2) ' (-1)(5)] + 0[2(7) ' (-1)(3)] |A| = 4[6 ' 35] + 1[4 + 5] + 0[14 + 3] |A| = 4[-29] + 1[9] + 0[17] |A| = -116 + 19 + 0 |A| = -97 The determinant of this matrix is -97, which is not equal to 0. That's why this matrix is a non-singular matrix.
Next TopicOrder of matrix in Discrete mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









