Doolittle Algorithm: LU DecompositionIn this section, we will learn about the LU decomposition of a matrix with the help of Doolittle's algorithm. Here LU can also be known as the "LU factorization", where LU stands for 'Lower Upper'. In 1938, the famous mathematician Tadeusz Banachiewicz was introduced the LU decomposition. In the Doolittle algorithm, we will factor the matrix in the form of multiplication of a lower triangular matrix and upper triangular matrix in the case of numerical analysis and linear analysis. With the help of LU decomposition, computers can be solved the square systems of linear equations. At the time of computing the determinant of matrix or inverting a matrix, this will be a key step. Suppose there is a square matrix which is indicated by A. An LU factorization can be described as the factorization of A with proper column and/or rows permutation or order, which will be divided into two factors, i.e., a lower triangular matrix, which is represented by L, and an upper triangular matrix, which is represented by U. So A = LU. 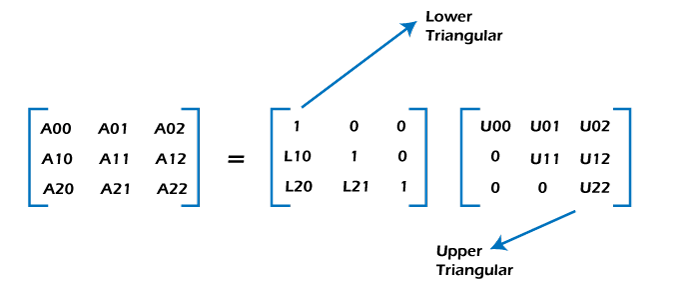
Doolittle AlgorithmA square matrix can be easily factored into a lower triangular matrix and upper triangular matrix, which is described as follows:
[A] = [L] [U]
We have one more way to factor A into an LU decomposition, which is Doolittle's method. This method allows us to do factor without going through the hassle of Gaussian Elimination. Suppose there is an n * n matrix A. Here we will assume that this matrix also contains the LU decomposition, and we will explicitly write the form of L and U. After that, we will use the systematic manner to solve the entries in L and U with the help of equations that result from the multiplications necessary for A = LU. The terms used for the U matrix are described as follows: 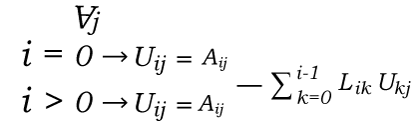
And the term which is used for the L matrix is described as follows: 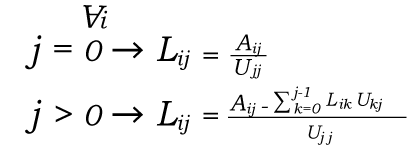
Examples of LU decomposition:Example 1: Input: 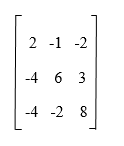
Output: 
Example 2: In this example, we will find the LU decomposition with the help of using Doolittle's method of the given matrix: 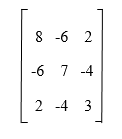
Solution: According to the Doolittle algorithm, A = LU So 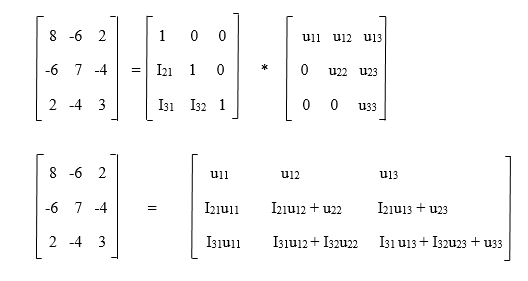
The above matrix implies that: u11 = 8 u12 = -6 u13 = 2 I21u11 = -6 ⇒ I21 * 8 = -6 ⇒ I21 = -3/4 I21u12 + u22 = 7 ⇒ (-3/4) * (-6) + u22 = 7 ⇒ u22 = 5/2 I21u13 + u23 = -4 ⇒ (-3/4) × 2 + u23 = -4 ⇒ u23 = -5/2 l31u11 = 2 ⇒ l31 × 8 = 2 ⇒ l31 = 1 / 4 l31u12 + l32u22 = -4 ⇒ 1/4 × (-6) + l32 × 5/2 = -4 ⇒ l32 = -1 l31u13 + l32u23 + u33 = 3 ⇒ 1/4 × 2 + (-1) × (-5/2) + u33 = 3 ⇒ u33 = 0 A = L * U = LU 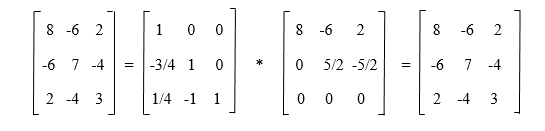
Doolittle's MethodHere we will describe the steps of a Doolittle method LU factorization of A when there is the unit value in the diagonal elements of lower triangular matrix L. Steps:
Example: X1 + X2 + X3= 5 X1 + 2X2 + 2X3 = 6 X1 + 2X2+ 3X3 = 8 Solution: 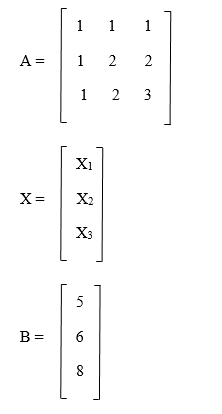
Suppose A = LU. So, 
Suppose Ly = B 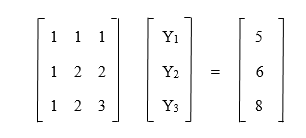
Y1 = 5 Y1 + Y2 = 6; Y2 = 1 Y1 + Y2 + Y3 = 8; Y3 = 2 Y1 = 5 Y2 = 1 Y3 = 2 Suppose Ux = Y 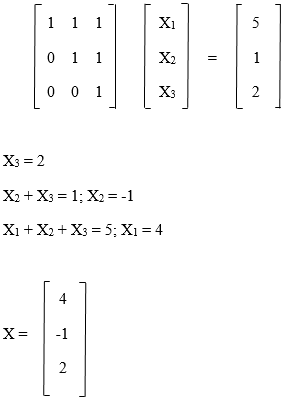
Next TopicRSA Encryption in Discrete Mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









