Constant Function in Discrete Mathematics

A constant function can be described as a quantity that stays constant over a period of time. Among all the real-valued functions, the constant function is considered as the simplest function. This function is a type of linear function. The graphs of this function in the plane are the horizontal lines. For the different inputs, this function always generates the same output. Now we will learn about the definitions, graphs, and solved examples of constant function.

Definition of Constant Function

A constant function can be described as a function that contains the same range for different values of the domain. In the graphical representation, the constant function will always be a straight line, which will be parallel to the x-axis. The x-axis is used to indicate the domain of the function, which contains the x value. The y-axis is used to indicate the range of the function, which contains y or f(x).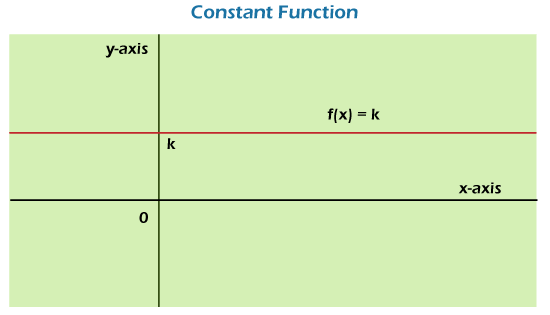

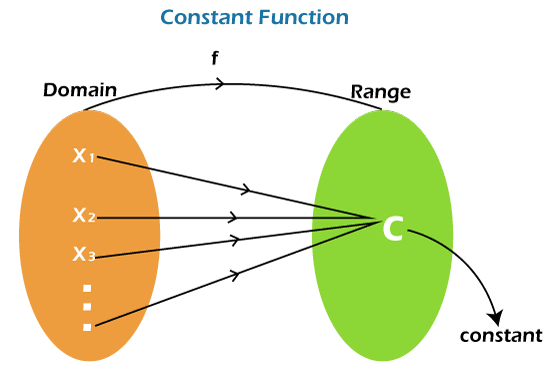
If the constant function is in the form y = k, then this function will be known as the constant function. Where y is used to indicate the real number and k is used to indicate a constant. We can also write y = k as f(x) = k. So we can say that the value of f(x) will always be k in all cases, and this f(x) will be independent of the value of x. In general, this function is a type of function that always contains the same constant value, which is not dependent on the input value. Now we will show some examples of a constant function, which is described as follows:

• f(x) = 0
• f(x) = 1
• f(x) = π
• f(x) = 3
• f(x) = -0.3412454
• f(x) can be equal to any other real number

The constant function contains a very interesting thing, i.e., we can take any kind of real number as input for our function x, and without using a calculator, we will instantly get the value of a function.

Finding of Constant Function

Here we will learn about the main difference between a constant function and a non-constant function. We will do the following things if we want to determine whether the function is a constant function:

• First, we will check that the given function generates different outputs for different inputs. If different outputs are generated, then the given function will not be a constant function.
• But if the function generates the same output for different inputs, then that type of function will be known as a constant function.

Now we will understand this concept with the help of following examples:

Example 1: In this example, we will assume a function y = x+ 2. Now we will find whether we can get the same output for the different input values for the given function.

Solution: We have a function y = x+2. Now we will take the different input values of x.

When input x = 1, then

y = 1+2 = 3

When input x = 2, then

y = 2+2 = 4

When input x = 3, then

y = 3+2 = 5

When input x = 4, then

y = 4+2 = 6

When input x = 5, then

y = 5+2 = 7

Since, we have different outputs for different inputs 1, 2, 3, 4, and 5. Hence, the given function y = x+2 is not a constant function.

Example 2: In this example, we will assume a function y = 4. Now we will find whether we can get the same output for the different input values of x for the given function.

Solution: We have a function y = 4.

Now we will notice that the output of y will always remain 4 no matter what our x value is.

When x = 3, then

y = 4

When x = 4, then

y = 4

When x = 5, then

y = 4

When x = 6, then

y = 4

So the value of y is always 4. It is not affected by the value of input x.

Hence, the function y = 4 is a constant function because it generates the same output for different inputs.

Graphs of Constant Function

Here we will see the look of constant function on a coordinate plane. Here we will see the graph of a constant function with the help of a horizontal line. As we have learned in the definition of a constant function is that a constant function is a type of real-valued function, and this function does not contain any type of variable. To understand this, we will assume a function f(x) = 3 where f: R → R.

• The above function shows that the output of this function will always be 3. It will not matter what input values we are inserting.
• In this graph, we can define some points that are (-1, 3), (2, 3), (4, 3), and so on.

In the following image, we can see the graph of a constant function f(x) = 3 like this: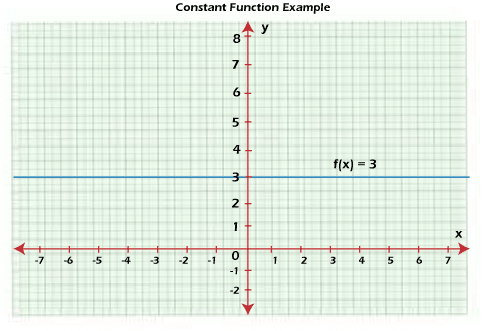

In the above graph, we can see that the y coordinates of all points are similar, i.e., 3. That's why the graph of a constant function f(x) = 3 is a horizontal line. So we can say that the graphs of all constant functions will also be the horizontal lines.

Characteristics of Constant Function

The vertical axis is used to cut the value of all the constant functions on the basis of the value of their constant. We cannot cut the constant function with the help of horizontal axis because constant functions are parallel to it. This function also indicates the horizontal line, which has the ability to extend on both sides without any break. That's why we can say that the constant functions are also continuous. There are a lot of properties of constant functions, which are described as follows:

Slope of a Constant Function

A constant function is a type of linear function, which can be indicated in the form y = mx+k. Here m and k are used to indicate the constants. If there is a constant function f(x) = k or y = k, then we can also write this function as y = 0x+k. When we compare the slope-intercept form y = mx+b with the equation y = 0x+k, then we will see that its slope will be m = 0. So we can say that for a constant function, the slope will always be 0.

Domain and Range of a Constant Function

A constant function can be described as a linear function. The range of this function only has one element, which is irrespective of the number of domain elements. For all the real values of x, the constant function can be defined in the following ways:

• The domain of this function is a set of all real numbers R. So, domain = R.
• If we have a constant function f(x) = k, then the output of this function will only be one, i.e., k. The range of this function will be a set that contains only one element k. So Range = {k}.

Derivatives of a Constant Function

Among all the functions, the simplest function is the constant function, and we can very easily compute the derivative of this function. We can determine the derivative of a constant function with the help of direct substitution. For a constant function, the differentiation rule is described as follows:

With the help of above differentiation, we can say that the derivation of a constant function is 0. We can also consider the derivatives of a function to be a slope of the tangent line at any given point, and we have already learned that zero is the slope of a constant function. Now we will understand this function and their respective derivative with the help of an example. Suppose the constant function y = -1 and the derivative of this function is y' = 0.

Limit of a Constant Function

The property of limits states that the limit of a constant function will always be equal to the constant itself. If there is an instance that contains a function y = 6, in this case, the limit of this function will also be 6. We can represent limit in the following way:

Constant Functions in real world

We can find the application of this function in real life in a lot of places. Here the constant functions are able to model the situations where one parameter is used to indicate a constant, and this parameter cannot vary because of the other independent parameters. There are a lot of examples of constant functions in the real world, and some examples of constant functions are described as follows:

• In a departmental store, the cost of any item is 300rs.
• In a book store, the cost of any type of book is 400rs.
• In an office, every employee gets an equal hike in their salary no matter how hard they all work.
• In a store, every person gets a price worth 200rs who purchases the item beyond 2000rs.
• In a school canteen, each and every student gets one paratha irrespective of their age and grades.

Important notes on constant function

When we learn about the constant function, there are some points that we should keep in our mind, which are described as follows:

• The graph of a constant function cannot be in the form of a curve.
• The graph of a constant function will always be in the form of a horizontal line.
• If there is an algebraic function that does not contain any variable, in this case, the algebraic function will be known as the constant function.