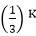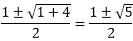Linear Recurrence Relations with Constant CoefficientsA Recurrence Relations is called linear if its degree is one. The general form of linear recurrence relation with constant coefficient is C0 yn+r+C1 yn+r-1+C2 yn+r-2+⋯+Cr yn=R (n) Where C0,C1,C2......Cn are constant and R (n) is same function of independent variable n. A solution of a recurrence relation in any function which satisfies the given equation. Linear Homogeneous Recurrence Relations with Constant Coefficients:The equation is said to be linear homogeneous difference equation if and only if R (n) = 0 and it will be of order n. The equation is said to be linear non-homogeneous difference equation if R (n) ≠ 0. Example1: The equation ar+3+6ar+2+12ar+1+8ar=0 is a linear non-homogeneous equation of order 3. Example2: The equation ar+2-4ar+1+4ar= 3r + 2r is a linear non-homogeneous equation of order 2. A linear homogeneous difference equation with constant coefficients is given by C0 yn+C1 yn-1+C2 yn-2+⋯......+Cr yn-r=0 ....... equation (i) Where C0,C1,C2.....Cn are constants. The solution of the equation (i) is of the form Substitute the values of A ∝K for yn in equation (1), we have C0 A∝K+C1 A∝K-1+C2 A∝K-2+⋯....+Cr A∝K-r=0.......equation (ii) After simplifying equation (ii), we have C0 ∝r+C1 ∝r-1+C2 ∝r-2+⋯Cr=0..........equation (iii) The equation (iii) is called the characteristics equation of the difference equation. If ∝1 is one of the roots of the characteristics equation, then To find the solution of the linear homogeneous difference equations, we have the four cases that are discussed as follows: Case1: If the characteristic equation has n distinct real roots∝1, ∝2, ∝3,.......∝n. Thus, Also, we have Hence, the homogeneous solutions of the difference equation are 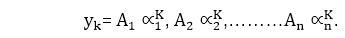
Case2: If the characteristics equation has repeated real roots. If ∝1=∝2, then (A1+A2 K) If ∝1=∝2=∝3 then (A1+A2 K+A3 K2) Similarly, if root ∝1 is repeated n times, then. (A1+A2 K+A3 K2+......+An Kn-1) The solution to the homogeneous equation. Case3: If the characteristics equation has one imaginary root. If α+iβ is the root of the characteristics equation, then α-iβ is also the root, where α and β are real. Thus, (α+iβ)K and (α-iβ)K are solutions of the equations. This implies (α+iβ)K A1+α-iβ)K A2 Is also a solution to the characteristics equation, where A1 and A2 are constants which are to be determined. Case4: If the characteristics equation has repeated imaginary roots. When the characteristics equation has repeated imaginary roots, (C1+C2 k) (α+iβ)K +(C3+C4 K)(α-iβ)K Is the solution to the homogeneous equation. Example1: Solve the difference equation ar-3ar-1+2ar-2=0. Solution: The characteristics equation is given by s2-3s+2=0 or (s-1)(s-2)=0⇒ s = 1, 2 Therefore, the homogeneous solution of the equation is given by ar=C1r+C2.2r.Example2: Solve the difference equation 9yK+2-6yK+1+yK=0. Solution: The characteristics equation is 9s2-6s+1=0 or (3s-1)2=0⇒ s = 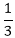 and and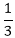
Therefore, the homogeneous solution of the equation is given by Example3: Solve the difference equation yK-yK-1-yK-2=0. Solution: The characteristics equation is s2-s-1=0 Therefore, the homogeneous solution of the equation is 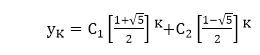
Example4: Solve the difference equation yK+4+4yK+3+8yK+2+8yK+1+4yK=0. Solution: The characteristics equation is s4+4s3+8s2+8s+4=0 Therefore, the homogeneous solution of the equation is given by yK=(C1+C2 K)(-1+i)K+(C3 +C4 K)(-1-i)K
Next TopicParticular Solution
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





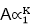 , where ∝1 is the characteristics root and A is constant.
, where ∝1 is the characteristics root and A is constant. 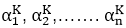 are all solutions of equation (i).
are all solutions of equation (i).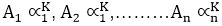 are all solutions of equation (i). The sums of solutions are also solutions.
are all solutions of equation (i). The sums of solutions are also solutions.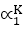 is also a solution.
is also a solution.