Discrete Mathematics
Sets Theory
Sets Introduction
Types of Sets
Sets Operations
Algebra of Sets
Multisets
Inclusion-Exclusion Principle
Mathematical Induction
Relations
Binary Relation
Representation of Relations
Composition of Relations
Types of Relations
Closure Properties of Relations
Equivalence Relations
Partial Ordering Relations
Functions & Algorithms
Functions
Types of Functions
Identity Functions
Composition of Functions
Mathematical Functions
Algorithms & Functions
Logic & Propositional
Propositions & Compound Statements
Basic Logical Operations
Conditional & Biconditional Statements
Tautologies & Contradictions
Predicate Logic
Normal Forms
Counting Techniques
Recurrence Relations
Recurrence Relations
Linear Recurrence Relations with Constant Coefficients
Particular Solution
Total Solution
Generating Functions
Probability Theory
Graph Theory
Introduction of Graphs
Types of Graphs
Representation of Graphs
Isomorphic and Homeomorphic Graphs
Regular and Bipartite Graphs
Planar and Non-Planar Graphs
Dijkstra's Algorithm
Travelling Salesman Problem
Binary Trees
Introduction of Trees
Binary Trees
Traversing Binary Trees
Binary Search Trees
Minimum Spanning Tree
Operator & Postulates
Group Theory
Ordered Sets & Lattices
Boolean Algebra
Misc
Proof of De Morgan's Law
Discrete mathematics for Computer Science
Abelian Groups in Discrete Mathematics
Applications of Discrete Mathematics in Computer Science
Rings in Discrete Mathematics
Order of Group in Discrete Mathematics
Principle of Duality in Discrete Mathematics
Atomic Propositions in Discrete Mathematics
Applications of Tree in Discrete Mathematics
Quantifiers
Algebraic Structure
Counting principle
Bijective Function in Discrete Mathematics
Multinomial Theorem
Lagrange's Mean Value Theorem
Cauchy's Mean Value Theorem
Rolle's Mean Value Theorem
Semantic difference between Set and Type
Application of Group Theory in Discrete Mathematics
Directed and Undirected graph in Discrete Mathematics
Bayes Formula for Conditional probability
Difference between Function and Relation in Discrete Mathematics
Recursive functions in discrete mathematics
Arguments in Discrete Mathematics
Elementary Matrix in Discrete Mathematics
Hypergeometric Distribution in Discrete Mathematics
Regular Grammar in Discrete Mathematics
Prime Number in Discrete Mathematics
Peano Axioms Number System Discrete Mathematics
Problems of Monomorphism and Epimorphism in Discrete mathematics
Properties of Set in Discrete mathematics
Principal Ideal Domain in Discrete mathematics
Probable error formula for discrete mathematics
HyperGraph & its Representation in Discrete Mathematics
Hashing Function in Discrete mathematics
Doolittle Algorithm: LU Decomposition
RSA Encryption in Discrete Mathematics
Introduction to Mojette Transform
Negation in Discrete mathematics
Hamiltonian Graph in Discrete mathematics
Relationship between number of nodes and height of binary tree
Independent events in Probability
Repeated Trials in probability
Betweenness Centrality
Inference theory in discrete mathematics
Tautology in Discrete Mathematics
Walks, Trails, Path, Circuit and Cycle in Discrete mathematics
Associative Law in Discrete Mathematics
Conjunction in Discrete Mathematics
Distributive Law of Multiplication
Proof by Contradiction in Discrete mathematics
Chromatic Number of graphs
How to find Chromatic Number
Chromatic Polynomial in Discrete mathematics
Identity Function in Discrete mathematics
Injective Function in Discrete mathematics
Many to one function in Discrete Mathematics
Surjective Function in Discrete Mathematics
Inverse Function in Discrete mathematics
Sampling and Inference
Constant Function in Discrete Mathematics
Graphing Functions in Discrete mathematics
Continuous Functions in Discrete mathematics
Linear Function in Discrete mathematics
Complement of Graph in Discrete mathematics
Graph isomorphism in Discrete Mathematics
Euler Graph in Discrete Mathematics
Planer Graph in Discrete Mathematics
Bipartite Graph in Discrete mathematics
Handshaking Theory in Discrete mathematics
Konigsberg Bridge Problem in Discrete mathematics
What is Incidence matrix in Discrete mathematics
Implication in Discrete mathematics
Incident coloring in Discrete mathematics
Biconditional Statement in Discrete Mathematics
In-degree and Out-degree in discrete mathematics
Law of Logical Equivalence in Discrete Mathematics
Graph theory in Discrete Mathematics
Discrete Infinite Groups
Independent set in discrete mathematics
Inverse of a Matrix in Discrete mathematics
Inverse property in Discrete mathematics
Irrational Number in Discrete mathematics
Linear Graph in Discrete Mathematics
Difference between the Linear equations and Non-linear equations
Lagrange Theorem in Discrete mathematics
Linear Equations in Discrete mathematics
Limitation and Propositional Logic and Predicates
Non-linear Function in Discrete mathematics
Lexicographic Orders
Graph Measurements in Discrete Mathematics
Language and Grammar in Discrete mathematics
Logical Connectives in Discrete mathematics
Propositional Logic in Discrete mathematics
Conditional and Bi-conditional connectivity
Problems based on Converse, inverse and Contrapositive
Nature of Propositions in Discrete mathematics
PDNF and PCNF in Discrete Mathematics
Linear Correlation in Discrete mathematics
Equivalence of Formula in Discrete mathematics
Discrete time signals in Discrete Mathematics
M-array Tree in Discrete Mathematics
Matrix in Discrete mathematics
Type of matrices in Discrete mathematics
Column matrix in discrete mathematics
Zero matrix in Discrete mathematics
Rectangular matrix in Discrete mathematics
Row matrix in Discrete mathematics
Square matrix in discrete mathematics
Diagonal matrix in Discrete mathematics
Singular matrix in Discrete mathematics
Non-singular matrix in Discrete mathematics
Order of matrix in Discrete mathematics
Hermitian matrix in Discrete mathematics
Skew-Hermitian matrix in Discrete mathematics
Skew-symmetric matrix in Discrete mathematics
Symmetric Matrix in Discrete mathematics
Orthogonal matrix in Discrete mathematics
Determinants in Discrete mathematics
DMS MCQ
Identity FunctionsThe function f is called the identity function if each element of set A has an image on itself i.e. f (a) = a ∀ a ∈ A. It is denoted by I. Example: The function f is an identity function as each element of A is mapped onto itself. The function f is a one-one and onto 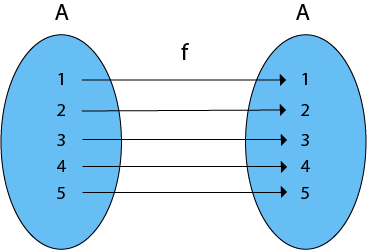
Invertible (Inverse) FunctionsA function f: X → Y is invertible if and only if it is a bijective function. Consider the bijective (one to one onto) function f: X → Y. As f is a one to one, therefore, each element of X corresponds to a distinct element of Y. As f is onto, there is no element of Y which is not the image of any element of X, i.e., range = co-domain Y. The inverse function for f exists if f-1 is a function from Y to X. Example: 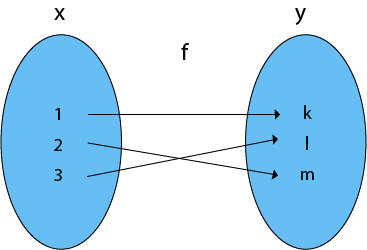
The inverse function of f is shown in fig: 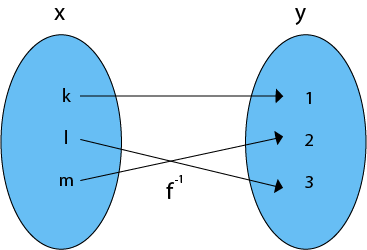
Next TopicComposition of Functions
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










