In-degree and Out-degree in discrete mathematicsTo understand the in-degree and out-degree of a vertex, we have to first learn about the concept of degree of a vertex. After that, we can easily understand the in-degree and out-degree of a vertex. We should know that the in-degree and out-degree can only be determined in the directed graph. We can calculate the degree of a vertex with the help of an undirected graph. In the undirected graph, we cannot calculate the in-degree and out-degree of a vertex. Degree of a vertexIf we want to find the degree of each vertex in a graph, in this case, we have to count the number of relations that are established by a particular vertex with the other vertex. In other words, we can determine the degree of a vertex with the help of calculating the number of edges connecting to that vertex. The degree of a vertex is indicated with the help of deg(v). If there is a simple graph, which contains n number of vertices, in this case, the degree of any vertex will be: A vertex has the ability to form an edge with all other vertices in a graph except by itself. So in a simple graph, the degree of a vertex will find out by the number of vertices in a graph minus 1. Here 1 is used for the self vertex because it does not make a loop by itself. If the graph contains the vertices which have the self-loop, then that type of graph will not be a simple graph. Example: In this example, we have a graph that has 6 vertices, i.e., a, b, c, d, e, and f. The vertex 'a' has degree 5, and all the other vertices have a degree 1. If any vertex has degree 1, then that type of vertex will be known as the 'end vertex'. 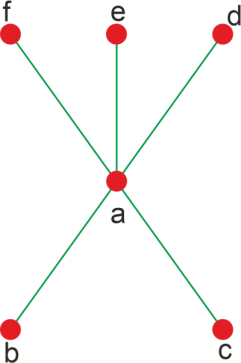
There are two cases of graphs in which we can consider the degree of a vertex, which are described as follows:
Now we will learn the degree of a vertex in a directed graph and the degree of a vertex in an undirected graph in detail. Degree of a vertex in an Undirected graph If there is an undirected graph, then in this type of graph, there will be no directed edge. The examples to determine the degree of a vertex in an undirected graph are described as follows: Example 1: In this example, we will consider an undirected graph. Now we will find out the degree of each vertex in that graph. 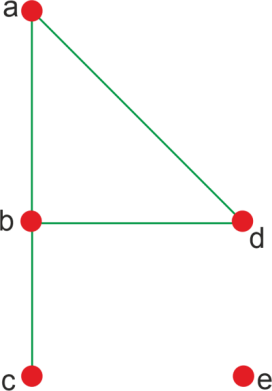
Solution: In the above-undirected graph, there are total 5 numbers of vertices, i.e., a, b, c, d, and e. The degree of each vertex is described as follows:
Example 2: In this example, we will consider an undirected graph. Now we will find out the degree of each vertex in that graph. 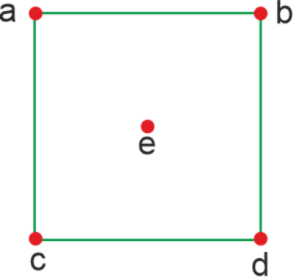
Solution: In the above undirected graph, there are total 5 numbers of vertices, i.e., a, b, c, d, and e. The degree of each vertex is described as follows: Degree of vertex a = deg(a) = 2 Degree of vertex b = deg(b) = 2 Degree of vertex c = deg(c) = 2 Degree of vertex d = deg(d) = 2 Degree of vertex e = deg(e) = 0 In this graph, there is no pendent vertex, and vertex 'e' is an isolated vertex. Degree of vertex in Directed graphIf the graph is a directed graph, then in this graph, each vertex must have an in-degree and out-degree. Suppose there is a directed graph. In this graph, we can use the following steps to find out the in-degree, out-degree, and degree of a vertex. In-degree of a vertex The in-degree of a vertex can be described as a number of edges with v, where v is used to indicate the terminal vertex. In other words, we can describe it as a number of edges coming to the vertex. With the help of syntax deg-(v), we can write the in-degree of a vertex. If we want to determine the in-degree of a vertex, for this, we have to count the number of edges that ends at the vertex. Out-degree of a vertex The out-degree of a vertex can be described as a number of edges with v, where v is used to indicate the initial vertex. In other words, we can describe it as a number of edges coming out from the vertex. With the help of syntax deg+(v), we can write the out-degree of a vertex. If we want to determine the out-degree of a vertex, for this, we have to count the number of edges that begins from the vertex. Degree of a vertex The degree of a vertex is indicated with the help of deg(v), which is equal to the addition of in-degree of a vertex and out-degree of a vertex. The symbolic representation of degree of a vertex is described as follows: Example 1: In this example, we have a graph, and we have to determine the degree of each vertex. 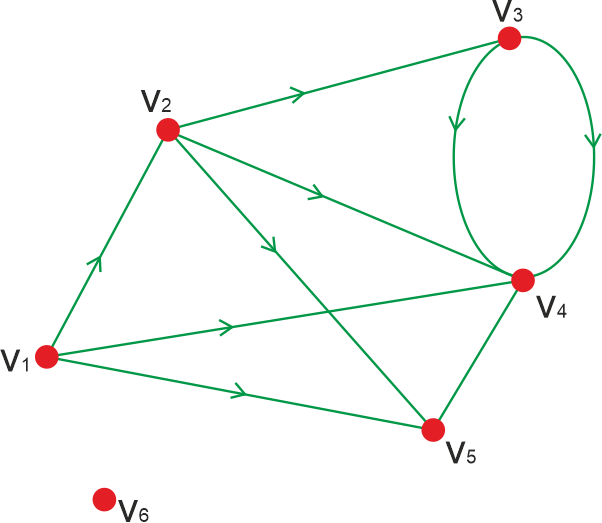
Solution: For this, we will first find out the degree of a vertex, in-degree of a vertex and then the out-degree of a vertex. As we can see that the above graph contains the total 6 vertex, i.e., v1, v2, v3, v4, v5 and v6. In-degree: In-degree of a vertex v1 = deg(v1) = 1 In-degree of a vertex v2 = deg(v2) = 1 In-degree of a vertex v3 = deg(v3) = 1 In-degree of a vertex v4 = deg(v4) = 5 In-degree of a vertex v5 = deg(v5) = 1 In-degree of a vertex v6 = deg(v6) = 0 Out-degree: Out-degree of a vertex v1 = deg(v1) = 2 Out-degree of a vertex v2 = deg(v2) = 3 Out-degree of a vertex v3 = deg(v3) = 2 Out-degree of a vertex v4 = deg(v4) = 0 Out-degree of a vertex v5 = deg(v5) = 2 Out-degree of a vertex v6 = deg(v6) = 0 Degree of a vertex With the help of the definition described above, we know that the degree of a vertex Deg(v) = deg-(v) + deg+(v). Now we will calculate it with the help of this formula like this: Degree of a vertex v1 = deg(v1) = 1+2 = 3 Degree of a vertex v2 = deg(v2) = 1+3 = 4 Degree of a vertex v3 = deg(v3) = 1+2 = 3 Degree of a vertex v4 = deg(v4) = 5+0 = 5 Degree of a vertex v5 = deg(v5) = 1+2 = 3 Degree of a vertex v6 = deg(v6) = 0+0 = 0 Example 2: In this example, we have a directed graph with 7 vertices. The vertex 'a' contains 2 edges, i.e., 'ad' and 'ab', which are going outwards. Hence, vertex 'a' contains the out-degree, which is 2. Similarly, the vertex 'a' also has an edge 'ga', which is coming toward this vertex 'a'. Hence, the vertex 'a' contains the in-degree, which is 1. 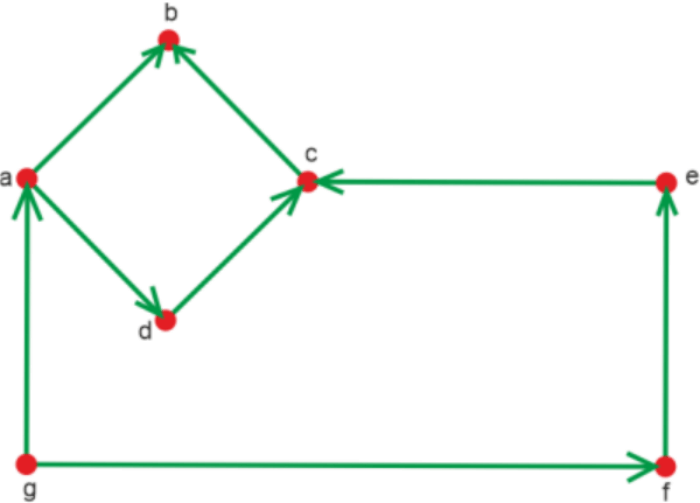
Solution: The in-degree and out-degree of all the above vertices are described as follows: In-degree: In-degree of a vertex a = deg(a) = 1 In-degree of a vertex b = deg(b) = 2 In-degree of a vertex c = deg(c) = 2 In-degree of a vertex d = deg(d) = 1 In-degree of a vertex e = deg(e) = 1 In-degree of a vertex f = deg(f) = 1 In-degree of a vertex g = deg(g) = 0 Out-degree: Out-degree of a vertex a = deg(a) = 2 Out-degree of a vertex b = deg(b) = 0 Out-degree of a vertex c = deg(c) = 1 Out-degree of a vertex d = deg(d) = 1 Out-degree of a vertex e = deg(e) = 1 Out-degree of a vertex f = deg(f) = 1 Out-degree of a vertex g = deg(g) = 2 Degree of each vertex: We known that the degree of a vertex Deg(v) = deg-(v) + deg+(v). Now we will calculate it with the help of this formula like this: Degree of a vertex a = deg(a) = 1+2 = 3 Degree of a vertex b = deg(b) = 2+0 = 2 Degree of a vertex c = deg(c) = 2+1 = 3 Degree of a vertex d = deg(d) = 1+1 = 2 Degree of a vertex e = deg(e) = 1+1 = 2 Degree of a vertex f = deg(f) = 1+1 = 2 Degree of a vertex g = deg(g) = 0+2 = 2 Example 3: In this example, we have a directed graph with 5 vertices. The vertex 'a' contains 1 edge, i.e., 'ae', which are going outwards. Hence, vertex 'a' contains an out-degree, which is 1. Similarly, the vertex 'a' also has an edge 'ba', which is coming toward this vertex 'a'. Hence, the vertex 'a' contains the in-degree, which is 1. 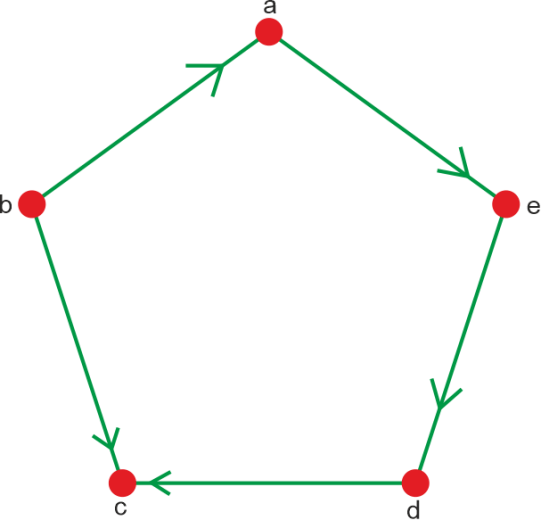
Solution: The in-degree and out-degree of all the above vertices are described as follows: In-degree In-degree of a vertex a = deg(a) = 1 In-degree of a vertex b = deg(b) = 0 In-degree of a vertex c = deg(c) = 2 In-degree of a vertex d = deg(d) = 1 In-degree of a vertex e = deg(e) = 1 Out-degree: Out-degree of a vertex a = deg(a) = 1 Out-degree of a vertex b = deg(b) = 2 Out-degree of a vertex c = deg(c) = 0 Out-degree of a vertex d = deg(d) = 1 Out-degree of a vertex e = deg(e) = 1 Degree of each vertex: We known that the degree of a vertex Deg(v) = deg-(v) + deg+(v). Now we will calculate it with the help of this formula like this: Degree of a vertex a = deg(a) = 1+1 = 2 Degree of a vertex b = deg(b) = 0+2 = 2 Degree of a vertex c = deg(c) = 2+0 = 2 Degree of a vertex d = deg(d) = 1+1 = 2 Degree of a vertex e = deg(e) = 1+1 = 2 Example 4: In this example, we have a graph, and we have to determine the degree, in-degree, and out-degree of each vertex. 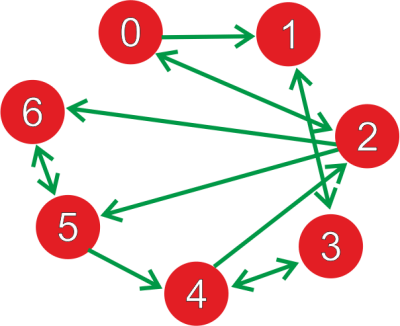
Solution: For this, we will first find out the in-degree of a vertex and then the out-degree of a vertex. As we can see that the above graph contains the total 8 vertex, i.e., 0, 1, 2, 3, 4, 5, and 6. In-degree: In-degree of a vertex 0 = deg(0) = 1 In-degree of a vertex 1 = deg(1) = 2 In-degree of a vertex 2 = deg(2) = 2 In-degree of a vertex 3 = deg(3) = 2 In-degree of a vertex 4 = deg(4) = 2 In-degree of a vertex 5 = deg(5) = 2 In-degree of a vertex 6 = deg(6) = 2 Out-degree: Out-degree of a vertex 0 = deg(0) = 2 Out-degree of a vertex 1 = deg(1) = 1 Out-degree of a vertex 2 = deg(2) = 3 Out-degree of a vertex 3 = deg(3) = 2 Out-degree of a vertex 4 = deg(4) = 2 Out-degree of a vertex 5 = deg(5) = 2 Out-degree of a vertex 6 = deg(6) = 1 Degree of each vertex: We known that the degree of a vertex Deg(v) = deg-(v) + deg+(v). Now we will calculate it with the help of this formula like this: Degree of a vertex 0 = deg(0) = 1+2 = 3 Degree of a vertex 1 = deg(1) = 2+1 = 3 Degree of a vertex 2 = deg(2) = 2+3 = 5 Degree of a vertex 3 = deg(3) = 2+2 = 4 Degree of a vertex 4 = deg(4) = 2+2 = 4 Degree of a vertex 5 = deg(5) = 2+2 = 4 Degree of a vertex 6 = deg(5) = 2+1 = 3 Degree sequence of a GraphTo determine the degree sequence of a graph, we have to first determine the degree of each vertex in a graph. After that, we will write these degrees in ascending order. This order/sequence can be called the degree sequence of a graph. For example: In this example, we have three graphs that have 3, 4, and 5 vertices, and the degree sequence of all the graphs is 3. 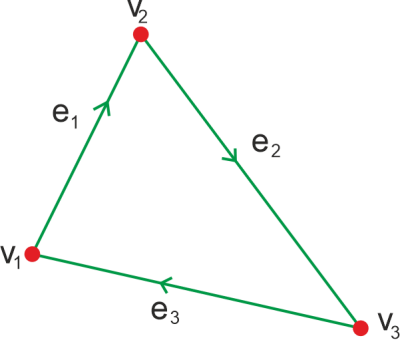
In the above graph, there are 3 vertices. The degree of a sequence of this graph is described as follows: <2, 2, 2> 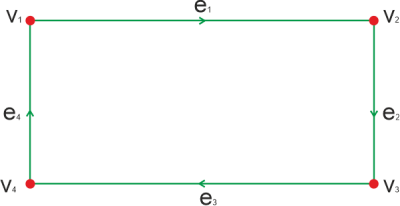
In the above graph, there are 4 vertices. The degree sequence of this graph is described as follows: <2, 2, 2, 2> 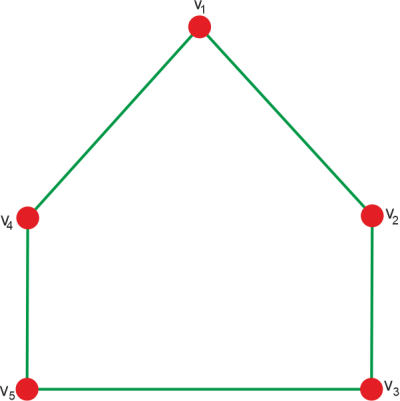
In the above graph, there are 5 vertices. The degree sequence of this graph is described as follows: <2, 2, 2, 2, 2> |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









