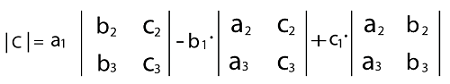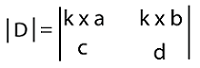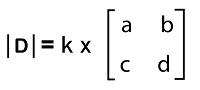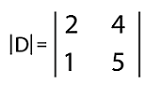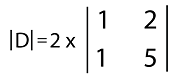Determinants in Discrete mathematics

Determinants can be described as the scalar quantities which will be obtained when we add the products of elements of a square matrix and their cofactors on the basis of a prescribed rule. With the help of determinant, we will be able to determine the adjoint, inverse of the matrix, and many more. In case of the determinant, horizontal lines are used to indicate the rows, and vertical lines are used to indicate the columns. If there is a determinant with n order, in this case, it will have n rows and m columns.

For example: Suppose there are two matrices, which are described as follows: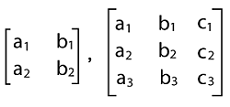

The determinant of this matrix is described as follows: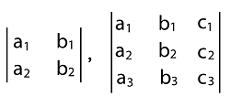

In this example, we have two determinants in which the first determinant contains the 2 order and the second determinant contains the 3 order. If there is a square matrix A with an order n*n, in this case, there must be a number associated with it which will be known as the determinant of a square matrix. For example:

1. If there is a matrix with an order of 1*1, then the determinant of it will be A = [a].

2. Suppose there is a matrix with an order 2*2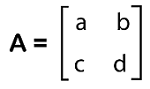

The determinant of this 2*2 matrix will be ad - bc.

3. Suppose there is a matrix with an order 3*3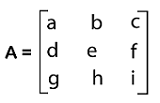

The determinant of this matrix will be a(ei − fh) − b (di − fg) + c (dh − eg).

Note: If there is a determinant with an order n, then the number of elements will be n².

What are Determinants

The determinants can be described as a scaling factor of matrices. This matrix can be considered as a function that is used to shrink in and stretch out of the matrices. Just like the function, determinants take a square matrix in the form of input and return a single number in the form of its output.

Definition of Determinants

Suppose there is a square matrix, C = [cij] with an order n*n. The determinant of this matrix can be defined as a scalar value that is used to have a real or complex number. Here cij is used to indicate the (i, j)th element of matrix C. The determinant of matrix C will be indicated as |C| or det(C). We use the grid of numbers to write the determinants and arrange these numbers inside absolute value bars in place of using square brackets.

For example: Suppose there is a matrix C where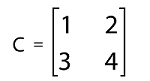

The determinant of this matrix can be written in the following way: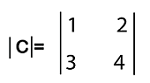

How to calculate determinant

If there is a simple square matrix with an order 1*1, in this case, the matrix will have only one number, and the determinant of this matrix will be the number itself. Now we will see the matrix with 2-order, 3-order and 4-order, and how we can calculate the determinants of these matrices.

Calculating determinant of 2*2 matrix

There is a determinant formula that can be used to determine the determinant of any 2D square matrix or any square matrix which contains the 2*2 order. For this, we will assume a square matrix with 2*2 order: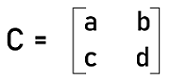

In the following way, we can calculate the determinant of 2*2 matrix or 2D determinant: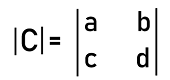

|C| = (a*d - b*c)

For example: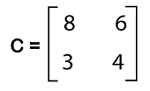

Now we will calculate its determinant in the following way: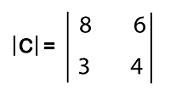

|C| = (8*4) - (6*3)

|C| = 32 - 18

|C| = 14

Calculating determinant of 3*3 matrix

We have a determinant formula that will be useful to calculate the determinant of a 3*3 square matrix. Suppose there is a square matrix that contains the 3*3 order: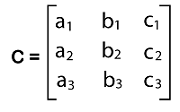

In the following way, we can show the determinant of this matrix: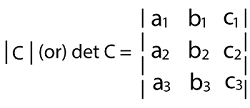

We can calculate the determinant of a 3*3 matrix with the help of some steps, which are described as follows:

• In the above matrix, a1 is fixed in the form of an anchor number and the 2*2 determinant of its sub-matrix (minor of a1).
• In the same way, we can find the minor of b1 and c1.
• Now we will keep multiplying the small determinant of the matrix by the anchor number and by its sign in the following way:
  
• In the last step, we will add them up in the following way:
  
  |C| = a1(b2c3 - b3c2) - b1(a2c3 - a3c2) + c1(a2b3 - a3b2)

Now we will understand it with the help of an example. Suppose we have a 3*3 matrix B where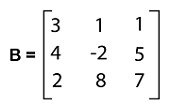

Now we will calculate the determinant of this matrix in the following way: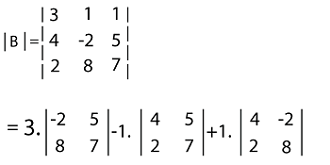

= 3 × ((-2)(7) - (5)(8)) -1 × ((4)(7) - (5)(2)) + 1 × ((4)(8) - (-2)(2))

= 3 × ((-14) - (40)) -1 × ((28) - (10)) + 1 × ((32) - (-4))

= 3 × (-54) -1 × (18) + 1 × (36)

= - 162 - 18 + 36

= -144

In this example, we use the first row to find the determinant of a 3*3 matrix. But we can also use any row or column to determine the determinants of this matrix.

Note: In conclusion, we can say that the formula to determine the determinant of a 3*3 matrix is described as follows: |C| = a1(b2c3 - b3c2) - b1(a2c3 - a3c2) + c1(a2b3 - a3b2)

Calculating Determinant of 4*4 matrix

Suppose there is a square matrix that contains the order 4*4 or a 4D square matrix. When we try to calculate the determinant of a 4*4 matrix, then there are some changes that we should keep in mind. The 4*4 matrix and the changes are described as follows:

• If we delete the row and column containing the element a1, we can get the determinant of 3*3 matrix plus a1 times.
• If we delete the row and column containing the element b1, we can get the determinant of 3*3 matrix minus b1 times.
• If we delete the row and column containing the element c1, we can get the determinant of 3*3 matrix plus c1 times.
• If we delete the row and column containing the element d1, we can get the determinant of 3*3 matrix minus d1 times.

We can also use the method which we already learned in the above topic, i.e., "calculating determinant of 3*3 matrix" to find the determinant of 3*3 matrix. Here we will show a very easy way through which we can find the determinant of 3*3 matrix, which is described as follows:

Multiplication of Determinants

We can multiply the two determinants of square matrices with the help of using a method which is known as multiplication of arrays. Now we will multiply two determinants of square matrices, A and B, of different orders with the help of row by column multiplication rule.

Multiplication of 2*2 determinants

Here we will assume two square matrices, A and B, which contain the order 2*2. We can indicate the determinants of these matrices by the symbol |A| and |B|, respectively. The procedure to multiply these determinants is described as follows:

Multiplication of 3*3 determinants

Here we will assume two square matrices, C and D, which contain the order 3*3. We can indicate the determinants of these matrices by the symbol |C| and |D|, respectively. The procedure to multiply these determinants is described as follows:

When we try to multiply two determinants, then there are some points that we should keep in mind. These points are described as follows:

• We can multiply two determinants if and only if both the determinants contain the same order.
• If we interchange the rows and columns, in this case, the values of determinants will not be changed. Because of this reason, we can multiply two determinants with the help of following the multiplication rules of a column by column, row by row, or column by row.

Properties of Determinants

Suppose there are some square matrices with different types. If we try to calculate its determinant, there are some important properties of determinants that should be followed to do this. We have listed the important properties of determinants, and some of them are described as follows:

Property 1: "If there is an identity matrix, then its determinant will always be 1".

Proof: For this, we will assume an identity matrix I where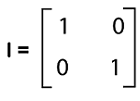

The determinant of this matrix is described as follows:

|I| = (1)(1) - (0)(0) = 1

Hence, the determinant of any identity matrix will always be 1.

Property 2: "If there is a square matrix B, which contains the order n*n, and if this matrix contain a 0 row and 0 column, then the determinant of this matrix will be 0, i.e., det(B) = 0".

Proof: For this, we will assume the determinant of a square matrix B like this: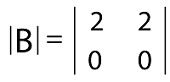

|B| = (2)(0) - (2)(0) = 0.

In the above square matrix B, we have one 0 row. Hence the determinant of matrix B will be 0.

Property 3: "If there is a matrix C which is an upper or lower triangular matrix, then the determinant of this matrix will be the multiplication of all its diagonal entries".

Proof: For this, we will assume an upper triangular matrix C, which contains 3, 2, and 4 as their diagonal entries. The determinant of matrix C is described as follows: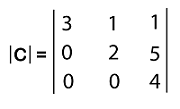

|C| = 3*2*4 = 24

Hence the determinant of C will be 24.

Property 4: If there is a square matrix, and if the row of this matrix is multiplied by a constant k, in this case, the constant k will be taken out of the determinant.

Proof:

|D| = (2)(5) - (4)(1) |D| = 10 - 4 = 6	|D| = 2* {(1)(5) - (2)(1)} |D| = 2* (5-2) =2*3 = 6

In both matrices, we can see that the determinant remains the same.

There are some other important properties of determinant, which is described as follows:

• If there is a square matrix, then it will be known as invertible iff det(C) ≠ 0.
• If there are two square matrices, A and B which contains the order n*n, in this case, det(BC) = det(B) * det(C) = det(C) * det(B).
• We can indicate the relationship between a matrix D's determinant and its adjoint in the following way: D * adj(D) = adj(D) * D = |D| * I. Here I is used to indicate the identity matrix, and D is used to indicate the square matrix.

Rules for operations on Determinant

If we try to perform the rows and columns operations, then there are some rules which will be useful. These rules are described as follows:

• If we change the rows into columns and columns into rows, in this case, the value of determinant will not be changed.
• If we interchange any two rows or two columns, in this case, the sign of determinant will not be changed.
• The value of determinant of the given matrix will be 0 if and only if any two rows or columns are the same.
• If there is a constant in the matrix that is multiplied by every element of a particular row or column of that matrix, in this case, the constant will also be multiplied by the value of determinant.
• If each and every element of a row or column is expressed in the form of a sum of elements, in this case, the determinant will also be expressed in the form of a sum of determinants.
• If the value of determinant will not be changed if we add or subtract the elements of a row or column with corresponding multiples of elements of another row or column.

Important Notes on Determinants

There are some important points that we should keep in mind while learning the concept of determinants. These points are described as follows:

• We can consider determinant as a function. That means it can take a square matrix in the form of input and return a single number in the form of output.
• A matrix will be known as a square matrix if it contains the same number of rows and columns.
• If there is a simplest square matrix with an order 1*1, then the determinant of this matrix will be the number itself because the 1*1 matrix contains only one number.

Examples of Determinants

There are a lot of examples of determinants, and some of them are described as follows:

Example 1: In this example, we have a matrix A, and we have to determine the determinant of this matrix. The elements of this matrix are described as follows: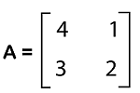

Solution: The determinant of the above matrix can be written in the following way: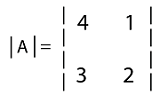

Now we will determine the determinant of it by multiplying the diagonals and subtracting the products in the following way:

|A| = (4*2) - (3*1)

= 8 - 3

= 5

Answer: det(A) or |A| = 5

Example 2: In this example, we have a matrix C with 2*2 order, and we have to determine the determinant of this matrix. The elements of this matrix are described as follows: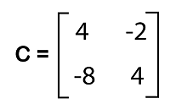

Solution: The determinant of the above 2*2 matrix can be written in the following way: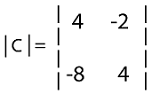

Now we will determine the determinant of it in the following way:

|C| = {(4)(4) - (8)(2)}

= 16-16

= 0

Answer: The determinant of matrix C is = 0.

Example 3: In this example, we have a matrix A with 3*3 order, and we have to determine the determinant of this matrix. The elements of this matrix are described as follows: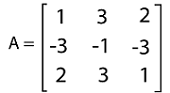

Solution: Here, we will use the first row and expand the determinant of above 3*3 matrix.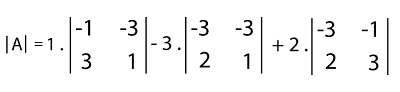

= 1 * (-1 - (-9) - 3 * (-3 - (-6) + 2 * (-9 - (-2))

= 1* (-1 + 9) - 3* (-3 + 6) + 2 * (-9 + 2)

= 8 - 9 - 14

= -15

Answer: The determinant of matrix A is -15.

Example 4: In this example, we have to determine the value of determinant with the help of properties of determinants. The determinant is described as follows: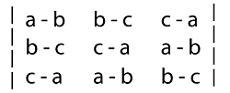

Solution: With the help of one of the properties of determinant, we will perform the elementary row transformation R₁ → R₁ + R₂ + R₃ on the above determinant. According to this property, the value of determinants will not be changed while doing the elementary row transformation. After performing the elementary row transformation (R₁ → R₁ + R₂ + R₃), the determinant will become the following: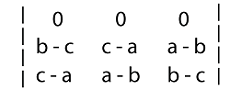

Now we will use one more property of determinant that says if the row or column of a matrix is 0, then the determinant of this matrix will also be 0. In the above matrix, the first row is 0. That's why the value of above determinant is 0.

Answer: The value of determinant is 0.