Hamiltonian Graph in Discrete mathematics

The graph will be known as a Hamiltonian graph if there is a closed walk in a connected graph, which passes each and every vertex of the graph exactly once except the root vertex or starting vertex. The Hamiltonian walk must not repeat any edge. One more definition of a Hamiltonian graph says a graph will be known as a Hamiltonian graph if there is a connected graph, which contains a Hamiltonian circuit. The vertex of a graph is a set of points, which are interconnected with the set of lines, and these lines are known as edges. The example of a Hamiltonian graph is described as follows: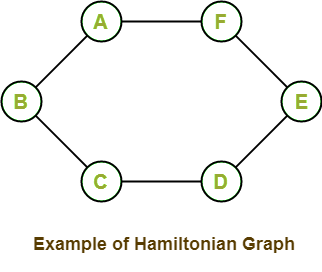

• In the above graph, there is a closed walk ABCDEFA.
• Except for the starting vertex, it passed through every vertex of the graph exactly once.
• At the time of walk, the edges are not repeating.
• Due to all the reasons, we can say that this graph is a Hamiltonian graph.

In other words, we can say that the above graph contains a Hamiltonian circuit. That's why this graph is a Hamiltonian graph.

Hamiltonian Path

In a connected graph, if there is a walk that passes each and every vertex of a graph only once, this walk will be known as the Hamiltonian path. In this walk, the edges should not be repeated. There is one more definition to describe the Hamiltonian path: if a connected graph contains a Path with all the vertices of the graph, this type of path will be known as the Hamiltonian path.

Examples of Hamiltonian Path

There are a lot of examples of the Hamiltonian path, which are described as follows:

Example 1: In the following graph, we have 5 nodes. Now we have to determine whether this graph contains a Hamiltonian path.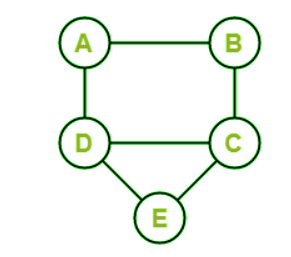

Solution:

In the above graph, we can see that when we start from A, then we can go to B, C, D, and then E. So this is the path that contains all the vertices (A, B, C, D, and E) only once, and there is no repeating edge. That's why we can say that this graph has a Hamiltonian path, which is described as follows:

Hamiltonian path = ABCDE

Example 2: In the following graph, we have 5 nodes. Now we have to determine whether this graph contains a Hamiltonian path.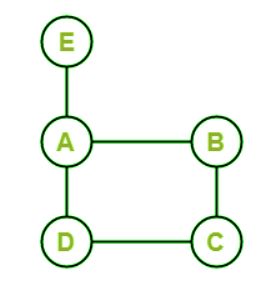

Solution:

In the above graph, we can see that when we start from the E, then we can go to A, B, C, and then D. So this is the path that contains all the vertices (A, B, C, D, and E) only once, and there is no repeating edge. That's why we can say that this graph has a Hamiltonian path, which is described as follows:

Hamiltonian path = EABCD

Example 3: In the following graph, we have 5 nodes. Now we have to determine whether this graph contains a Hamiltonian path.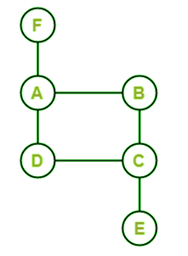

Solution:

In the above graph, we can see that there is no path that covers all the vertices (A, B, C, D, and E) only once. If we start from F, then we will go to A, B, C. After C, we can either go to D or F, but we cannot go to both the vertices. That's why we can say that this graph does not contain a Hamiltonian path.

Hamiltonian Circuit

In a connected graph, if there is a walk that passes each and every vertex of the graph only once and after completing the walk, return to the starting vertex, then this type of walk will be known as a Hamiltonian circuit. For the Hamiltonian circuit, there must be no repeated edges. We can also be called Hamiltonian circuit as the Hamiltonian cycle.

There are some more definitions of the Hamiltonian circuit, which are described as follows:

• If there is a Hamiltonian path that begins and ends at the same vertex, then this type of cycle will be known as a Hamiltonian circuit.
• In the connected graph, if there is a cycle with all the vertices of the graph, this type of cycle will be known as a Hamiltonian circuit.
• A closed Hamiltonian path will also be known as a Hamiltonian circuit.

Examples of Hamiltonian Circuit

There are a lot of examples of the Hamiltonian circuit, which are described as follows:

Example 1: In the following graph, we have 5 nodes. Now we have to determine whether this graph contains a Hamiltonian circuit.

Solution: =

The above graph contains the Hamiltonian circuit if there is a path that starts and ends at the same vertex. So when we start from the A, then we can go to B, C, E, D, and then A. So this is the path that contains all the vertices (A, B, C, D, and E) only once, except the starting vertex, and there is no repeating edge. That's why we can say that this graph has a Hamiltonian circuit, which is described as follows:

Hamiltonian circuit = ABCDEA

Example 2: In the following graph, we have 5 nodes. Now we have to determine whether this graph contains a Hamiltonian circuit.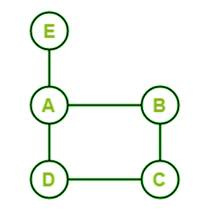

Solution:

The above graph contains the Hamiltonian circuit if there is a path that starts and ends at the same vertex. So we will start from the E, then we can go A, B, C, D. To react to the same vertex E, we can have to again go to vertex A. So this is the path that contains all the vertices (A, B, C, D, and E), but vertex A is repeated to reach the initial vertex. That's why we can say that this graph does not contain a Hamiltonian circuit.

Example 3: In the following graph, we have 6 nodes. Now we have to determine whether this graph contains a Hamiltonian circuit.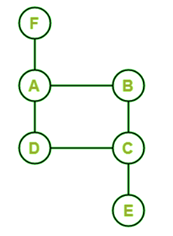

Solution:

The above graph contains the Hamiltonian circuit if there is a path that starts and ends at the same vertex. So we will start from the F, then we can go A, B, C, E. This path does not cover all the vertices (A, B, C, D, E, and F). That's why we can say that this graph does not contain a Hamiltonian circuit.

Important Points

• If we remove one of the edges of Hamiltonian path, then it will be converted into any Hamiltonian circuit.
• If any graph has a Hamiltonian circuit, then it will also have the Hamiltonian path. But the vice versa in this case will not be possible.
• A graph can contain more than one Hamiltonian path and Hamiltonian circuit.

Examples of Hamiltonian Graph:

There are a lot of examples of the Hamiltonian graphs, which are described as follows:

Example 1: In the following graph, we have 6 nodes. Now we have to determine whether this graph is a Hamiltonian graph.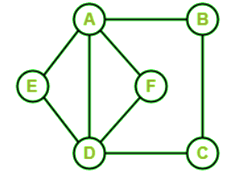

Solution:

This graph does not contain a Hamiltonian path because when we start from A, then we can go to vertices B, C, D, and E, but in this path, vertex F is not covered. This graph does not contain the Hamiltonian circuit also because when we start from A, we can go to vertices B, C, D, E, and A. This can make a circuit, but vertex F is also not covered in this path. So we can say that this graph does not contain a Hamiltonian path and Hamiltonian circuit. Hence, this graph is not a Hamiltonian Graph.

Example 2: In the following graph, we have 5 nodes. Now we have to determine whether this graph is a Hamiltonian graph.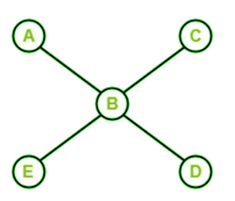

Solution:

This graph does not contain a Hamiltonian path because when we start from A and B, then we can go to one of the three places C, D, and E. So this path does not cover all the vertices. This graph does not contain the Hamiltonian circuit also because any path cannot cover all the vertices and make a circuit. So we can say that this graph is not a Hamiltonian path and a Hamiltonian circuit. Hence, this graph is not a Hamiltonian Graph.

Example 3: In the following graph, we have 7 nodes. Now we have to determine whether this graph is a Hamiltonian graph.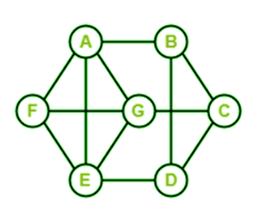

Solution:

This graph contains a Hamiltonian path because when we start from A, then we can go to vertices B, C, D, E, F, and G. This graph also contains the Hamiltonian circuit because when we start from A, then we can go to vertices B, C, D, E, F, G, and A. So we can say that this graph contains a Hamiltonian path and Hamiltonian circuit. The Hamiltonian path and Hamiltonian circuit are described as follows:

ABCDEFG is the Hamiltonian Path of the above graph.

ABCDEFGA is the Hamiltonian circuit of the above graph.

Hence, this graph is a Hamiltonian Graph.

Example 4: In the following graph, we have 9 nodes. Now we have to determine whether this graph is a Hamiltonian graph.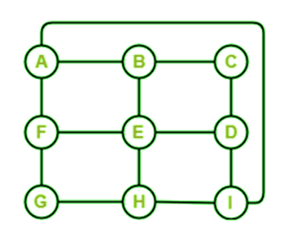

Solution:

This graph contains a Hamiltonian path because when we start from A, then we can go to vertices B, C, D, E, F, G, H, and I. This graph also contains the Hamiltonian circuit because when we start from A, then we can go to vertices B, C, D, E, F, G, H, I, and A. So we can say that this graph contains a Hamiltonian path and Hamiltonian circuit. The Hamiltonian path and Hamiltonian circuit are described as follows:

ABCDEFGHI is the Hamiltonian Path of the above graph.

ABCDEFGHIA is the Hamiltonian circuit of the above graph.

Hence, this graph is a Hamiltonian Graph.

Example 5: In the following graph, we have 5 nodes. Now we have to determine whether this graph is a Hamiltonian graph.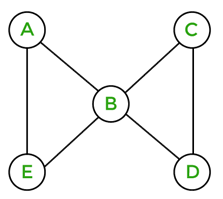

Solution:

This graph does not contain a Hamiltonian path because when we start from A, then we can go to vertices B, C, and D, but in this path, vertex E is not covered. Because of the same reason, this graph also does not contain the Hamiltonian circuit. So we can say that this graph is not a Hamiltonian path and a Hamiltonian circuit. Hence, this graph is not a Hamiltonian Graph.

Example 6: In the following graph, we have 5 nodes. Now we have to determine whether this graph is a Hamiltonian graph.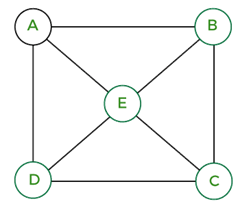

Solution:

This graph contains a Hamiltonian path because when we start from A, then we can go to vertices B, C, D, and E. This graph also contains the Hamiltonian circuit because when we start from A, then we can go to vertices B, C, D, E, and A. So we can say that this graph contains a Hamiltonian path and Hamiltonian circuit. The Hamiltonian path and Hamiltonian circuit are described as follows:

ABCDE is the Hamiltonian Path of the above graph.

ABCDEA is the Hamiltonian circuit of the above graph.

Hence, this graph is a Hamiltonian Graph.