Closure Properties of Relations

Consider a given set A, and the collection of all relations on A. Let P be a property of such relations, such as being symmetric or being transitive. A relation with property P will be called a P-relation. The P-closure of an arbitrary relation R on A, indicated P (R), is a P-relation such that

(1) Reflexive and Symmetric Closures: The next theorem tells us how to obtain the reflexive and symmetric closures of a relation easily.

Theorem: Let R be a relation on a set A. Then:

• R ∪ ∆_A is the reflexive closure of R
• R ∪ R^-1 is the symmetric closure of R.

Example1:

Find the reflexive closure of R.

Solution: R ∪ ∆ is the smallest relation having reflexive property, Hence,

RF = R ∪ ∆ = {(k, k), (k, l), (l, l), (l, m), (m, m), (m, k)}.

Example2: Consider the relation R on A = {4, 5, 6, 7} defined by

Find the symmetric closure of R.

Solution: The smallest relation containing R having the symmetric property is R ∪ R^-1,i.e.

RS = R ∪ R-1 = {(4, 5), (5, 4), (5, 5), (5, 6), (6, 5), (6, 7), (7, 6), (7, 4), (4, 7), (7, 7)}.

(2)Transitive Closures: Consider a relation R on a set A. The transitive closure R of a relation R of a relation R is the smallest transitive relation containing R.

Recall that R² = R◦ R and Rⁿ = R^n-1 ◦ R. We define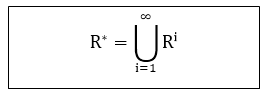

The following Theorem applies:

Theorem1: R^* is the transitive closure of R

Suppose A is a finite set with n elements.

R* = R ∪R2  ∪.....∪ Rn

Theorem 2: Let R be a relation on a set A with n elements. Then

Transitive (R) = R ∪ R2∪.....∪ Rn

Example1: Consider the relation R = {(1, 2), (2, 3), (3, 3)} on A = {1, 2, 3}. Then
R² = R◦ R = {(1, 3), (2, 3), (3, 3)} and R³ = R² ◦ R = {(1, 3), (2, 3), (3, 3)} Accordingly,
Transitive (R) = {(1, 2), (2, 3), (3, 3), (1, 3)}

Example2: Let A = {4, 6, 8, 10} and R = {(4, 4), (4, 10), (6, 6), (6, 8), (8, 10)} is a relation on set A. Determine transitive closure of R.

Solution: The matrix of relation R is shown in fig: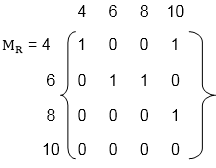

Now, find the powers of M_R as in fig: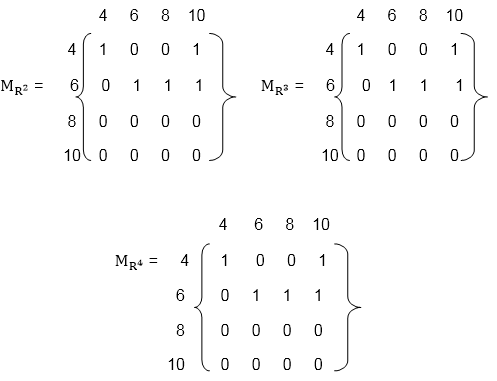

Hence, the transitive closure of M_R is M_R^* as shown in Fig (where M_R^* is the ORing of a power of M_R).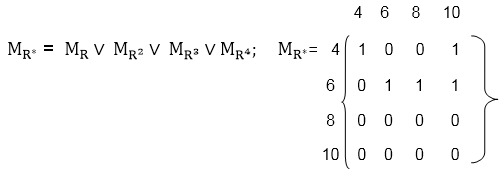

Thus, R^* = {(4, 4), (4, 10), (6, 8), (6, 6), (6, 10), (8, 10)}.

Note: While ORing the power of the matrix R, we can eliminate M_Rⁿ because it is equal to M_R^* if n is even and is equal to M_R³ if n is odd.