Surjective Function in Discrete Mathematics

The surjective function is also known as onto function. With the help of surjective function, we show the mapping of two sets. In this mapping, we will have two sets, f and g. One set is known as the range, and the other set is known as the domain. A function will be known as a surjective function if that function maps every element of x with every element of y.

In other words, we can say that there is an x for every y in such a way that f(x) = y. In case of determining the inverse function, the surjective function plays a very important role. To determine whether the given function is surjective, we have to know about both sets. We can decompose any function into a one-to-one function and an onto function. Now we will learn the definition, properties, and examples of the surjective function.

Definition of Surjective function

A surjective function is a type of function in which its image and codomain are similar to each other. In a surjective function, the range and codomain are also equal to each other. In the surjective function, not even a single element is left out. This is because all the elements of Y are mapped with some element of A. When we have a case where every y codomain has a minimum of one pre-image x domain, then the function will be known as the surjective function. To understand this concept, we will consider an example, which is described as follows:

Suppose X = {x1, x2, x3, x4}, and Y = {1, 2, 3}, then f: X → Y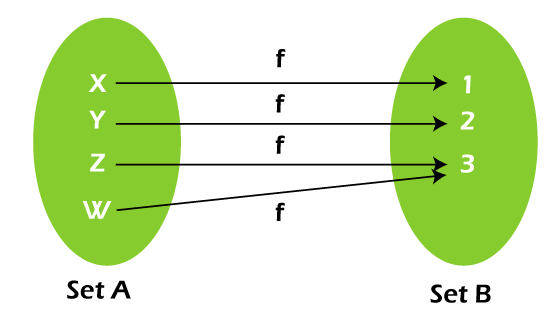

In the above diagram, we can see that we have Set A and Set B. Each and every element of set B has a connection with minimum of one element of set A. In this image, element X of set A is connected or mapped with element 1 of set B. Similarly, Y is connected with 2 and elements Z, and W is connected with the same element, 3. Thus, we can say that the above function is a surjective function or onto function.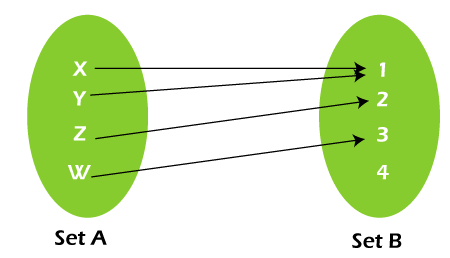

In the above diagram, we can see that we have Set A and Set B. In set B, there is one element that is not mapped with any element of set A. The other elements are similarly mapped, just like the previous elements. That means element X of set A is connected with element 1 of set B. Y is connected with 2, and Z, W are both connected with element 3. Thus, we can say that this function is not a surjective function or onto function.

Example

Suppose there is a surjective function y = f(x), which is used to map all the elements of y to any element of x. Here we will show some examples of surjective functions, which are described as follows:

• For any set X, the identity function will be an onto function.
• Suppose we have a function f: Z → {0, 1, 2}, which is defined by f(n) = n mod 3. This function is a surjective function.

Now we will use a real-life example to more understand this concept.

Suppose there is a function that is used to show the employee id of all the 15 employees of a company. Here domain of a function is indicated by the15 employees, and a codomain of the function is constituted by their employee id. Since, there would be only one employee for every employee id in the system. Thus, this is a real-life example of a surjective function.

Formula for Surjective function

Suppose there is a function from A to B. For this function to be surjective, we have to make sure that we have used all the elements of B. We can determine the number of surjective functions from one set to another set with the help of a formula.

Formula for Number of Surjective function

Suppose there are two sets, A and B. If set A is used to contain m elements and set B is used to contain the n elements, then the total number of surjective functions will be calculated with the help of following formula: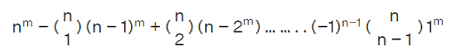

In this formula, if m ≥ n only, then the above formula will be worked. The number of surjective functions will be 0 if m < n. This is because it is impossible for us to use all the elements of B. Therefore,

1. When n < m, in this case, the number of surjective functions = 0.
2. When n = m, in this case, the number of surjective functions = m!.

Calculating Number of Onto functions

Here we will use an example to learn about how we can determine the number of onto functions. Suppose there are two sets, A and B. Set A contains m elements, and B contains 2 elements. In this case, the number of onto or surjective functions is described as follows:

2^m - 2

The above expression can be expressed in the following ways:

• The total number of functions from set A of m elements to the set B of 2 elements is 2^m.
• From the above two functions, the 2 functions will not be surjective if there is a case when all elements are connected with the 1^st element of B or every element is connected with the 2^nd element of B.
• Thus, 2^m - 2 is the total number of surjective functions.

Properties of Surjective function

If the co-domain and the range of a function are similar to each other, then the function will be known as a surjective function or onto function. There are a lot of properties of the surjective function. Some of them are described as follows:

• Each and every element of the surjective function in the codomain must be assigned a minimum one value in the domain.
• There will be a right inverse for every function that is surjective. In other words, we can say that every function that contains a right inverse will be considered a surjective function.
• If the range and co-domain of a function f are equal to each other, then this function f: A → B will be onto function.
• Suppose f: A → B is an arbitrary function. In this case, each and every member of A has an image under f as well as all the image is known as the members of T. The range of this function f will be indicated by set R of these images.

Graph of Surjective function

With the help of a graph, we can very easily find out whether the given function is surjective. To do this, we will compare the range with codomain. The function will be surjective if range and codomain are equal to each other. In a graph, if every horizontal line intersects one or more than one point, then that function will be considered as onto. In the range of any function, if an element is unable to insert the graph of that function or fails the test of horizontal line, in this case, that function will not be a surjective function. For a surjective function, the example of a graph is described by the following image: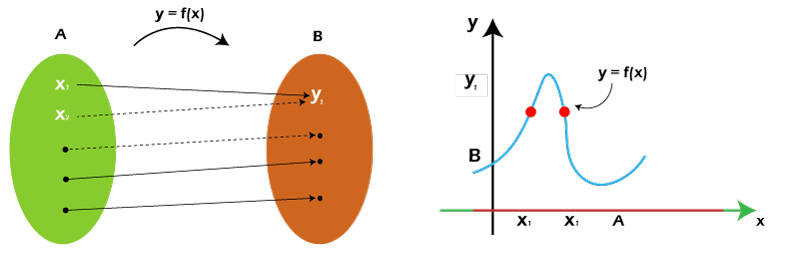

Relationship between Surjective function and Injective function

The surjective and injective both also have one more name. The surjective function is also known as the onto function, and the injective function is also known as the one-to-one function. The main difference between both is that in the injective function, each x can be mapped to only one y, whereas, in the surjective function, all the output values are mapped.

Same as surjective function, the injective function is also an essential prerequisite to learning the inverse function. If there is a function that is both injective and surjective, then that type of function is known as the bijective function. In this function, each and every output set has a connection with the input set, and each and every output value has a connection with only one input value.

In the above diagram, there is a one-to-one or injective because each element on the left set has a connection with only one element on the right set. This is also surjective or onto because each element on the right set has a connection with the left set. Thus it is also bijective because it contains both injective and surjective. For example, function y = x is bijective because it contains both injective and surjective. The bijective functions are known as the special classes of functions because it also contains an inverse.

Examples of Surjective function

There are various examples of surjective functions, which are described as follows:

Example 1: In this example, we will assume X = {4, 5, 7, 8}, and Y = {1, 3}, and f = {(4, 1), (5, 3), (7, 1), (8, 3)}. Now we have to show whether f is an surjective function from X to Y.

Solution: From the above question, we get the following details:

X = {4, 5, 7, 8}

Y = {1, 3}

& f = {(4, 1), (5, 3), (7, 1), (8, 3)}

So, all the elements of set Y contain a domain element on set X. That means the elements 4, 7 of set X, have image 1, and both elements 5, 8 have image 3. Here {1, 3} is known as the range of the function, and that range is equal to Y. Thus, f: X → Y is onto or surjective function.

Example 2: In this example, we have two sets, X and Y where X = {1, 2, 3, 4}, and Y = {x, y, z}. Now we have to determine the number of onto functions.

Solution: By the above question, we get the following details:

X = {1, 2, 3, 4}

Y = {x, y, z}

In this case, n = 4, and m = 3.

Now, we will put the value of n and m in the following formula, and after that, we will get the following:

= 3⁴ - ³C₁(2)⁴ + ³C₂(1)⁴

= 81 - 3 (16) + 3(1)

= 81 - 48 + 3

= 84-48

= 36

Thus, the number of surjective functions from X to Y is 36.

Example 3: In this example, we have a function g: R → R, which is defined as g(x) = 1 + x². Now have to determine whether this function is surjective or onto function.

Solution: Here we have g(x) = 1 + x²

As we know that x² > 0 for all the real numbers. Hence, 1 + x² > 1 or g(x) > 1, and we can also say that range of this function is (1, ∞). The real numbers (R) are also contained by the second set. So this range and codomain are not equal to each other. Hence, the given function is not a surjective function.

Example 4: In this example, we have a function g: R → R, which is defined as g(x) = x². Now have to determine whether this function is surjective or onto function.

Solution: For x we don't have real number because x² = -1. Hence, we can say that the function g(x) = x² is not a surjective function. However, the function g: R → R ≥ 0 defined by g(x) = x². This function is a surjective function with some restricted codomain. So, there is a minimum of one x in real domain X for every y in nonnegative real codomain Y in such a way that x² = y

Important Notes:

When we learn about surjective function or onto function, then there are some points that we should keep in our mind, which are described as follows:

• If the range and codomain are equal, then that function is known as the surjective function.
• We can decompose any function into a one-to-one function and an onto function.