Hashing Function in Discrete mathematicsTo understand the hashing function, we will first learn about the hashing and hash table. HashingHashing is also known as the Message Digest function or Hashing algorithm. In the process of hashing, we are able to convert the large data items into a smaller table. We will use a hash function to map the data. A range of key values can be converted into a range of indexes of an array with the help of hashing. When we compare the hashing with the binary or linear search, the hashing provides us the next-level searching method. Hashing also provides us the facility to update and retrieve any data entry, but the data must be entered into a constant time O(1). The constant time O(1) is used to tell that the operation does not depend on the data's size. A database is contained by the hashing so that it can enable items to be retrieved faster. In the case of digital signature, it can also be used to encrypt or decrypt the data. Hashing is basically a many-to-one mapping that occurs between a larger set and a smaller set. The hash function can be used in a database, memory maps, or dictionaries. Hash Function:A hash function can be described as a fixed process of converting a key into a hash key. The hash function takes a key and maps that key to a value of a certain length. This type of length is known as the Hash value or Hash. The original string of characters is represented with the help of hash value, but these characters are smaller than the original ones. It is also used to transfer the digital signature. It basically sends the hash value and signature to the receiver. The same hash function is used by the receiver to generate the hash value. After that, this generated hash value and the received hash value will be compared. If both the hash values are the same, in this case, the message will be transferred without any type of error. In discrete mathematics, the hash function can be described as a function that is applied to a key. That key is used to generate an integer, and we can use this integer as an address in the hash table. In other words, the hash function 'h' is used to assign memory location 'h(k)' to the record that has contains a key 'k'. In discrete mathematics, all memory locations are possible. This is because the hashing function is onto. A simple hashing function can be defined as follows: Here m is used to indicate the number of memory locations. Hash Table:The hash table can be described as a data structure, which is used to store the key-value pairs. The hash table is used to store the collection of keys or items so that we can easily search any items later. It basically computes an index into an array of slots or buckets with the help of a hash function. From the array of a bucket, we can easily find the desired value. It basically contains an array of the list where each list is called a bucket. It is used to contain the value on the basis of the key. This table is synchronized, and there can be only unique elements in the list. The hash table is described as follows: 
In the above diagram, we can see a hash table with the size of n = 10. In this table, each position is known as the slot. In the above table, there is total of n locations named: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. We can also be called it slot 0, slot 1, slot 2, slot 3, and so on. These slots or locations are used to store some keys. In this table, all the locations/address/slots are empty. As we have learned above that the mapping between a key and the location where key belongs to a hash table is known as the hash function. The hash function chose any key from the collection and placed it into the range of slot names between 0 to n-1. Suppose there are total locations/slots named: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. We will assign these keys 70, 31, 93, 54, 26, and 18 to the slots in the following manner:
The hash table of these data is described as follows: 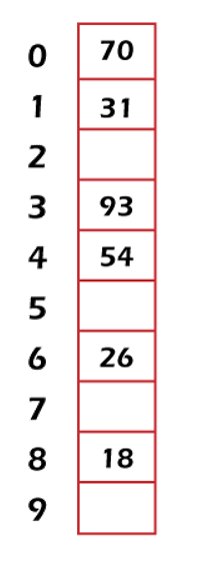
So we can use the hash function to easily search for an item. To do this, the hash function computes the location or slot name for the key. After that, it will check the hash table and find out whether the required key is present on the table or not. On the hash table, two keys do not exist in the same location or slot. Examples of Hash function:Example 1: In this example, we will assume h(k) = k mod 111. The record of the customers will be assigned by the hash function with the social security numbers as keys to memory locations. It will be done in the following way: We can see that location 14 is already occupied. That's why the record will be assigned to the next available location, i.e., 15. The hash table of these records is described as follows: 
Example 2: In this example, we will use the zodiac sign of Chinese such as rabbit, ox, tiger, rabbit, and many more so that we can sort the student submitted midterm into the 12 boxes. Solution: First, we will label a box on the basis of the zodiac sign. So, rat = 0, ox = 1, tiger = 2, rabbit = 3, and so on. After that, we will provide the box number (b) so that it can hold the midterm for a student who is born in year (y). So with the help of following formula, the midterm will be calculated like this: For example, midterm of a student who is born in the year 2000 will be placed at the below box like this: Therefore, it will be a box for the year of dragon. The hashing function is used to contain many more possible keys compared to the memory location because it is not one-to-one. Collision:There is also a case of collision, which will occur when two or more than two records are assigned to the same location. The problem of collision can be resolved with the help of assigning the record to the first free location. The linear probing function can be used to resolve the collision. We can also handle the collisions by using various other methods. The formula related to linear collision resolution is described as follows: In this formula, i runs from 0 to m-1. Example: In this example, we will have array of integer 11. Solution: As we know that h(k) = k mod m here m = 11 So First, the hash table will contain only the address or slot like this: 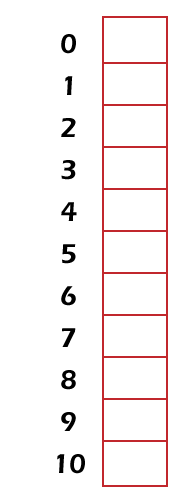
Now we will assign the keys to these addresses like this: 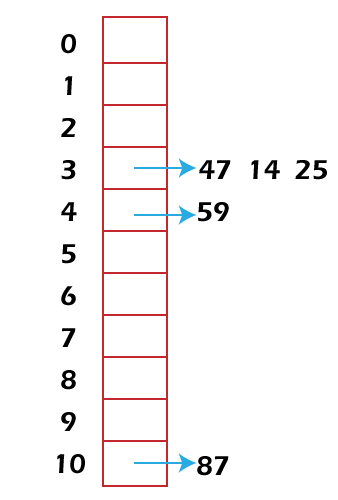
Here we can see that 47, 14, and 25 assign the same memory location 3. In this case, the problem of collision will occur because more than one record/key is assigned to the same location. To solve this problem, we will assign them some other location. First, 47 will be assigned at memory location 3, 14 will be assigned to the next free location, which is 4. 25 will be assigned to the again next free location except 3 and 4, which is 5. So lastly, 47 get location 3, 14 get location 4, and 25 get location 5. The hash table for these new memory locations is described as follows: 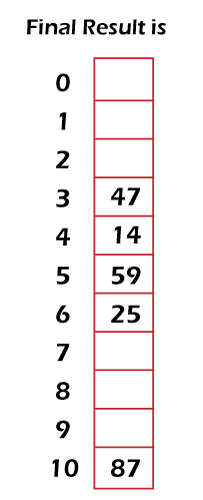
Next TopicDoolittle Algorithm: LU Decomposition
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










