Relationship between number of nodes and height of binary tree

In this section, we are going to learn a lot of cases for the relationship between height of a binary tree and the number of nodes. We should learn about the binary tree and its properties to understand this concept. We will also learn about the minimum and maximum number of nodes.

Binary tree:

A binary tree can be described as a collection of nodes and vertices. It contains a root node, which is the topmost node in the tree. In a tree, we can define the levels of nodes. The root node will always be in Level 0. All the nodes in the binary tree are able to contain maximum 2 children. If the root node has the children, then they will be in level 1.

For example: In this example, we are going to build a binary tree of level 2 with the help of 5 nodes.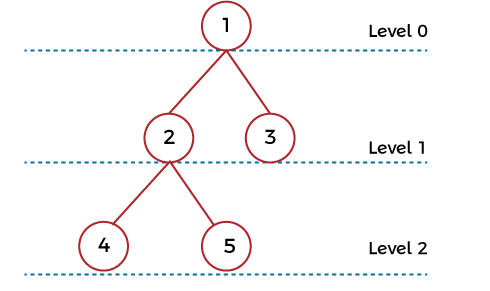

In the above tree, there is a total of 5 nodes, and the root node has a level 0. The children of root node have level 1.

Minimum and maximum number of nodes

The minimum and maximum numbers of nodes are described as follows:

Minimum number of nodes:

We have seen that we require a minimum of 1 node so that we can construct a binary tree with level n. We can calculate the minimum number of nodes with level n in a binary tree with the help of formula: n - 1. The behavior of linked list data structure and the binary tree is the same.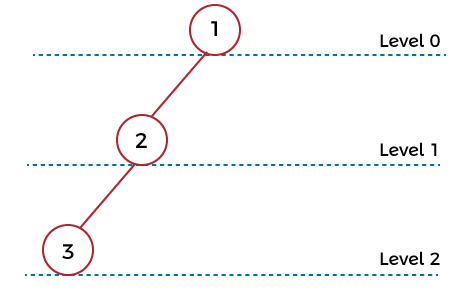

Theorem: The following theorem can be used to find the minimum number of nodes:

Suppose there is a binary tree T with level n where n >= 0. In this case, T will contain at least n + 1 node.

Maximum number of nodes

To construct the maximum number of nodes in a binary tree with level n, we have to make sure that all the internal nodes of this tree will have two children. All the leaf nodes of this tree must be at level n.

For example: In this example, we have a root node at level 0. We have two nodes at level 1, and those nodes are the children of root node. Similarly, we can see that we have 4 nodes at level 2, and these nodes are the children of the nodes at level 1.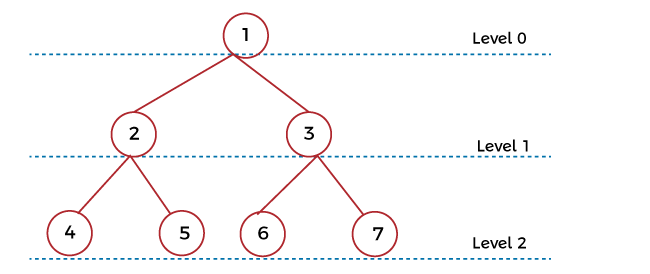

To see the above example, we can say that the number of nodes becomes double from its previous level to the next level. This is the reason every internal node contains two children. The following formula is used to determine the maximum number of nodes of level n:

This type of binary tree is known as the full binary tree.

Theorem: The following theorem can be used to find the maximum number of nodes:

Suppose there is a binary tree T with level n where n >= 0. In this case, T will have at most 2ⁿ⁺¹ -1 nodes.

Calculating max and min height from number of nodes:

The height of a binary search tree can be described as the longest path, which starts from root node to any leaf in a tree. Suppose there is a binary tree that contains n levels. So in this binary tree, the maximum height will be "n-1", and the minimum height will be "floor (log2n)". Now we have two images to understand the height of a binary tree, which is described as follows: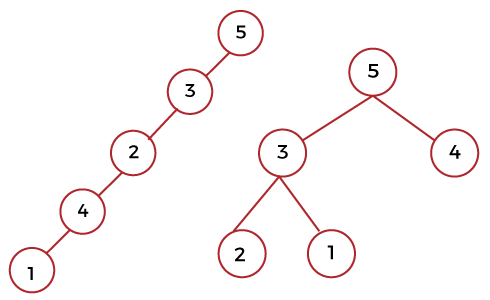

On the right side of above binary tree, there are 5 nodes that contain height floor (log 25) = 2. In this image, the longest path from root node 5 to node 2 is n - 1. Here the right side of image contains 3 levels (level 0, level 1, and level 2). That means total 3 levels. So n = 3, and minimum height will be 3 - 1 = 2. That's why we can say that the height of a binary tree in the right image is 2. On the left side of image, the longest path from the root node to node 1 is n - 1. On the left side, there are total 5 levels. So, n = 5, and minimum height will be 5 - 1 = 4. That's why the height of a binary tree in the left image is 4.

Calculating min and max number of nodes from height:

Suppose there is a binary tree that contains h number of height. So in this binary tree, the minimum number of nodes will be h + 1 (in the case of right-skewed and left-skewed binary trees).

For example: In the below image, left side of a binary tree shows height 2, which contains 3 nodes.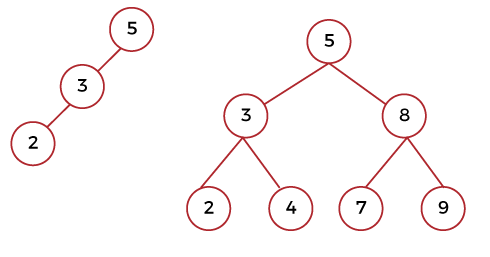

Suppose there is a binary tree that contains height h. If all the levels of a tree are completely full, in this case, the total number of nodes will be determined by the following formula:

For example: In the above image, the right side of binary tree shows height 2, which contains 2 ^ (2 + 1) - 1 = 7 nodes.

Binary search tree:

There are two children in a binary search tree, i.e., left child and right child. The value of left child of a node must be less than the value of parent, and the value of right child of a node must be greater than the value of parent.

Calculating min and max height from the number of nodes:

Suppose there is a binary search tree that contains n number of nodes. So in this binary search tree, the maximum height will be "n-1", and the minimum height will be "ceil (log2n)".

Calculating min and max number of nodes from height:

Suppose there is a binary search tree that contains height h. So in this binary search tree, the minimum number of nodes will be h + 1 (in the case of right-skewed and left-skewed binary search trees).

Suppose there is a binary search tree that contains height h. If all the levels of a tree are completely full, in this case, the total number of nodes will be determined by the following formula:

In conclusion, we can say that the rules of a binary tree and binary search tree are the same, and we are also able to visualize them in the same way.