Logical Connectives in Discrete mathematics

If we want to learn the logical connectives, we have to first learn about the propositions. After that, we can understand the logical connectives.

Propositions

The proposition can be described as a declarative statement, which means it is used to declare some facts. Propositional logic can be indicated as either true or false, but we cannot indicate it in both ways. In this section, we are going to learn about the connectivity in propositional logic.

Logical connectivity

Logical connectivity can be described as the operators that are used to connect one or more than one propositions or predicate logic. On the basis of the input logic and connectivity, which is used to connect the propositions, we will get the resultant logic. The propositional logic is used to contain 5 basic connectives, which are described as follows:

1. Negation
2. Conjunction
3. Disjunction
4. Conditional
5. Bi-conditional

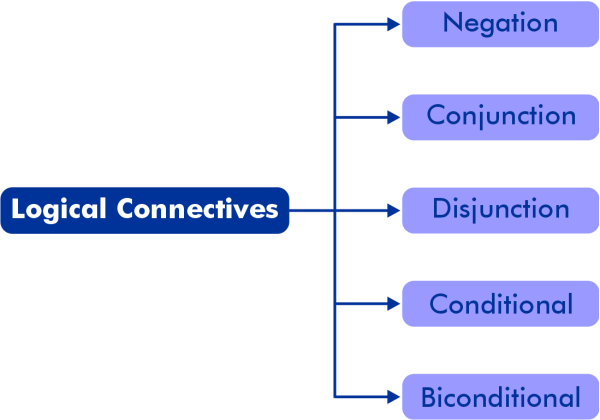
Names of connectives, connective words, and symbols of Propositional logic are described as follows:

Now we will discuss all of these connectives one by one, which is shown below:

Negation

The symbol ∼ is used to indicate the negation. If there is a proposition p, then the negation of p will also be a proposition, which contains the following properties:

• When p is true, then the negation of p will be false.
• When p is false, then the negation of p will be true.

Truth table:

The truth table of negation is shown below:

Example:

The example to show the negation is described as follows:

Conjunction

The conjunction is indicated by the symbol ∧. If there are two propositions, p and q, then the conjunction of p and q will also be a proposition, which contains the following properties:

• When p and q are true, then the conjunction of them will be true.
• When p and q are false, then the conjunction of them will be false.

Truth table:

The truth table of conjunction is shown below:

Example:

The example to show the conjunction is described as follows:

Disjunction:

Disjunction is indicated by the symbol ∨. If there are two propositions, p and q, then the disjunction of p and q will also be a proposition, which contains the following properties:

• When p and q are false, then the disjunction of them will be false.
• When either p or q or both are true, then the disjunction of them will be true.

Truth table:

The truth table of disjunction is shown below:

Example:

The example to show the disjunction is described as follows:

Conditional:

The conditional propositional is also known as the implication proposition. It is indicated by the symbol →. If there are two propositions, p and q, then the conditional of p and q will also be a proposition, which contains the following properties:

• If there is a proposition that has the form "if p then q", then that type of proposition will be known as the implication or conditional proposition.
• When p is false, or p and q are true, then the implication of them will be true.
• When p is true, and q is false, then the implication of them will be false.

Truth table:

The truth table of implication is shown below:

Example:

The example to show the implication proposition is described as follows:

Bi-conditional:

The bi-conditional propositional is also known as the bi-implication proposition. It is indicated by the symbol ↔. If there are two propositions, p and q, then the bi-conditional of p and q will also be a proposition, which contains the following properties:

• If there is a proposition that has the form "p if and only if q", then that type of proposition will be known as a bi-implication or bi-conditional proposition.
• When both p and q are true, or p and q both are false, then the bi-implication of them will be true.
• In all the other cases, then the bi-conditional of them will be false.

Truth table:

The truth table of bi-implication is shown below:

Example:

The example to show the bi-implication proposition is described as follows:

Important Notes:

There are some important notes related to logical connectives, which are described as follows:

Note 1:

• Negation: It is equal to the NOT gate of digital electronics.
• Conjunction: It is equal to the AND gate of digital electronics.
• Disjunction: It is equal to the OR gate of digital electronics.
• Bi-conditional: It is equal to the EX-NOR gate of digital electronics.

Note 2:

• Some priority must be contained by each logical connective.
• At the time of solving the questions, the order of this priority will be important.
• The decreasing order of priority is shown in the following image:

Note 3:

• The commutative and associative properties are contained by the negation, disjunction, conjunction, and bi-implication or bi-conditional.
• Commutative or associative properties do not contain by implication or conditional.