Algorithms and Functions

Algorithm: An algorithm is a step-by-step method for solving some problem.

Characteristics of Algorithms:

Algorithms generally have the following characteristics:

1. Input: The algorithm receives input. Zero or more quantities are externally supplied.
2. Output: The algorithm produces output. At least one quantity is produced.
3. Precision: The steps are precisely stated. Each instruction is clear and unambiguous.
4. Feasibility: It must be feasible to execute each instruction.
5. Flexibility: It should also be possible to make changes in the algorithm without putting so much effort on it.
6. Generality: The algorithm applies to a set of inputs.
7. Finiteness: Algorithm must complete after a finite number of instruction have been executed.

Analysis (Complexity) of Algorithms

The Analysis of an algorithm refers to the process of deriving estimates for the time and space needed to execute the algorithm.

It is important to estimate the time (e.g., the number of steps) and space (e.g., the number of variables) required by algorithms. Knowing the time and space required by algorithm allows us to compare the algorithms that solve the same problem. For example, if one algorithm takes n steps to solve a problem and another algorithm takes n^2 steps to solve the same problem, we would prefer the first algorithm. This estimation of time and space needed to execute the algorithm is called the time and space complexity of the algorithm.

      The time required to execute an algorithm is a function of the input. Instead of dealing directly with the input, parameters are used to characterize the size of the input. e.g. if the input is a set containing n elements, the size of the input n. There are three cases worth noting about the time complexity of an algorithm since determining the exact time complexity of an algorithm in a difficult task.

• Worst-case: f (n) represent by the maximum number of steps taken on any instance of size n.
• Best-case: f (n) represent by the minimum number of steps taken on any instance of size n.
• Average case: f (n) represent by the average number of steps taken on any instance of size n.

Asymptotic Notations

Asymptotic Notations are used to describe the execution time of an algorithm. The notations show the order of growth of functions. Here the time taken by an algorithm is mapped regarding mathematical functions. There are many asymptotic notations like 0, θ, Ω,w each having its importance.

1. Big-oh notation: The function f (n) =O (g (n)) [read as "f of n is big-oh of g of n"] if and only if exist positive constant c and n₀ such that

f (n) ⩽ C x g (n) for all n, n ≥ n0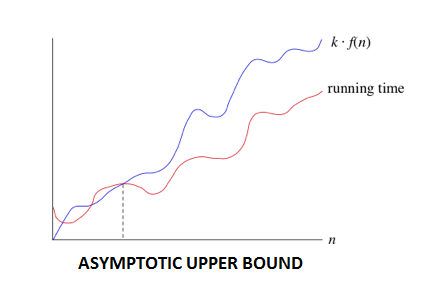

Example1: The function 4n + 3 = O (n) as 4n + 3 ⩽ 5n for all n ≥.

Example2: The function 20n² + 5n + 2 = O (n²) as 20n²+ 5n +2⩽21n² for all n ≥.

2. Omega (Ω) Notation: The function f (n) = Ω (g (n)) [read as "f of n is omega of g of n"] if and only if there exists positive constant c and n₀ such that

f (n) ≥ C* g (n) for all n, n ≥ n0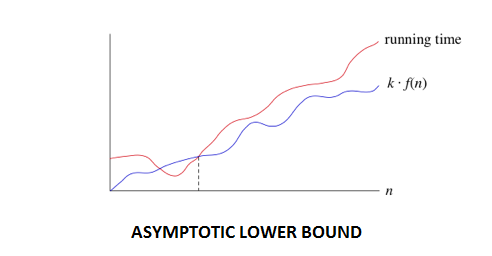

Example1: The function 4n + 3 = Ω (n) as 4n + 3 ≥ 4n for all n ≥1.

Example2: The function 20n²+ 5n +2 = Ω (n) as 20n²+ 5n +2 ≥ 20n² for all n ≥1.

3. Theta (θ): The function f (n) = θ (g (n)) [read as "f is the theta of g of n"] if and only if there exists positive constant k₁, k₂ and k₀ such that

k1* g (n) ≤ f (n)≤k2* g(n)for all n, n≥n0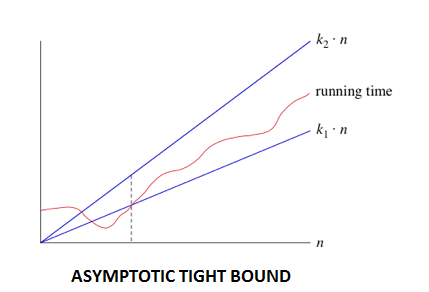

Example1: The function 4n + 3 = θ (n) as 4n + 3 ≥ 4n for all n ≥ 3 and 4n + 3 ≤ 5n for all n ≥ 3.

Example2: The function 20n²+ 5n +2 = θ (n²) as 20n²+ 5n +2 ≤ 21n² for all n ≥1 and 20n²+ 5n +2 ≥ 20n² for all n ≥ 1.