Independent events in Probability

Independent events are events that do not depend on the occurrence of each other. It means that the happening or failure of one event does not affect the happening or failure of the other event.

For example,

Tossing a dice

There are six numbers mentioned on a dice with 6 faces. A single throw of dice can result in the occurrence of any number from the numbers 1, 2, 3, 4, 5, and 6. We can get any outcome on every single throw.

Let's consider the two outcomes. In the first outcome, we get the number 2, and in the second outcome, we get the number 5. In both cases, the occurrence is independent of each other. It is a type of independent event in Probability.

What are dependent events?

If an event is affected by the occurrence of the other event, it is known as dependent event. If the event A and event B are dependent events, i.e., the occurrence of A depends on the occurrence of B, then the probability P (AB) is given by:

P (AB) or P(A∩B) = P (A) P(B/A)

Where,

P(B/A) is the conditional probability of B given A has occurred.

P (AB) or P(A∩B) is the probability of both the events A and B happening as a result of two trials.

Independent events formula

If the event A and event B are independent events, i.e., the occurrence of A does not depend on the occurrence of B, then the probability P (AB) is given by:

P (AB) or P(A∩B) = P (A) P(B)

Where,

P(B/A) = P(B)

It is because A and B are the two independent events.

The probability that the event happens = P

The probability that the event fails = (1 - P)

Let P₁ and P₂ be the probability of the two independent events

The probability that both the events happens = P₁ P₂

The probability that both the events fails = (1 - P₁) (1 - P₂)

The probability that the first event happens and the second event fails = P₁(1 - P₂)

The probability that the first event fails and the second event happens = (1 - P₁) P₂

The probability that at least one event happens

1 - (Probability that both fails)

1 - ((1 - P₁) (1 - P₂))

It is also termed as the cumulative probability

Similarly, for the n number of independent events, the probability that at least one event happens is:

1 - ((1 - P₁) (1 - P₂) (1 - P₃) (1 - P₄)… (1 - P_n))

Venn diagram

The Venn diagram of two events A and B is shown below: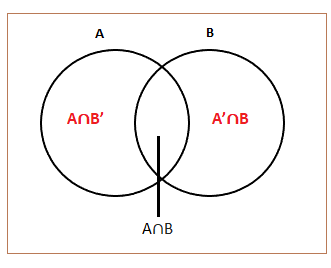

If events A and B are independent,

P(A∩B) = P(A) x P(B)

A∩B is the common area between the two regions A and B.

A is the area of region A, including the common region

B is the area of region A, including the common region

A∪B is the total area of the two regions A and B.

A'∩B is the area of the region A excluding the common region

Hence,

P(A'∩B) = P(A) - P(A∩B)

A∩B' is the area of the region B excluding the common region

Hence,

P(A∩B') = P(B) - P(A∩B)

What are mutually exclusive events?

Mutual events are events that do not occur simultaneously. For example, tossing a coin and throwing dice. In the first case, a Head and a Tail while tossing a coin cannot occur simultaneously. Similarly, numbers 2, 3, 4, or 5 while throwing a dice cannot occur simultaneously. We require a separate outcome for every toss or throw. Independent events can have common outcomes, while mutually exclusive events cannot. There is no common area between any two mutually exclusive events.

Thus,

In the case of independent events,

P(A∩B) = P(A) x P(B)

In the case of mutually exclusive events,

P(A∩B) = 0

Examples

Let's consider some examples based on the independent events in probability.

Example 1: Two cards are drawn in a succession from a pack of 52 cards. Find the chance that first is a queen and the second is a king if the first card is (a) replaced and (b) not replaced.

Solution:

Total number of cards = 52

Total number of queen cards = 4

Total number of king cards = 4

Probability that a queen is drawn from a deck of 52 cards

= 4/52

= 1/13

Probability that a king is drawn from a deck of 52 cards

= 4/52

= 1/13

a) Probability that a first is a queen = 4/52 = 1/13

Since the cards are replaced, the next card will be selected from the 52 cards only.

Probability that a second is a king = 4/52 = 1/13

The probability that first is a queen and the second is a king = (Probability that a first is a queen) (Probability that a second is a king)

= 1/13 x 1/13

= 1/169

b) Probability that a first is a queen = 4/52 = 1/13

Since the cards are not replaced, the next card will be selected from the 51 cards only.

Probability that a second is a king = 4/51

The probability that first is a queen and the second is a king = (Probability that a first is a queen) (Probability that a second is a king)

= 1/13 x 4/51

= 4/663

Example 2: Two cards are drawn in a succession from a pack of 52 cards. Find the chance that first is a diamond and the second is a club card if the first card is replaced.

Solution:

Total number of cards = 52

Total number of diamond cards = 13

Total number of club cards = 13

Probability that a diamond is drawn from a deck of 52 cards

= 13/52

= 1/4

Probability that a club is drawn from a deck of 52 cards

= 13/52

= 1/4

Probability that first is a diamond and the second is a club = (Probability that a first is a diamond) (Probability that a second is a club)

= 1/4 x 1/4

= 1/16

Example 3: Two cards are drawn in a succession from a pack of 52 cards. Find the chance that first is a jack and the second is not a jack if the first card is replaced.

Solution:

Total number of cards = 52

Total number of jack cards = 4

Probability that a jack is drawn from a deck of 52 cards

= 4/52

= 1/13

Probability that the second card is not a jack

= 1 - (probability that a card is jack)

= 1 - 1/4

= 3/4

Probability that first is a jack and the second is not a jack is:

= 1/4 x 3/4

= 3/16

Example 4: A pair of dice is tossed twice. Find the probability of scoring 8 points (a) once (b) at least once (c) twice.

Solution: Total chances of tossing a pair of die twice = 36

The sum of 8 can be obtained as (2, 6), (6, 2), (5, 3), (3, 5), (4, 4)

= 5 ways

Probability of getting 8 point = 5/36

Probability of not getting a sum 8 = (1 - 5/36)

= 31/36

a) There are two cases of getting a score of 8 once. The first case is the chance of getting the 8 on first toss and the second case is the chance of getting the 8 on the second toss.

Probability of scoring 8 points once = (Probability of getting 8 in the first toss) (Probability of not getting 8 in the second toss)

= 5/36 × 31/36

= 155/ 1296

Probability of scoring 8 points once = (Probability of not getting 8 in the first toss) (Probability of getting 8 in the second toss)

= 31/36 × 5/36

= 155/ 1296

Since, both are mutually exclusive events, the addition law of probability applies.

= 155/ 1296 + 155/ 1296

= 310/1296

= 155/648

b) Probability of scoring 8 points at least once = 1 - Probability of scoring 8 points in neither toss

Probability of not getting 8 in either toss = 31/36 × 31/36

= 961/1296

Probability of scoring 8 points at least once = (1 - 961/1296)

= 335/1296

Probability of scoring 8 points at least once = Probability of scoring 8 points once + Probability of scoring 8 points twice

= 310/1296 + 25/1296

= 335/1296

c) Probability of scoring 8 points twice = (Probability of getting 8 in the first toss) (Probability of getting 8 in the second toss)

= 5/36 × 5/36

= 25 / 1296

Example 5: A pair of dice is tossed thrice. Find the probability of scoring 15 points twice.

Solution: Total chances of tossing a pair of die thrice = 216

The sum of 15 can be obtained as (6, 6, 3), (3, 6, 6), (6, 3, 6), (5, 5, 5), (5, 6, 4), (6, 5, 4), (4, 5, 6), (4, 6, 5), (5, 4, 6), (6, 4, 5)

= 10 ways

Probability of getting 15 point = 10/216

Probability of not getting a sum 15 = (1 - 10/216)

= 206/216

Probability of scoring 15 points twice = (Probability of getting 15 in the first toss) (Probability of getting 15 in the second toss)

= 10/216 × 10/216

= 100/46656

= 25/11664

Example 6: Let A and B be two independent events such that P(A) = 0.5 and P(B) = 0.8. Find the P(A or B), P(A and B), P(A not B), P(B not A), and P(neither A nor B).

Solution:

Given: P(A) = 0.5

P (B) = 0.8

To find: P (A∪B), P(A∩B), P(A∩B'), P(B∩A'), and P(A'∩B')

Since, the given two events are independent; we will consider the similar formulas.

P(A∩B) = P(A) x P(B)

P(A∩B) = 0.5 x 0.8

P(A∩B) = 0.4

P (A∪B) = P(A) + P(B) - P(A∩B)

P (A∪B) = 0.5 + 0.8 - 0.4

P (A∪B) = 0.9

P(A∩B') = P(A) - P(A∩B)