Incident coloring in Discrete mathematics

In 1993, Brualdi and Massey discovered the concept of incident coloring. Suppose there is a multi-graph G = (V, E) with the order p and size q, I(G) = {(v, e) | v ∈ V, e ∈ E. Here v is used to indicate the vertex of G, and e is used to indicate the edge of G. Here, edge e is incident with v}. Now there are total 2 incidences (v, e) and (w, f), which will be adjacent if it contains one of the following conditions:

1. v = w
2. e = f
3. vw = e and f

The incidence coloring of G can be described as the process of assigning coloring of its incidence in such a way that the neighboring incidences will be assigned different colors. With the help of symbol Xi(G), the incidence coloring number of G or the incidence chromatic number is indicated, which can be described as the smallest number of colors which is needed in the incidence coloring.

Example of Incidence coloring

In this example, we will use a graph to understand the incidence coloring, which is described as follows: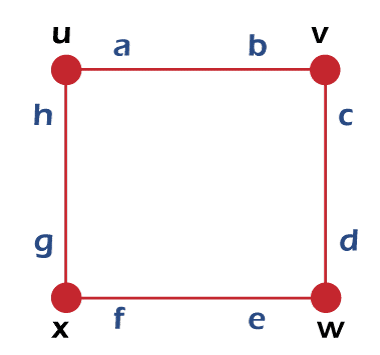

In the above image, we have a set of incidence, which is indicated by {a, b, c, d, ...., h} of cycle C4 on 4 vertices, i.e., {u, v, w, x}. We can see that the incidence 'a' corresponds to the pair (v, uv). On the other hand, incidence 'b' is used to correspond to the pair (v, vu). In the below image, we will see the incidence coloring of C4 with the help of 4 colors.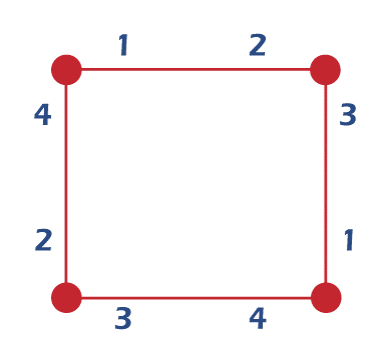

In this image, we have easily checked that with the help of 3 colors, we cannot color the incidences of C4.

Notation:

We should know a lot of notations before learning the concept of incidence coloring. All of these notations are described as follows:

For every graph G, the vertex set is indicated with the help of V(G), the edge set is indicated with the help of E(G), the set of incidences is indicated with the help of I(G), and its maximum degree is indicated with the help of ?(G). The degree of a vertex v is indicated with the help of deg(v). With the help of Xi(G), the incidence chromatic number of G can be indicated. Suppose there is a vertex v in graph G. If there is a set of incidences with the form (u, uv), then it will be indicated with the help of A+(v). If the set of incidence contains the form (v, vu), then it will be indicated with the help of A-(v). Now we will observe that both incidences A+(v) and A-(v) are used to have exactly deg(v) incidences.

(k-p) incidence colorings

Suppose there is an incidence (k, p) coloring of a graph G where k is the number of colors to color the A+(v). If we use at most p number of colors to color the incidence A+(v) for every vertex v in V(G), in this case, an incidence coloring of G with the help of k colors will be known as the incidence (k, p) coloring of graph G. For an incidence (k, p)-coloring of a graph G, the symbol Xi, p(G) is used to indicated the smallest number of required colors. We have observed that the Xi(G) ≤ Xi, p(G) for every p ≥ 1 and for every G.

Links with other notations

We will assume that there is an undirected graph IG(G), which contains the edges and vertices. The vertices of this graph are indicated with the help of incidence of I(G), and the edges of this graph are indicated with the help of those types of pairs of incidences that are adjacent to the graph G. So we can say that the incidence graph of G is equivalent to the graph IG(G). It is concluded that an incidence k coloring of G can also be known as proper vertex k coloring of IG(G).

We will assume that there is a bipartite graph H, which can be defined as V(H) = V(G) ∪ E(G) and E(H) = {(v, e), e ∈ E(G), here e and v are used to show the incidence in G}. The incidence of I(G) can be corresponded by each edge of E(G). The strong edge coloring of H can be corresponded by the incidence coloring of G. (The proper coloring of edge E(H) is used to show that each color class must have an induced matching in the bipartite graph H).

Now we will assume there is an undirected graph denoted by G and also a bigraph denoted by G*. The bigraph G* can be obtained with the help of G. For this, we have to just replace each and every edge of E(G) with two opposite arcs. If there is an incidence (v, e) of I(G), which have e = vw, in this case, it will be associative with the arc vw in A(G*). So, in other words, we can say that an incidence coloring of a graph G will also be viewed as arc coloring of G* if it satisfies the following conditions:

1. If there are two arcs in the form uv and uw that have the same source vertex, then these arcs must assign different colors.
2. If the two consecutive arcs are in the form uv and vw, they must be assigned different colors.

Finally, if we have an undirected graph G which contains f and f is a (k, 1)-incidence coloring, in this case, the set {f(u, uv), u,v ∈ V(G)} will have the cardinality 1 for each and every vertex v in V(G). For every two vertices, u and v, we can very easily see that c(u) ≠ c(v) because the distance between these vertices in G is 1 or 2. For every vertex v, the mapping will be known as 'well defined' if the mapping c is defined by c(v) = f(u, uv).