Addition of Matrices in Discrete mathematicsMatrix addition can be described as a process of addition of two or more than two matrices. A matrix is used to contain the rectangular array of numbers, and all these numbers, expressions, or symbols will be arranged in the form of rows and columns. Unlike arithmetic addition of numbers, there are various different kinds of rules which are followed by matrix addition. There are a lot of ways in which we can perform the addition of matrices, but there are two most commonly used ways for matrix addition, i.e., a direct sum of matrices and element-wise matrix addition. There are various kinds of operations that can be performed on matrices, like subtraction, multiplication, addition, etc. In this section, we will learn only about the operation of matrix addition. What is Matrix AdditionMatrix addition can be described as a process of addition of corresponding elements of two or more than two matrices. If we want to do the addition of matrices, then we will always check size of the matrices or the order of matrices. When we are talking about the same order of the matrices, then we actually mean about the same number of columns and the number of rows. Only after that, we will be able to add corresponding elements of the matrices. If two matrices contain different orders, in this case, we will not be able to do matrix addition. If the number of horizontal rows of the first matrix is m and the number of vertical rows of the second matrix is n, then that type of matrix will be known as the m*n dimension matrix. If the same order is contained by two matrices, A and B, where A = [aij]m*n and B = [bij]m*n, in this case, the addition of these matrices will be described as follows:
A + B = [aij]m*n + [bij]m*n = [aij + bij]m*n
In case of algebraic expression, the addition of expressions will be done by adding the corresponding terms in an expression. Just like the addition of algebraic expressions, the addition of matrices will be performed by adding the corresponding terms in matrix. We can define the addition of a matrix with the help of considering two criteria, which are described as follows:
Definition of Addition of matricesIn case of matrix, there are a lot of operations, but matrix addition is one of the basic operations. With the help of adding corresponding elements of matrices, we will be able to add two or more than two matrices that have the same order. Suppose there are two matrices, A and B, where A = [aij] and B = [bij]. If these matrices contain the same number of dimensions, then it means that these matrices will contain the same number of rows and columns. In the following way, we can indicate the addition of matrices A and B like this:
A + B = [aij] + [bij] = [aij + bij]
Types of Matrix AdditionThere are two types of matrix addition. The first one is "Element wise matrix addition", which is used to add the corresponding elements of two or more than two matrices. The second one is "Direct sum matrix addition", which is used to calculate the direct sum of matrices. Now we will discuss both types of matrices one by one in the following way. Element-wise matrix additionIf there are two matrices and both the matrices contain an equal number of rows and columns, only then it will be possible to do the addition of matrices. At the time of adding two matrices, we are going to add the elements in each row and column of one matrix to the respective elements in rows and columns of the second matrix. Suppose there are two matrices, A and B, which have the same order, m*n. Here m is used to indicate the number of rows, and n is used to indicate the number of columns of two matrices. It can be indicated as A = [aij] and B = [bij]. Now we will use the following way to indicate the addition of A and B, i.e., A+B = [aij] + [bij] = [aij + bij]. Here ij is used to indicate the position of each element in the ith and jth column. The matrix m*n will be the dimension of this sum matrix A+B. 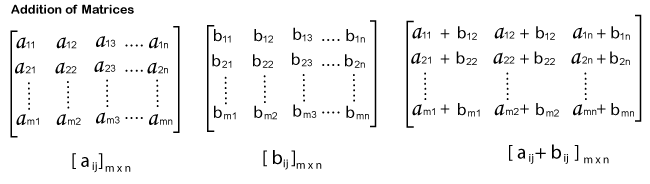
It is a type of operation that is less often used in case of matrices. The symbol ⊕ is used to indicate the direct sum of matrices. The order of matrices must be the same at the time of calculating the direct sum of two matrices. Suppose there are two matrices, X and Y, which is used to have the order m*n and p*q, respectively. Here X is used to contain the m number of rows and n number of columns, and Y is used to contain the p number of rows and q number of columns. 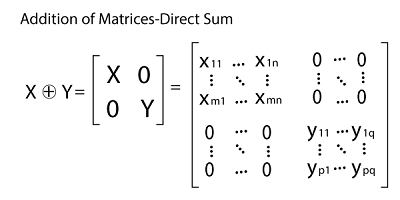
Addition of 2*2 matricesAs we have learned that if there are an equal number of rows and columns in the matrices, only then we will be able to do the addition of those matrices. The most commonly used matrices to perform addition operations will have the order 2*2 and 3*3. If we want to do the addition of matrices which has order 2*2, then we can say that the matrices will have 2 rows and 2 columns. Suppose we have two 2*2 matrices, A and B. The elements of A and B matrices are described as follows: 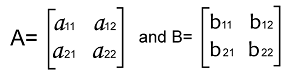
In the following way, we will do the addition of these matrices A and B like this: a11 + b11 a12 + b12 a22 + b22 a21 + b21 The result of this addition can be shown in another way, which is described as follows: 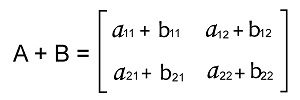
Now we will better understand the concept of matrix addition which has 2*2 dimensions, with the help of using an example of matrices A and B. 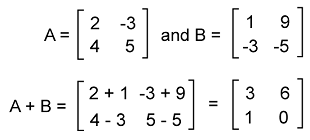
Addition of 3*3 matricesIf there are two 3*3 matrices and we try to add them, then it will imply that the matrices which we are going to add from one another will have the 3 rows and 3 columns. In case of the addition of matrices, the order of these matrices must be the same, and because of the same order, we can add the corresponding elements. Suppose we have two 3*3 matrices, A and B. In the following way, we can represent the elements of the matrices like this: 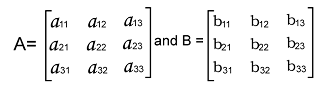
In the following way, we will do the addition of these matrices A and B like this: 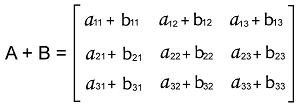
Now we will better understand the concept of matrix addition which has 3*3 dimensions, with the help of using an example of matrices A and B. 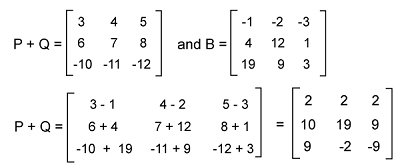
Properties of Addition of matricesThe addition of matrices and the addition of numbers both contain the same properties, i.e., additive identity, associative law, additive inverse, and commutative law, etc. There is an important necessity that must be contained by matrix addition if they want to contain all these properties, i.e., we can define the addition of matrices if matrices contain the same order. Here we will assume that there are three m*n matrices, A, B, and C. Now we will explain all these properties one by one like this: Commutative property:If there are two matrices, A = [aij] and B = [bij], which contain the m*n order, in this case, the addition of matrices A+B will be equal to B+A. That means if we add the two given matrices and add the matrices by changing their position, then it will generate the same result. So the addition of matrices contains the following relation: A+B = B+A Hence the matrix addition is commutative. Associative Property:If there are three matrices, A = [aij], B = [bij], and C = [cij], which contain the m*n order, in this case, the addition of these matrices will be associative, i.e., (A+B) + C = A + (B+C). That means if we add the three given matrices with the help of brackets and add the matrices by changing the position of brackets, then it will generate the same result. That means the addition of matrices will not be affected by how we group the numbers. So the addition of matrices contains the following relation: (A+B) + C = A + (B+C) Hence the matrix addition is associative. Existence of Additive identitySuppose there is a matrix A = [aij] which contains the order m*n. If there is an additive identity of A, and a zero matrix 0, which contains the m*n order, and if we add them, then the resultant matrix will be a zero matrix with the same order, i.e., A + 0 = 0 + A = A. That means if we add a given matrix and a zero matrix, then it will generate the given matrix as the result matrix. Here zero matrix is used to indicate the additive identity for matrix addition. So the addition of matrices contains the following relation: A + 0 = 0 + A = 0 Hence the matrix addition is additive identity. Existence of Additive inverseSuppose there is a matrix A = [aij] which contains the order m*n. The word additive inverse is used to indicate that when we change the sign of a given matrix and add this changed matrix to the original matrix, then we will get 0 as a resultant matrix. If there is a matrix A, then the negation of this matrix will be -A = [-aij], which will also have an order m*n. The existence of addition inverse contains the following relation: A + (-A) = 0 Here (-A) is used to indicate the additive inverse in matrix addition. Hence the matrix addition is additive inverse. Transpose PropertySuppose there are two matrices, A and B. We can get the transpose of addition of these two matrices with the help of doing the addition of transpose of individual matrices in reverse order. The transpose of A and B is described as follows: (A + B)T = AT + BT Here T is used to indicate the transpose. Determinant propertySuppose there are two matrices, A and B. We can get the determinant of addition of these two matrices with the help of doing the addition of determinants of the respective matrices. The determinant of A and B is described as follows: |A + B| = |A| + |B| Important points on Matrix Addition
Examples of Matrix AdditionThere are a lot of examples of matrix addition, and some of them are described as follows: Example 1: In this example, we have two matrices with 1*2 dimensions, A and B. Some elements of these matrices are a11 = 1, a12 = 4 and b11 = -1 and b12 = -8. Now we have to determine the element of sum matrix C = A + B explicitly. Solution: From the question, we know that the given matrices contain the same order 1*2. So we can add matrix A and matrix B. Now we will perform the addition of A and B by adding the corresponding elements of these matrices. We will get the following values by adding the corresponding elements of A and B like this: c11 = a11 + b11 = 1 + (-1) = 0 c12 = a12 + b12 = 4 + (-8) = -4 Hence c11 = 0, and c12 = -4. Example 2: In this example, we have A and B, two matrices. Some elements of A and B are a23 = -17 and b23 = 20, respectively. Now we will use the definition of matrix addition and find out the element of 2nd row and 3rd column of the A+B matrix. Solution: We will find out the element of 2nd row and 3rd column of A+B with the help of calculating the a23+b23 in the following way: a23 + b23 = -17+20 = 3 Hence the element of 2nd row and 3rd column of A+B is 3. Example 3: In this example, we have A and B, two matrices, and we have to determine whether we can add both matrices or not. The elements of A and B are described as follows: 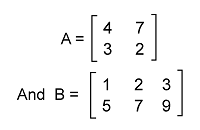
Solution: As we can see that the order of matrix A is 2*2, and the order of matrix B is 3*2. So the order of both matrices is not the same. That's why we cannot add the matrices A and B together. Example 4: In this example, there are two matrices, A and B and we have to find out whether we can add both matrices or not. The elements of A and B are described as follows: 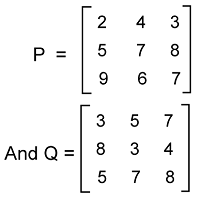
Solution: As we can see that the order of matrix A and matrix B is 3*3. So because of the same order, we can do the addition of these matrices. To do the addition of A and B, we will add the element of P into the corresponding elements of Q. After doing this, the value of matrix A+B will be: 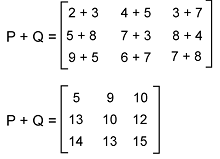
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










