Python Tutorial
Python OOPs
Python MySQL
Python MongoDB
Python SQLite
Python Questions
Plotly
Python Tkinter (GUI)
Python Web Blocker
Python MCQ
Related Tutorials
Python Programs
8 Puzzle problem in PythonThe 8 puzzle problem solution is covered in this article. A 3 by 3 board with 8 tiles (each tile has a number from 1 to 8) and a single empty space is provided. The goal is to use the vacant space to arrange the numbers on the tiles such that they match the final arrangement. Four neighbouring (left, right, above, and below) tiles can be moved into the available area. For instance, 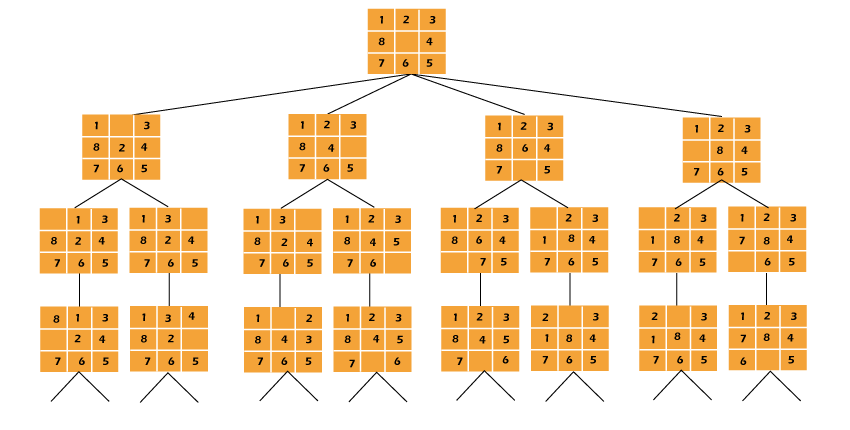
1. DFS (Brute - Force) :On the state-space tree (Set of all configurations of a particular issue, i.e., all states that may be reached from the beginning state), we can do a depth-first search. 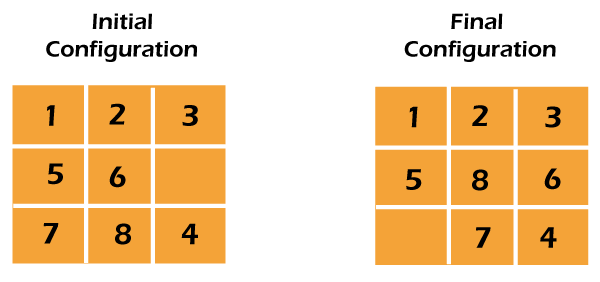
Figure : 8 Puzzle's State Space Tree In this solution, further movements might not always send us closer to the objective, but rather further away. Regardless of the initial state, the state-space tree searches down the leftmost route from the root. With this method, an answer node might never be discovered. 2. BFS (Brute - Force) :We can search the state space tree using a breadth-first approach. It always locates the goal state that is closest to the root. However, the algorithm tries the same series of movements as DFS regardless of the initial state. 3. Branch and Bound :By avoiding searching in sub-trees which do not include an answer node, an "intelligent" ranking function, also known as an approximatsion costs function, may frequently speed up the search for an answer node. However, instead of using the backtracking method, it does a BFS-style search. Basically, Branch and Bound involves three different kinds of nodes.
Costs function :In the search tree, each node Y has a corresponding costs. The next E-node may be found using the costs function. The E-node with the lowest costs is the next one. The function can be defined as : The optimum costs function for an algorithm for 8 puzzles is : We suppose that it will costs one unit to move a tile in any direction. In light of this, we create the following costs function for the 8-puzzle algorithm : There is an algorithm for estimatsing the unknown value of h(y), which is accessible. Final algorithm :
The route taken by the aforementioned algorithm to arrive at the final configuration of the 8-Puzzle from the starting configuration supplied is shown in the diagram below. Keep in mind that only nodes with the lowest costs function value are extended. 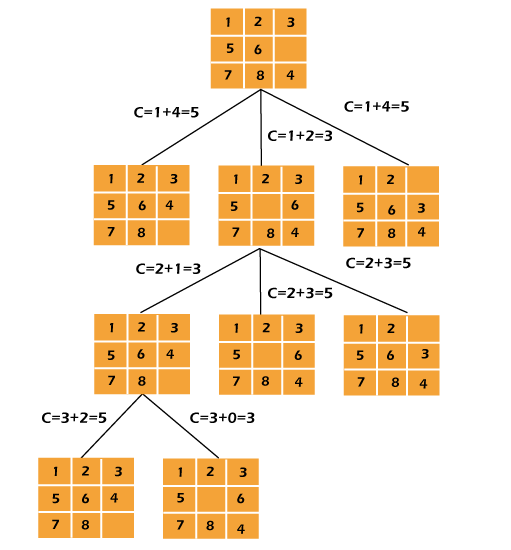
Code :Output: 1 2 3 5 6 0 7 8 4 1 2 3 5 0 6 7 8 4 1 2 3 5 8 6 7 0 4 1 2 3 5 8 6 0 7 4
Next Topicaccuracy_score in Sklearn
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










