Python Variance Function

We can utilize the statistics package's powerful capabilities to calculate any statistic-related task. One of these functions is variance(). We can calculate the data sample's variance with this method's aid (the sample is a small part of population data).

We can use the variance() function when calculating a sample's variance. The variance of the total population can be determined using a different function called pvariance().

The square of the deviation of a quantity from its mean is known as variance in elementary statistics. In essence, it assesses how far random data from the data mean, or median score is spread apart. While a high number would suggest that the supplied set of data is much more split out from the average value, a lower score for a variance would suggest that the data values are grouped around the mean instead of spreading apart.

In science, wherein statistical data analysis is widespread, variance is a crucial tool. It is also referred to as the given data's second central moment and is equal to the square of the dataset's standard deviation. In pure statistics, it is typically expressed as s2, σ2, and Var().

Mathematically variance is the result of the squared mean of the deviation of the individual data points from the mean.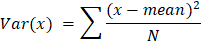

Syntax of the variance function

Parameters

• [data]:-This is an array or any Python iterable data structure that contains real values.
• xbar (Optional): In this parameter, we need to give a real value, the mean of the given dataset.

Return type: This function returns the variance of the dataset given to it.

Example - 1

Code

Output:

The variance of the data sample is:-  0.6397066666666666

Example - 2

Code

Output:

Variance of the Sample_1 is:-  5.238095238095238
Variance of the Sample_2 is:-  3.7666666666666666
Variance of the Sample_3 is:-  61.714285714285715
Variance of the Sample_4 is:-  2549/17280
Variance of the Sample_5 is:-  0.52253

Example - 3

Code

Output:

The variance of the data sample is:-  20.435000000000002

Example - 4

We'll now see that the variance value becomes incorrect if the xbar parameter's value differs from the actual mean or average value.

Code

Output:

The mean of the sample set is:- 
2.5
The correct variance of the sample set is:-  20.435000000000002
The incorrect variance of the sample set is:-  11839.96625

Example - 5

We will see how to when the variance() function will raise the StatisticsError.

Code

Output:

StatisticsError                           Traceback (most recent call last)
<ipython-input-5-d7f3060a7f32> in <module>
      8 
      9 # Passing an empty dataset to the function will raise the StatisticsError
---> 10 print(statistics.variance(sample))

/usr/lib/python3.8/statistics.py in variance(data, xbar)
    739     n = len(data)
    740     if n < 2:
--> 741         raise StatisticsError('variance requires at least two data points')
    742     T, ss = _ss(data, xbar)
    743     return _convert(ss/(n-1), T)

StatisticsError: variance requires at least two data points

Applications of Calculating Variance

Variance is a crucial technique for processing massive quantities of data in statistics. For instance, variance is employed as a biased estimator if the sample mean value (the correct mean) is unknown. Only a limited number of real-life observations may be made, such as the value changes of all corporation stocks during the day. As a result, variance is computed from a limited collection of data; even if it doesn't match when computed with the entire population in mind, it will still provide the user with an estimate sufficient to plan further calculations.