Calculate Moving Averages in Python

In this tutorial, we will learn how to calculate the moving averages of time series data in Python. Moving averages is the statistical measure that refers to a set of average values obtained from the data list of fixed length. These data values are the subset of the total observations in the time series data.

Let us assume that we are given a collection of time series data values of length n, and the window we must consider at any time t is of length k. Then we calculate the moving average values by taking the average of the first k data values, following k data values, and so on. The window remains of the same length throughout the array. We stop the process when the window's higher end coincides with the array's end.

Example

Let us take an example of the time series ts = [1, 2, 3, 6, 7], and we have to calculate the moving averages for a window length k = 3. We will start by calculating the average of the first three terms and store that value in the list of moving averages. This average value corresponds to exactly which data value of the array ts is another topic. Now, we will shift the window by one index such that the window starts from the second element and ends at the fourth element of the array. We will calculate the average and will add it to the list. After repeating this step, one more than the window's higher end will coincide with the end of the array. Hence, the process is complete.

We will see how to implement this algorithm in Python:

Code

# Python program to use the sliding window algorithm to find the moving average

# Time series data values
ts = [1, 2, 3, 6, 8]
k = 3
  
i = 0
# Initializing an empty list for the moving average values
moving_average = []
  
# Looping through the time series data ts and considering a window of length 3
while i < len(ts) - k + 1:
    
    # Storing the elements from i to i + k in a different list to perform necessary operations
    window_array = ts[i : i + k]
  
    # Calculatng the average of the values present in the current window
    average = round(sum(window_array) / k, 2)
      
    # Storing the moving average of the recently executed values in a window in the moving average list
    moving_average.append(average)

    # Displaying the current window and its average
    print(f"Window {i+1} :", window_array, "has an average of:", average)
      
    # Shifting the window to the next index of the array
    i += 1
  
print("The moving averages are:", moving_average)

Output:

Window 1: [1, 2, 3] has an average of: 2.0
Window 2: [2, 3, 6] has an average of: 3.67
Window 3: [3, 6, 8] has an average of: 5.67
The moving averages are: [2.0, 3.67, 5.67]

Simple Moving Average

SMA is the most basic type of moving average. It involves the average of the given k-period values where the values will have a weight equal to 1. Analysts use the SMA to analyze or measure current or future trends. It assumes that the past and the current or the most recent observations have the same contribution in predicting the future trend. We will also see the types of moving averages that counter this assumption.

Formulae of calculating SMA: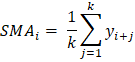

where,

SMA_i is the Simple Moving Average of the ith window

k is the size of the window at any time t

y_{i + j} is the ith value from the set of observations having a lag of j.

Method 1

We will use the Numpy module of Python. The Numpy module simplifies the sum and mean of the array. We will use the sum() function to find the summation of the array elements.

Code

# Python program to calculate the simple moving average using the Numpy module

# Importing the Numpy module
import numpy as np

# Time series data values
ts = [1, 2, 3, 6, 8]

# Period of the moving average
k = 3
  
i = 0
# Initializing an empty list for the moving average values
moving_average = []
  
# Looping through the time series data ts and considering a window of length 3
while i < len(ts) - k + 1:
  
    # Calculatng the average of the values present in the current window
    average = round(np.sum(ts[i : i + k]) / k, 2)
      
    # Storing the moving average of the recently executed values in a window in the moving average list
    moving_average.append(average)

    # Shifting the window to the next index of the array
    i += 1
  
print("The moving averages are:", moving_average)

Output:

The moving averages are: [2.0, 3.67, 5.67]

Method 2

In this method, we will use the Pandas library of Python. This library provides a simpler way to find the simple moving average of the given time series observation data. Pandas has a built method that provides a rolling window of any specified size. We thus have to use this function to get values of different windows. Then we will calculate the average of the values of each window. We will apply another Pandas function on the window-series object to calculate the mean. We cannot apply the rolling function on the Numpy array or a Python data structure. Therefore, we must convert our array to a Pandas series object to apply this function.

Code

# Python program to find the simple moving average using the built-functions of Pandas library

# Importing the required library
import pandas as pd

# Creating the sample time series observations 
ts = [1, 2, 3, 6, 8]

# Specifying the period of moving average
# This is also the window size
k = 3
  
# Converting the array of integers values to a Pandas series object
series = pd.Series(ts)
  
# Getting the windows of the time series data of specified size
# We are using a window size of k
windows = series.rolling(k)
  
# Creating a series of the simple moving averages for each window of the windows object
sma = windows.mean()
  
# Converting the Pandas series to a Python list object
sma_list = sma.tolist()

# The raw moving average list
print("Raw list: ", sma_list)

# Removing the null values from the list
# For the first (k-1) elements of the array, the elements for the window will be less than the window size.
# Therefore, windows for first (k-1) elements will contain null values
list_ = sma_list[k - 1: ]
  
print("The final list of Simple Moving Averages: ", list_)

Output:

Raw list:  [nan, nan, 2.0, 3.6666666666666665, 5.666666666666667]
The final list of Simple Moving Averages:  [2.0, 3.6666666666666665, 5.666666666666667]

Cumulative Moving Average

Another type of moving average is Cumulative Moving Average. To calculate CMA, we first find the cumulative sum of the times series observations. Then we take the cumulative average. This mean is used for the analysis of the time series data.

Formulae: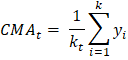

Where:

CMA_t is the Cumulative Moving Average at any time t

K_t is the total number of observations up to the particular time t

y_i is the ith element of the array of the time series data

Method 1

We will first use Numpy to solve this problem. Numpy provides an easy way to find the cumulative sum array. We will first create a Numpy array of the sample data and, with the help of the built-in Numpy function cum_sum(), create the cumulative sum array. When we loop through each value, find the average and store it in the list of moving averages.

Code

# Python program to find the cumulative moving average using the Numpy library

# Importing the required library  
import numpy as np

# Creating the sample time series observations 
ts = [1, 2, 3, 6, 8]
  
i = 1
# Initializing an empty list to store the cumulative moving average
moving_averages = []
  
# Creating an array of the cumulative sum of the time series data
cum_sum = np.cumsum(ts)
print("The cumulative sum of observations: ", cum_sum)
  
# Looping through the cumulative sum array elements
while i <= len(ts):
  
    # Calculating the cumulative average by simply dividing the ith cumulative sum by the total number of observations present till the ith position
    average = round(cum_sum[i-1] / i, 2)
      
    # Storing the cumulative average of the current window in the list of moving averages
    moving_averages.append(average)
      
    # Shifting the window to the right by one index
    i += 1
  
print("The Cumulative Moving Average is: ", moving_averages)

Output:

The cumulative sum of observations:  [ 1 
3  6 12 20]
The Cumulative Moving Average is:  [1.0, 1.5, 2.0, 3.0, 4.0]

Method 2

We will use the Pandas library this time. Pandas library also provides a built-in function to calculate the cumulative sum of the array of observations. Its function Series.expanding() spans over all observations with a window size of [1, length(array)]. Though it does not provide the sum, it will only return the n windows in the range[1, n] where n = length(array). We will use the Series.mean() function to find the mean of observations of each window.

Code

# Python program to calculate the cumulative moving averages using built-in functions of the pandas library

# Importing the required library
import pandas as pd
  
# Creating the sample time series observations 
ts = [1, 2, 3, 6, 8]

# Specifying the period of moving average
# This is also the window size
k = 3
  
# Converting the array of integers values to a Pandas series object
series = pd.Series(ts)
  
# Getting the windows of the pandas series of observations 
windows = series.expanding()
  
# Creating a series of the simple moving averages for each window of the windows object
sma = windows.mean()
  
# Converting the Pandas series to a Python list object
sma_list = sma.tolist()
  
print("The Cumulative Moving Average is: ", sma_list)

Output:

The Cumulative Moving Average is:  [1.0, 1.5, 2.0, 3.0, 4.0]

Exponential Moving Average

Another type of moving average is Exponential Moving Average. We calculate EMA by taking the weighted mean of the time series data. The difference between an EMA and a WMA is that the weights in EMA decrease exponentially with time. Hence it is Exponential Moving Average. This type of moving average is very fast at catching the trends. It is faster because it is slightly more sensitive to the fluctuation or changes in the observations over the course of the period we are studying. This property makes EMA efficient for short-term analysis of time series data.

Formulae: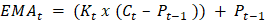

EMA_t is the exponential moving average for the observation at time t

K_t is the exponential smoothing constant for the tth observation

C_t is the value of the observation at time t

P_{t - 1} is the EMA of the time period t - 1

Method 1

We will solve this problem by writing our own algorithm to find the EMA of a given time series.

Code

# Python program to design an algorithm to find the EMA

# Importing the numpy module
import numpy as np

# Creating the sample time series observations 
ts = [1, 2, 3, 6, 8]
x = 0.28  # the exponential smoothening factor
  
i = 1
# Initializing an empty list to put the EMA values
moving_averages = []
  
# Inserting the first exponential moving average in the list
moving_averages.append(ts[0])
  
# Looping through the elements of the array
while i < len(ts):
  
    # Calculating the exponential moving average using the formula we stated
    average = round(x * (ts[i] - moving_averages[-1]) + moving_averages[-1], 2)
      
    # Storing the cumulative average of the current window of elements in the moving_averages list
    moving_averages.append(average)
      
    # Shifting the window to the right by one index
    i += 1
  
print("The EMA values are: \n", moving_averages)

Output:

The EMA values are: 
 [1, 1.28, 1.76, 2.95, 4.36]

Method 2

We will use the Pandas library to calculate the EMA in this example. The Pandas library provides a built-in method Series.ewm(com). This method is designed to find a Pandas Series of the exponentially weighted windows out of the given Series of data. We have to give a com value to the function. According to the formula above, K = 1 / (1 + com). This way, the weights will be calculated by the function and multiplied by the time series data to which we have attached the function. The value of K always lies between 0 and 1.

Code

# Python program to find EMA using the Pandas library

# Importing the Pandas module
import pandas as pd

# Creating the sample time series observations 
ts = [1, 2, 3, 6, 8]

# The exponential smoothening factor
K = 0.28  

# Calculating the value of the com parameter
com = (1 - K) / K
  
# Converting the list into a Pandas Series object
ts_series = pd.Series(ts)

# Calculating the EMA using the ewm() method and passing the com value to it.
ew_window = ts_series.ewm(com = 2.5)

# Finding the mean of each window
ema = ew_window.mean()

# Converting the ema Series object to Python List object
ema_list = ema.tolist()

print("The list of Exponential Moving Averages: ", ema_list)

Output:

The list of Exponential Moving Averages: [1.0, 1.5833333333333333, 2.220183486238532, 3.6801801801801797, 5.196316328022218]

Weighted Moving Average (WMA)

Some analysts argue that the most recent values add more importance to measuring a trend through a time series than the older data. Thus they created Weighted Moving Average. The calculation of WMA is almost the same as SMA. The main difference is that the data will be multiplied with the pre-defined weights here.

The weights should follow some conditions:

The weights should always add up to 1
The weights should be in increasing order according to the time series. That is, recent data will have more weight than the previous data.

Formulae of calculating WMA: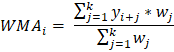

Where,

WMA_i is the Weighted Moving Average of the ith window

k is the size of the window at any time t

y_{i + j}is the ith value from the set of observations having a lag of j.

w_j is the weight of the jth observation of the window

Method 1

We will first use the Numpy module of Python. We will use the same logic as we used to calculate SMA. The difference is that we will simultaneously loop through the weights array and, leveraging the elementwise multiplication of Numpy arrays, multiply the data to the weights. Then we will find the sum of the multiplied series and the sum of the current window of weights. On dividing these two numbers, we will get the weighted mean of the current window.

Code

# Python program to calculate the weighted moving average using the Numpy module

# Importing the Numpy module
import numpy as np

# Time series data values
ts = np.array([1, 2, 3, 6, 8])

# Creating a list of the weights
w = np.array([1/15, 2/15, 3/15, 4/15, 5/15])

# Period of the moving average
k = 3
  
i = 0
# Initializing an empty list for the weighted moving average values
moving_average = []
  
# Looping through the time series data ts and weights simultaneously 
while i < len(ts) - k + 1:

    # Window of the time seires
    ts_window = ts[i : i + k]

    # Window of the weights
    w_window = w[i : i + k]

    # Finding the weighted series
    ws = ts[i : i + k] * w[i : i + k]

    # Calculatng the average of the values present in the current window
    average = round(np.sum(ws) / np.sum(w_window), 2)
      
    # Storing the weighted moving average in the list
    moving_average.append(average)

    # Shifting the window to the next index of the array
    i += 1
  
print("The weighted moving averages:", moving_average)

Output:

The weighted moving averages: [2.33, 4.11, 6.08]

Method 2

In this method, we will use the Pandas library of Python. This library provides a simpler way to find the simple moving average of the given time series observation data. Pandas has a built method that provides a rolling window of any specified size. We thus have to use this function to get values of different windows. Then we will calculate the average of the values of each window. We will apply another Pandas function on the window-series object to calculate the mean. We cannot apply the rolling function on the Numpy array or a Python data structure. Therefore, we need to convert our array to a Pandas series object to apply this function.

Code

# Python program to find the simple moving average using the built-functions of Pandas library

# Importing the required library
import pandas as pd

# Creating the sample time series observations 
ts = [1, 2, 3, 6, 8]

# Specifying the period of moving average
# This is also the window size
k = 3
  
# Converting the array of integers values to a Pandas series object
series = pd.Series(ts)
  
# Getting the windows of the time series data of specified size
# We are using a window size of k
windows = series.rolling(k)
  
# Creating a series of the simple moving averages for each window of the windows object
sma = windows.mean()
  
# Converting the Pandas series to a Python list object
sma_list = sma.tolist()

# The raw moving average list
print("Raw list: ", sma_list)

# Removing the null values from the list
# For the first (k-1) elements of the array, the elements for the window will be less than the window size.
# Therefore, windows for first (k-1) elements will contain null values
list_ = sma_list[k - 1: ]
  
print("Final list of Simple Moving Averages: ", list_)

Output:

Raw list:  [nan, nan, 2.0, 3.6666666666666665, 5.666666666666667]
The final list of Simple Moving Averages:  [2.0, 3.6666666666666665, 5.666666666666667]

Applications

Time-Series Analysis: It smooths out short-term variation and highlights long-term observations such as trends and cycles.

Financial Analysis: It is used in financial analysis of stock markets, like the calculation of stock prices and returns and analyzing trends of the market.

Environmental Engineering: It is used in analyzing environmental conditions by considering various factors such as the concentration of pollutants, etc.

Computer Performance Analysis: It is used to analyze computer performance by calculating metrics such as average CPU utilization, process queue length, etc.

Next TopicExponential Moving Average in Python

← prev next →