Python Tutorial
Python OOPs
Python MySQL
Python MongoDB
Python SQLite
Python Questions
Plotly
Python Tkinter (GUI)
Python Web Blocker
Python MCQ
Related Tutorials
Python Programs
Log Normal Distribution in Statistics Using PythonThe scipy.stats.lognorm() describes the Log-Normal continuous random variable. It is an instance of the rv_continuous class inherited from the generic methods. It completes the techniques by adding details specific to this distribution. The Probability Density Function, which gives the Log-Normal Distribution, is given by: 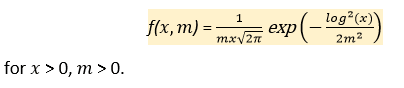
The probability density function for log-normal distribution defined is the standardized form. We use the loc and scale parameters to shift and scale the distribution. The shifting of the location does not make it a noncentral distribution. lognorm.pdf(x, loc, scale) is exactly equal to lognorm.pdf(y, m) / scale with y = (x - loc) / scale. The lomax is a special Pareto case with a loc value = 1.0. Parameters including in the Lomax Distribution
By default, it is 'mv' (mean and variance)
Python provides the lognorm module under the scipy.stats library, which is used to find the log-normal Distribution. Importing the lognorm() library in PythonLet's understand the concept of log-normal Distribution in Statistics with the help of different programs in Python. Program 1: A program to create Log Normal Distribution Random Variable Code: Output: Random Variable : <scipy.stats._distn_infrastructure.rv_continuous_frozen object at 0x000001B8B0959750> Explanation: Using the lognorm() function, we have made a Log-Normal distribution random variable. Firstly, we imported the lognorm module and assigned two variables, x, and y, with random values. Then using the lognorm function, we created the random variable. Program 2: A program to create Log Normal continuous variates and its Probability distribution. Code: Output: Random Variates : 5.464299313307819 Probability Distribution : [0.02646144 0.02731563 0.02822343 0.02918999 0.03022114 0.03132348 0.03250455 0.03377301 0.0351388 0.03661346] Explanation: We have created the random variates using lognorm.rvs() function and the probability distribution using the lognorm.pdf() function using a numpy array with random values. Program 3: A program to graphically represent the Log Normal Probability distribution. Code: Output: Distribution : [0. 0.10204082 0.20408163 0.30612245 0.40816327 0.51020408 0.6122449 0.71428571 0.81632653 0.91836735 1.02040816 1.12244898 1.2244898 1.32653061 1.42857143 1.53061224 1.63265306 1.73469388 1.83673469 1.93877551 2.04081633 2.14285714 2.24489796 2.34693878 2.44897959 2.55102041 2.65306122 2.75510204 2.85714286 2.95918367 3.06122449 3.16326531 3.26530612 3.36734694 3.46938776 3.57142857 3.67346939 3.7755102 3.87755102 3.97959184 4.08163265 4.18367347 4.28571429 4.3877551 4.48979592 4.59183673 4.69387755 4.79591837 4.89795918 5. ] 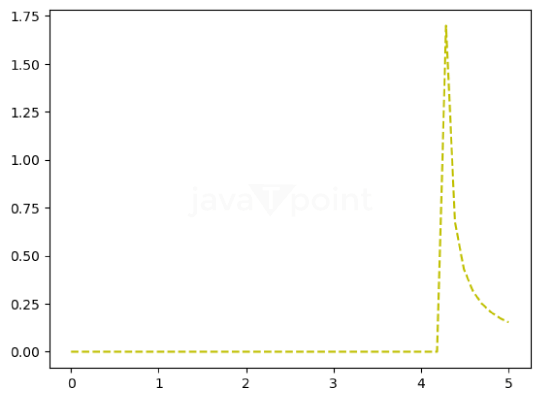
Explanation: We have printed the distribution using the numpy array, and then using matplotlib, we have printed a graph of the Log-normal Distribution using the Probability Density function. Program 4: A program to graphically represent varying positional arguments in the Log Normal Probability Distribution Function. Code: Output: [ 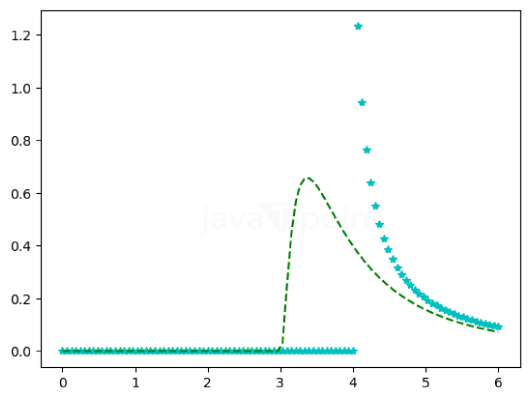
Explanation: We made a numpy array with linear, equal spaces, then plotted a graph with two different Log normal distributions using the Probability Density Functions. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









