Introduction to Trie using Python

A tree-based information structure called a "Trie" is portrayed as being utilized to store assortments of strings and complete speedy pursuits on them. The name "Trie" comes from the action word "Recovery," which indicates the demonstration of finding or securing something.

Two strings will have a similar precursor in the Trie if they share a prefix, per a standard that the Trie keeps. A trie might be utilized to look on the off chance that a string with a particular prefix is available in the Trie or not, as well as to sort an assortment of strings sequentially.

Need for Trie Data Structure?

A Trie information structure is utilized for information capacity and recovery; comparable exercises could be done utilizing a Hash Table information structure. Be that as it may, Trie is more successful at completing these undertakings. Furthermore, Trie has an advantage over the Hash table of its own. Prefix-based looking should be possible with a Trie information structure; notwithstanding, utilizing a Hash table is impossible.

A Trie's fundamental structure is a tree-like arrangement in which each Node stands for a single letter or segment of a string. As you move down the tree, characters are added to create whole words or phrases starting at the root node, representing an empty string. Fast and accurate string-based operations are possible because of this hierarchical organization.

The Trie's capacity to quickly complete tasks like looking for words with a similar prefix or identifying all terms in a dictionary that meet a specific pattern is one of its distinguishing qualities. Tries are incredibly effective for jobs requiring enormous collections of strings since these operations have a temporal complexity dependent on the query string's length rather than the dataset's size.

Additionally, Tries are used in dictionary and autocomplete functions, which enhance user experience in programs like chat platforms, code editors, and search engines. Their effective prefix-matching capabilities enable real-time suggestions, improving the usability and effectiveness of user interactions.

There are other types of Tries, such as the regular Trie, compressed Trie, and ternary search Trie, each of which is intended to optimize a particular use case. For example, compressed tries minimize space complexity by combining common prefixes, while ternary search tries are excellent at effectively managing large vocabulary.

Attempts have many uses, including IP routing, spell-checking, and natural language processing. Understanding Tries continues to be essential for improving the speed and accuracy of text-related computations and optimizing string-based algorithms.

Tries are a crucial data structure that enables effective string-based operations to sum up. Thanks to their adaptability and speed in various applications, they improve the performance of systems that rely on string matching, searching, and indexing. The power of Tries can be harnessed, and algorithms can be optimized for text-related activities in the ever-expanding field of computer science and information technology, but understanding Tries is essential.

Trie's information structure enjoys a few upper hands over a hash table.

The A trie information structure is better than a hash table in the accompanying ways:

Trie takes into consideration compelling prefix search (or auto-complete).
We can undoubtedly print each word in sequential request, which hashing makes troublesome.
In a Trie information structure, hash capabilities have no above.
Indeed, even with a major assortment of strings in a Trie information structure, looking for a string just requires O(L) time intricacy, where L is the number of words in the pursuit term. On the off chance that the question string is excluded from the Trie, the inquiry time might try and be not exactly O(L).

Properties of a Trie Data Structure

We realize that Trie is coordinated like a tree. Along these lines, understanding its characteristics is essential.

A few vital qualities of the Trie information structure are recorded below:

Thus, every hub requires 26 pointers, where the 0th record signifies the letter "a" and the 25th file indicates the person "z."
A word or string is addressed in every way, from the root to a specific hub.
Here is a direct Trie information structure model.
Each Trie contains a solitary root hub.
A trie's hubs relate to strings, while its edges relate to characters.
Every hub comprises a hashmap or a variety of pointers, where each list is a person and a banner signifies on the off chance that the hub is the finish of any strings.
Any measure of characters, including alphabetic, numeric, and unique characters, can be utilized in a Trie information structure. However, here, we'll zero in on strings that contain the letters a through z.

Trie Information Design: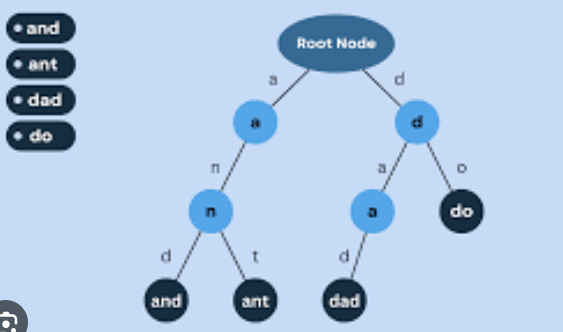

How Can Trie Data Structure Work?

We know that any measure of characters, including letter sets, numerals, and extraordinary characters, might be utilized in the Trie information structure. In any case, here, we'll zero in on strings that contain the letters a through z. Hence, every hub requires 26 pointers, where the 0th file means the letter "a" and the 25th record indicates the person "z."

Any lowercase English word might start with one of the letters beginning to end, trailed by one of the letters a to z again for the word's third letter, etc. To store a word, we should utilize a cluster (compartment) of size 26. Since there are no words from the outset, the characters in the cluster are all vacant, as seen underneath.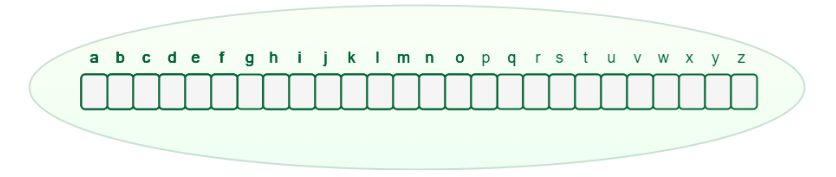

We should perceive how the Trie information structure stores the words "and" and "subterranean insect":

1. In the Trie information construction, store "and":

Since "and" starts with "a," we will mark the spot "a" in the Trie hub as filled, connoting the utilization of "a."
After embedding the principal character, there are 26 choices for the subsequent person, meaning that "a" again has a 26-character cluster of its own for putting away the subsequent person.
Since "n" is the subsequent person, we will go from "a" to "n" and imprint "n" in the subsequent cluster as used.
Mark the area "d" as used in the proper cluster as "d" comes later "n" as the third person.

2. In the Trie data structure, store "ant":

The root node already has an "a" because the word "ant" begins with that letter. Therefore, it is unnecessary to fill it out again; simply move to Trie node 'a'.
For the second character, 'n,' we can see that the space in the 'a' node for 'n' has already been taken. So there is no need to fill it again; simply move to Trie node 'n'.
The 't' slot in the 'n' node is empty for the final character of the word, which is a 't'. To advance to the 't' node, fill the place of 't' in the 'n' node.

The Trie will appear as follows after the words "and" and "and" have been stored: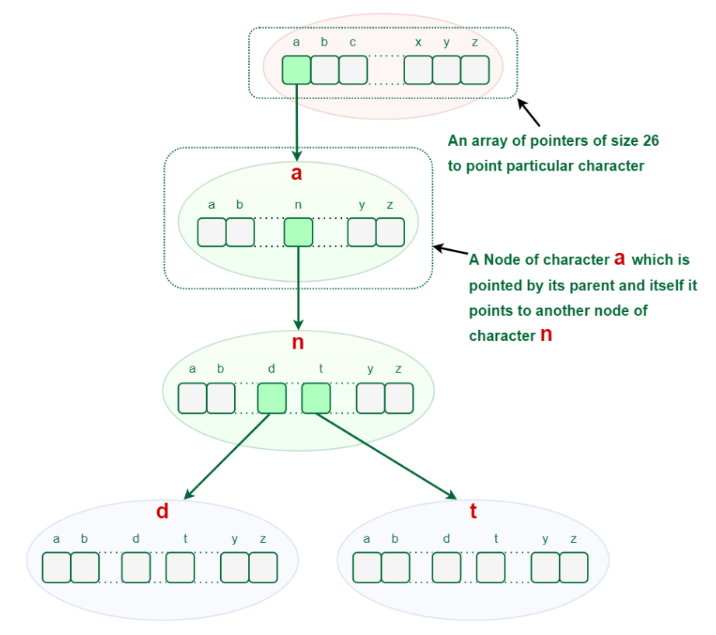

Representation for a Trie Node:

Each Trie node comprises a character pointer array or hashmap and a flag indicating whether or not the word ends at that Node. But rather than using a hashmap to create Trie Node, we may use an array if the words only include lowercase letters (i.e., a-z).

# Python code
class TrieNode:
    # Trie node class
    def _init_(self):
        self.children = [None for _ in range(26)]
        # The amount of strings that are
        # stored in the Trie from the root node to any Trie node will be tracked by this.
        self.wordCount = 0 

Basic Trie Data Structure Operations:

Insertion
Search
Deletion

1. Trie Data Structure Insertion:

This operation adds new strings to the Trie data structure. Let's test this out first:

Let's try adding "and" and "ant" to this sentence: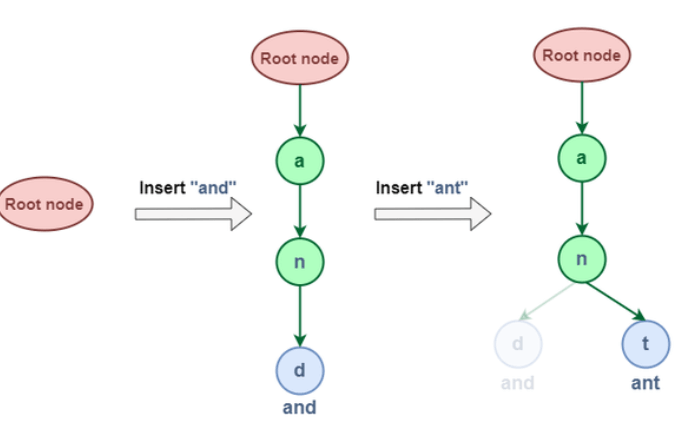

The word "and" and "ant" have a common node (i.e. "an") in the insertion representation shown above. This is due to the Trie data structure's characteristic that if two strings share a prefix, they will have the same ancestor.

Let's try inserting "dad" and "do" now: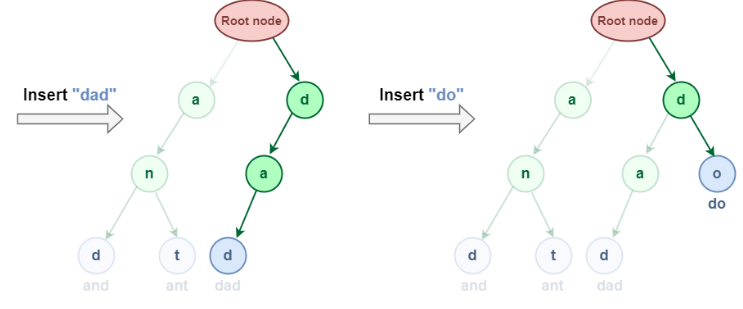

Insertion implementation in the Trie data structure:

Algorithm:

Make the capability embed (TrieNode *root, string &word), which will acknowledge two contentions: the root and the string to be embedded into the Trie information structure.
Then, introduce another pointer named currentNode with the root hub.
Check if the worth in the variety of pointers at the ongoing person of the string is Invalid or not, as you emphasize over the length of the given string.
- Make another hub if It Is Invalid, and allude the ongoing person to this new hub.
- Move the curr to the fresh out of the plastic new hub.
The word count of the last currentNode should then be expanded, showing that currentNode is the finish of a string.

The following is the execution of the above calculation:

def insert_key(root, key):
    # Set the root node as the current node pointer's initial value.    currentNode = root
    # iterate over the string's length
    for c in key:
        # Verify the existence of the Node for the current
        # the Trie character.
        if currentNode.childNode[ord(c) - or('a')] == None:
            # If the Node for the current character is missing, create a new node.
            newNode = TrieNode()
            # Keep the reference for the 
            # node that was just formed.
            currentNode.childNode[ord(c) - ord('a')] = newNode
        # Transfer the current node pointer to the newly generated Node.
        currentNode = currentNode.childNode[ord(c) - or('a')]
    # WordEndCount for the most recent current Node is increased.
    # pointer This suggests that a string with an ending of 
   # currentNode exists.
    currentNode.wordCount += 1

2. Trie Data Structure search:

The main way the pursuit activity varies from the addition activity in Trie is that at whatever point we find that the variety of pointers in the curr hub doesn't highlight the ongoing person of the word, we return misleading instead of making another hub for that person.

Utilizing this strategy, you might check whether a string is put away in the Trie information structure. The Trie information structure has two different pursuit techniques.

look at Trie to check whether the provided word is there.
look at Trie to see whether any words with the predetermined prefix are available.

The two techniques utilize a comparable inquiry design. Changing a word over completely to letters and contrasting every one and a trie hub from the root hub are the underlying strides in a Trie look for a given word. Proceed to the hub's kids, assuming the ongoing person is tracked down there. Keep doing this until all characters are found.

2.1 Trie Data Structure Prefix Search: Look for the prefix "an" in the Trie Data Structure.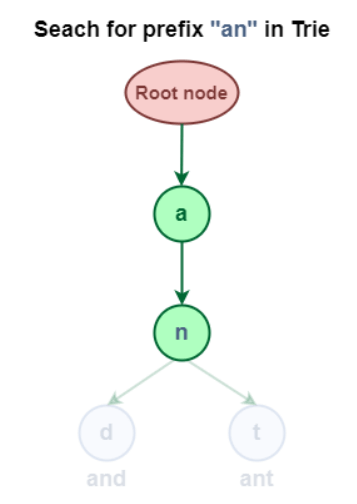

Prefix Search implementation in the Trie data structure:

def is_prefix_exist(root, key):
    # Set the root node as the current node pointer's initial value.
    current_node = root
    # iterate over the string's length
    for c in key:
        # Verify if the Node for the current 
        # character in the Trie exists.
        if current_node.child_node[ord(c) - or('a')] is None:
            # There isn't a given word prefix in Trie.
            return False
        # Transfer the currentNode reference to the current character's 
       # existing Node.
        current_node = current_node.child_node[ord(c) - or('a')]
  # Prefix exists in the Trie
    return True

2.2 Complete word search in the Trie Data Structure:

It is similar to prefix search, but we must also determine if the word ends at the final character.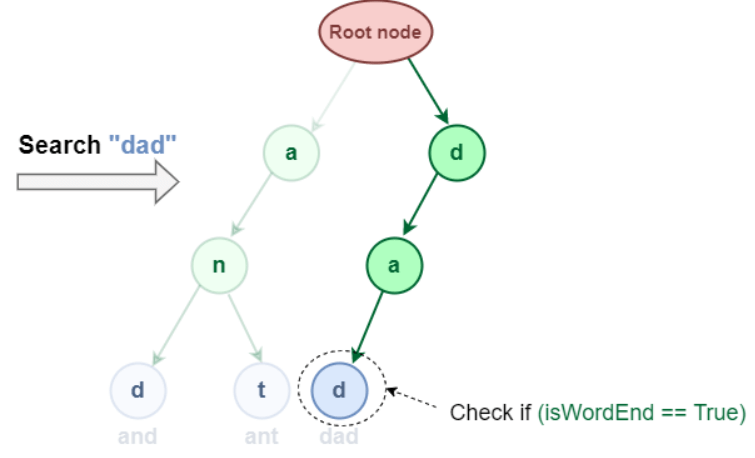

Using the Search algorithm with the Trie data structure:

def search_key(root, key):
    # Set the root node as the current node pointer's initial value.
    currentNode = root  
    # iterate over the string's length
    for c in key:
        # Verify if there is a node for the character you see in the Trie.
        if currentNode.childNode[ord(c) - or('a')] is None:
            # In Trie, the given word doesn't exist.
            return False
  
        # Transfer the current node reference to the current character's existing Node.
        currentNode = currentNode.childNode[ord(c) - or('a')]  
    # If the word count is more than 0, return it.
    return currentNode.wordCount > 0

3. Trie Data Structure Deletion

Strings can be removed from the Trie data structure using this method. When removing a word from Trie, there are three scenarios.

The deleted word functions as a prefix for other Trie words.
The word eliminated has a prefix in common with other words in Trie.
There is no prefix that the removed word has in common with other words in Trie.

Example:

3.1 The removed word functions as a prefix for additional Trie words.

The deleted word "an," as seen in the accompanying graphic, shares a full prefix with the words "and" and "ant."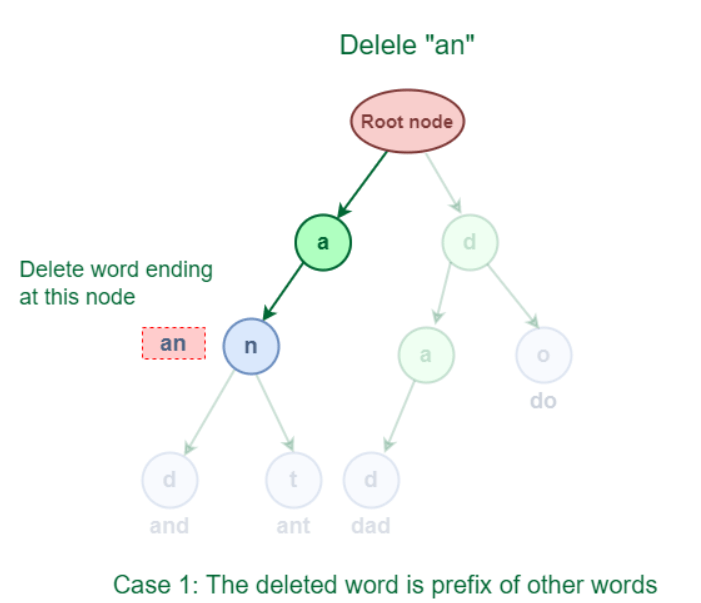

Reducing the word count by 1 at the word's ending Node will execute a delete operation in this situation.

3.2 The eliminated word has a prefix in common with other words in Trie.

As seen in the accompanying image, the deleted word "and" has several prefixes, with other words beginning with "ant." They both start with "an."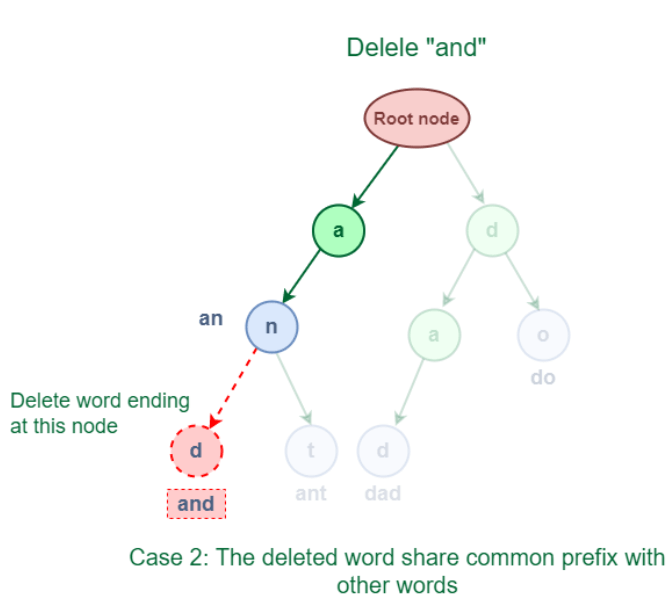

3.3 There is no prefix that the deleted word has in common with any other Trie terms.

As seen in the accompanying diagram, the term "java" does not share a common prefix with any other words.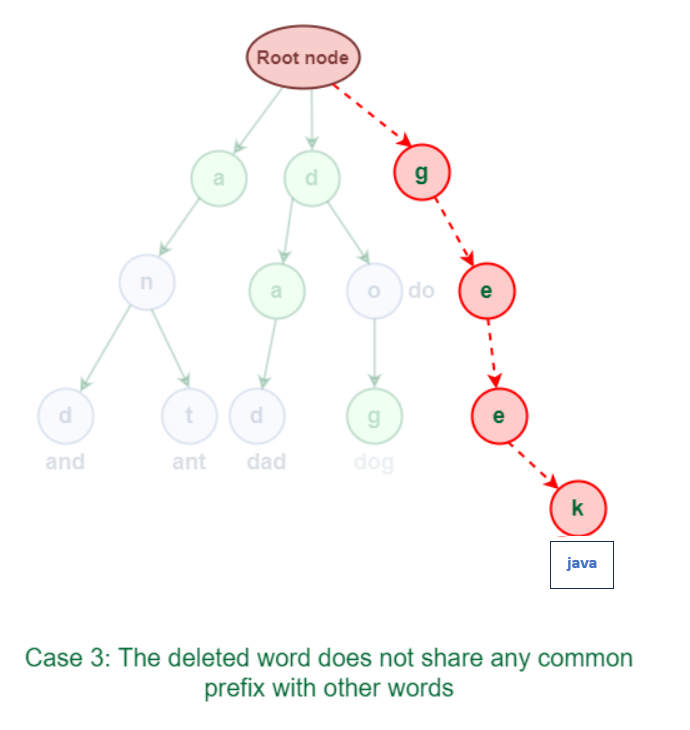

Simply deleting every Node will solve the problem in this instance.

The implementation that manages all the circumstances mentioned above is shown below:

def delete_key(root, word):
    current_node = root
    last_branch_node = None
    last_branch_char = 'a' 
    # iterate over each letter in the word
    for c in word:
        # Unless the current character is a child of the current Node,
        # Because the term is absent from Trie, return False.
        if current_node.childNode[ord(c) - or('a')] is None:
            return False
        else:
            count = 0
            # count how many offspring the current Node has.
            for i in range(26):
                if current_node.childNode[i] is not None:
                    count += 1
            # save the Node and the current character if the number of children exceeds 1.
            if count > 1:
                last_branch_node = current_node
                last_branch_char = c
              current_node = current_node.childNode[ord(c) - or('a')]
      count = 0
    # count how many offspring the current Node has.
    for i in range(26):
        if current_node.childNode[i] is not None:
            count += 1  
    # Case 1: The removed word functions as a prefix for other Trie words.
    if count > 0:
        current_node.wordCount -= 1
        return True 
    # Case 2: The eliminated word has a prefix in common with other words in Trie.
    if last_branch_node is None:
        last_branch_node.childNode[ord(last_branch_char) - ord('a')] = None
        return True
    # Case 3: Trie has no common prefix between the removed word and any other words.
    else:
        root.childNode[ord(word[0]) - or('a')] = None
        return True

How is the Trie Data Structure implemented?

Use the TrieNode() constructor to create a root node.
Save a group of strings in a vector of strings called arr that we will use to put the strings into the Trie.
Using the insert key() method to insert each string into Trie,
The search_key() method may be used to search strings from search query strings.
With the aid of delete_key, remove the strings from deleteQueryStrings.

# Trie implementation in Python   
class TrieNode:
    def __init__(self):
        # pointer array for each Node's children
        self. child node = [None] * 26
        self.wordCount = 0          
def insert_key(root, key):
    # Set the root node as the current node pointer's initial value.
    currentNode = root
    # iterate over the string's length
    for c in key:
        # Verify if the Node for the selected character in the Trie exists.
        if not currentNode.childNode[ord(c) - or('a')]:
            # If there is no node for the current character
            # Then make a new node
            newNode = TrieNode()
            # Keep the Node's reference that was just formed.
            currentNode.childNode[ord(c) - ord('a')] = newNode
        # Transfer the current node pointer to the brand-new Node at this moment.
        currentNode = currentNode.childNode[ord(c) - or('a')]
    # WordEndCount for the most recent currentNode is an increased pointer 
   # This suggests that currentNode has a string at its conclusion.
    currentNode.wordCount += 1
def search_key(root, key):
    # Set the root node as the currentNode pointer's initial value.
    currentNode = root
    # iterate over the string's length
    for c in key:
        # Verify if the Node for the selected character in the Trie exists.
        if not currentNode.childNode[ord(c) - or('a')]:
            # In Trie, the given word doesn't exist.
            return False
        # Transfer the currentNode reference to the current character's existing Node.
        currentNode = currentNode.childNode[ord(c) - or('a')]
    return currentNode.wordCount > 0 
def delete_key(root, word):
    currentNode = root
    lastBranchNode = None
    lastBrachChar = 'a'  
    for c in word:
        if not currentNode.childNode[ord(c) - ord('a')]:
            return False
        else:
            count = 0
            for i in range(26):
                if currentNode.childNode[i]:
                    count += 1
            if count > 1:
                lastBranchNode = currentNode
                lastBrachChar = c
            currentNode = currentNode.childNode[ord(c) - ord('a')]  
    count = 0
    for i in range(26):
        if currentNode.childNode[i]:
            count += 1  
    # Case 1: The deleted word functions as a prefix for other Trie words.
    if count > 0:
        currentNode.wordCount -= 1
        return True  
    # Case 2: The eliminated word has a prefix in common with other words in Trie.
    if lastBranchNode:
        lastBranchNode.childNode[ord(lastBrachChar) - ord('a')] = None
        return True
    # Case 3: There is no prefix that the removed word has in common with other words in Trie.
    else:
        root.childNode[ord(word[0]) - or('a')] = None
        return True
# Driver Code
if __name__ == '__main__':
    # Create a Trie root node.
    root = TrieNode() 
    # Contains the strings that we wish to add to the Trie.
    input_strings = ["and", "and", "do", "java", "dad", "ball"]
    # number of Trie insert procedures
    n = len(input_strings)
    for i in range(n):
        insert_key(root, input_strings[i])
    # stores the strings we wish to search for in the Trie database.
    search_query_strings = ["do", "java", "bat"]  
    # amount of searches conducted in Trie
    search_queries = len(search_query_strings)  
    for i in range(search_queries):
        print("Query String:", search_query_strings[i])
        if search_key(root, search_query_strings[i]):
            # The Trie contains the query string
            print("The query string is present in the Trie")
        else:
            # The Trie does not contain the query string.

            print("The query string is not present in the Trie")
    # saves the strings from the Trie that we wish to remove.
    delete_query_strings = ["java", "tea"]
    # amount of deletions made using the Trie
    delete_queries = len(delete_query_strings)
    for i in range(delete_queries):
        print("Query String:", delete_query_strings[i])
        if delete_key(root, delete_query_strings[i]):
            # The Trie successfully deletes the queryString.
            print("The query string is successfully deleted")
        else:
            # The Trie does not contain the query string.
            print("The query string is not present in the Trie")

Output:

Query String: do
The query string is present in the Trie
Query String: java
The query string is present in the Trie
Query String: bat
The query string is not present in the Trie
Query String: java
The query string is successfully deleted
Query String: tea
The query string is not present in the Trie

Analysis of the Trie Data Structure's Complexity

Operation	Time Complexity	Auxiliary Space
Insertion	O(n)	O(n*m)
Searching	O(n)	O(1)
Deletion	O(n)	O(1)

Note: In the complexity chart above, "n" and "m" stand for the string length and the quantity of strings kept in the Trie, respectively.

Applications of the Trie data structure include:

1. Autocomplete Feature: The autocomplete feature offers suggestions depending on the search terms you enter. The autocomplete feature is implemented using the trie data structure.

2. Spell checkers: They offer suggestions based on what you entered if the term does not appear in the dictionary.

There are 3 steps to it, which are as follows:

Searching the data dictionary for the term.
Making possible recommendations.
Putting recommendations in order of more priority at the top.

Trie saves the dictionary data, facilitates the development of search algorithms for dictionary terms, and offers a list of acceptable words for suggestion.

3. Maximum Prefix Length Match: It is often known as the longest prefix-matching algorithm and is a routing technique used in IP networking. Contiguous masking, which limits search time complexity to O(n), is necessary for network route optimization. n is the length of the URL address in bits.

Multiple Bit Trie methods were created to expedite the search process by doing multiple-bit lookups more quickly.

Advantages of Trie Data Structure:

Benefits of the Trie data structure include its ability to enter strings and locate them in O(l) time, where l is the length of a single word. When compared to binary search trees and hash tables, it is quicker.
It makes it simpler to print all words in alphabetical order by providing alphabetical filtering of entries by the node key.
Trie requires less storage than BST since each key needs a predetermined amount of amortized space to be stored rather than explicitly recorded.
The trie data structure makes it possible to do prefix search and longest prefix matching effectively.
Trie are often quicker than hash tables for short keys like integers and pointers since they don't require a hash function for their implementation.
Tries allow for ordered iteration, but hash tables only allow pseudorandom, typically more laborious, iteration determined by the hash function.
The simple deletion algorithm has a temporal complexity of O(l), where l is the length of the word to be eliminated.

Disadvantages of Trie Data Structure:

The biggest drawback of the trie data structure is that it requires a lot of memory to store all the strings. We have an excessive number of node pointers for each Node, which, in the worst-case scenario, equals the number of letters.
When a hash table is built effectively (i.e., with a suitable hash function and an acceptable load factor), the lookup time is O(1), which is much quicker than O(l) for a trie, where l is the length of the string.

Next TopicK'th Largest Element in BST Using Constant Extra Space Using Python

← prev next →