Symmetric Difference of Multiple Sets in Python

This article will discuss the problem of finding the symmetric difference of multiple sets in Python using various methods.

Sets in Python

In Python, a set is an unordered, mutable collection of unique elements enclosed in curly braces {}. Each element in a set must be hashable, meaning it can be uniquely identified, and immutable, meaning it cannot be changed after it is added to the set. Sets are commonly used for tasks that require membership testing, deduplication, and unordered collections.

Symmetric difference

The symmetric difference between two sets refers to a set that contains elements present in either a set or not present in both sets. In other words, it is the collection of items specific to each set, eliminating the items shared by both sets.

The symmetric difference between two sets can easily be found using the ^ (caret) operator or the symmetric_difference() method.

An example to find the symmetric difference between two sets is as follows:

# Define two sets
set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}

# Compute symmetric difference using the caret operator
sym_diff = set1 ^ set2

# Print the symmetric difference
print("Symmetric Difference:", sym_diff)

# Output
# Symmetric Difference: {1, 2, 3, 6, 7, 8}

# Compute symmetric difference using symmetric_difference() method
sym_diff = set1.symmetric_difference(set2)

# Print the symmetric difference
print("Symmetric Difference:", sym_diff)

# Output
# Symmetric Difference: {1, 2, 3, 6, 7, 8}

The symmetric difference between set1 and set2 contains elements {1, 2, 3, 6, 7, 8} that are present in either set1 or set2, but not in both.

Note: The original sets, set1 and set2 are not modified during the computation of symmetric difference. Instead, a new set containing the result is returned.

Symmetric difference of multiple sets:

In Python, there are various methods to compute the symmetric difference of multiple sets:

For Example:

If the input is:

set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}
set3 = {5, 6, 7, 8, 9}
set4 = {6, 7, 8, 9, 10}

The output should be:

Symmetric Difference: {1, 2, 3, 10}

Explanation - 1, 2, and 3 are present in the set1 only, and 10 is present in the set4 only.

Let us now discuss the various method to find the symmetric difference between multiple sets:

Method 1 - Using Counter from Collections:

In Python, you can compute the symmetric difference of multiple sets by using the Counter from Collections module:

# Importing Counter from collections
from collections import Counter
# Importing chain from itertools
from itertools import chain

# Define sets
set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}
set3 = {5, 6, 7, 8, 9}
set4 = {6, 7, 8, 9, 10}

# Merging all sets into a single iterable.
single__iter = chain(set1, set2, set3, set4)

# Finding the number of occrences of each element
occurrence = Counter(single__iter)

# Finding the elements that has frequency count = 1
set_diff = set([i for i in occurrence if occurrence[i] == 1])

# Printing the set difference
print(f"Set difference: {set_diff}")

Output:

Set difference: {10, 1, 2, 3}

Explanation:

The Counter class takes only one argument (an iterable). But we have four sets, and for that, we have used the chain function from itertools to merge all the sets into a single iterable and pass it to the Counter class to count the occurrences of each element.

The syntax for the chain function is: itertools.chain(*iterables)

# Merging all sets into a single iterable.
single__iter = chain(set1, set2, set3, set4)
print("Single Iter:", *single__iter)

Output:

Single Iter: 1 2 3 4 5 4 5 6 7 8 5 6 7 8 9 6 7 8 9 10

Counter - Counter is a built-in class in the collections module of Python that offers a practical method for counting the number of times an element appears in a collection, such as a list, tuple, or string. It is made specifically for counting occurrences and is a subclass of the dict class.

The syntax for Counter is as follows: collections.Counter([iterable-or-mapping])

# Finding the number of occurrences of each element
occurrence = Counter(single__iter)
print("Each element with frequency:", occurrence)

Output:

Each element with frequency: Counter({5: 3, 6: 3, 7: 3, 8: 3, 4: 2, 9: 2, 1: 1, 2: 1, 3: 1, 10: 1})

# Finding the elements that has frequency count = 1
set_diff = set([i for i in occurrence if occurrence[i] == 1])

# Printing the set difference
print(f"Set difference: {set_diff}")

At the end of the program, we filtered out the element with frequency = 1 and converted it into a set. And finally printed the result in the console.

Method 2 - Using Set Operations 'Union' and 'Intersection'

Let us understand the idea first. Below is the Venn diagram of four sets.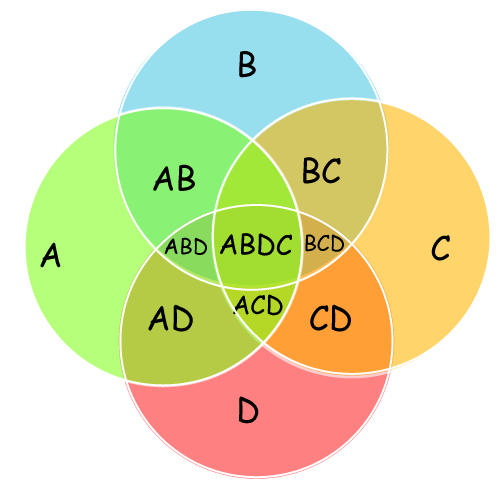

Symmetric Difference of Multiple Sets in Python

The symmetric difference of these sets will contain only A, B, C, and D parts. To find this, we will take the union of all sets and subtract the intersection of (A and B), (B and C), (C and D), and (A and D).

Union (A, B, C, D) = {A, B, C, D, AB, BC, CD, AD, ABC, BCD, ACD, ABD, ABCD}

Intersection (A, B) = {AB, ABC, ABD, ABCD}

Intersection (B, C) = {BC, ABC, BCD, ABCD}

Intersection (C, D) = {CD, BCD, ACD, ABCD}

Intersection (A, D) = {AD, ACD, ABD, ABCD}

Symmetric Difference (A, B, C, D) = Union (A, B, C, D) - Intersection (A, B) -Intersection (B, C) - Intersection (C, D) - Intersection (A, D)

Symmetric Difference (A, B, C, D) = {A, B, C, D} # Desired Output

# Define sets
set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}
set3 = {5, 6, 7, 8, 9}
set4 = {6, 7, 8, 9, 10}

# Finding the union of sets
union_of_Sets = set1.union(set2, set3, set4)

# Finding the intersection of sets
intersect_1 = set1.intersection(set2)
intersect_2 = set2.intersection(set3)
intersect_3 = set3.intersection(set4)
intersect_4 = set1.intersection(set4)

# Finding the set difference
set_diff = union_of_Sets - intersect_1 - intersect_2 - intersect_3

# Printing the set difference
print(f"Set difference: {set_diff}")

Output:

Set difference: {10, 1, 2, 3}

This method uses union and intersection to find the required unions and intersections. The problem with this method is that you have to calculate the intersection of sets separately, which can be avoided. There are some potential improvements in the program you can make, such as:

Using the *args syntax with set.union(): Instead of chaining the sets together using set1.union(set2, set3, set4), you can use the *args syntax with set.union(*sets) to unpack the sets into the union() method, which can make the code more concise.

Method 3 - Using XOR (^) Operator and Set Comprehension

In this method, we will use the XOR (^) operator to find the symmetric difference between sets and filter out all the elements that are present in exactly one set.

# Define sets
set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}
set3 = {5, 6, 7, 8, 9}
set4 = {6, 7, 8, 9, 10}

# Combine all sets into a list
sets = [set1, set2, set3, set4]

# Creating an empty set
symmetric_difference = set()

# Finding the symmetric difference using XOR (^) operator
for s in sets:
    symmetric_difference ^= s

# Finding the elements that are present only once in the symmetric difference
set_diff = {x for x in symmetric_difference if sum(x in s for s in sets) == 1}

# Printing the symmetric difference
print(f"Symmetric Difference: {set_diff}")

Output:

Symmetric Difference: {10, 1, 2, 3}

Explanation:

In the above code, the symmetric_difference variable stores {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. After finding the symmetric difference, we filtered out the elements that are present in exactly one set using the set comprehension method.

# Finding the elements that are present only once in the symmetric difference
set_diff = {x for x in set_union if sum(x in s for s in sets) == 1}

The sum(x in s for s in sets) == 1 condition, which counts the number of times an element appears in all sets and checks if it equal to 1. The filtered elements are stored in set_diff variable. And finally, the resulting symmetric difference is printed using print() statement with a formatted string.

Method 4 - Using Union Operator and Set Comprehension

In this method, we will first find the unique elements in all sets using the union operator. Then we will filter out the elements that are present in exactly one set using set comprehension.

# Define sets
set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}
set3 = {5, 6, 7, 8, 9}
set4 = {6, 7, 8, 9, 10}

# Combine all sets into a list
sets = [set1, set2, set3, set4]

# Finding the unique elements using the union operator
unique_elements = set().union(*sets)

# Finding the elements that are present only once in the symmetric difference
set_diff = {x for x in unique_elements if sum(x in s for s in sets) == 1}

# Printing the symmetric difference
print(f"Symmetric Difference: {set_diff}")

Output:

Symmetric Difference: {10, 1, 2, 3}

Explanation:

This method uses the union operator to find the unique elements and then filters out the elements that are present in exactly one set. For further understanding, see the explanation in method 3.

Method 5 - Using reduce function from functools

In this method, we will use the reduce function to find the symmetric difference and filter out the elements that are present in exactly one set using set comprehension as above.

# Importing the reduce function from functools
from functools import reduce

# Define sets
set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}
set3 = {5, 6, 7, 8, 9}
set4 = {6, 7, 8, 9, 10}

# Combine all sets into a list
sets = [set1, set2, set3, set4]

# Finding the unique elements using union operator
sym_diff = reduce(lambda x, y : x.symmetric_difference(y), sets)

# Finding the elements that are present only once in the symmetric difference
set_diff = {x for x in sym_diff if sum(x in s for s in sets) == 1}

# Printing the symmetric difference
print(f"Symmetric Difference: {set_diff}")

Output:

Symmetric Difference: {10, 1, 2, 3}

Explanation:

The reduce() function is used in combination with the lambda function to repeatedly apply the symmetric_difference() method on pairs of sets from the sets list, starting from the first set (set1) to the last set (set4).

A set comprehension filters the elements, and the filtered elements are stored in set_diff, representing the symmetric difference.

Next TopicPython Program to Find Duplicate Sets in a List of Sets

← prev next →