Implementation of Kruskal's Algorithm in Python

A weighted undirected graph's minimum spanning tree can be found using Kruskal's approach. Among all possible spanning trees, a minimum spanning tree is one that spans every vertex on the graph and has the lowest overall weight.

The algorithm works by sorting all the edges of the graph in increasing order of their weights and then adding the edges to the minimum spanning tree one by one if adding the edge does not create a cycle. It is done until all the vertices are connected.

Steps for Kruskal's algorithm

Here are the steps for Kruskal's algorithm:

Sort all the edges of the graph in increasing order of their weights.
Create a new empty set to represent the minimum spanning tree.
Iterate through each edge in the sorted list of edges.
Check whether adding the edge to the minimum spanning tree would create a cycle. Add the edge to the minimum spanning tree if it doesn't. Repeat until every vertex is joined.

Kruskal's algorithm has a time complexity of O(E log E), where E is the number of edges in the graph. It makes it a very efficient algorithm for finding the minimum spanning tree of large graphs.

Implementation of Kruskal's algorithm in python

The step-by-step implementation can be described as follows:

We define a Graph class with three instance variables: vertices, which is a list of all the vertices in the graph; edges, which is a list of all the edges in the graph; and adjacency_list, which is a dictionary representing the adjacency list of the graph.
We define a method add_edge to add an edge to the graph. This method takes three arguments: u and v, which are the vertices that the edge connects; and weight, which is the weight of the edge. We add the edge to the edges list and also add it to the adjacency_list.
We define a method find_parent to find the parent of a given vertex i in the disjoint-set data structure. The connected elements of the graph are tracked using the disjoint-set data structure. Each vertex is initially its own parent, and we use the find_parent method to find the root of the connected component that belongs to i.
We define a method union to merge two connected components in the disjoint-set data structure. The union method takes four arguments: parent, which is a dictionary representing the parent of each vertex; rank, which is a dictionary representing the rank of each vertex; x and y, which are the vertices whose connected components we want to merge. We use the find_parent method to find the roots of the connected components that belong to x and y, and then merge the components based on their rank.
We define a Kruskal method to implement Kruskal's algorithm. The method initializes an empty set minimum_spanning_tree to store the edges in the minimum spanning tree. It also initializes a parent dictionary and a rank dictionary for the disjoint-set.

Code:

class Graph:
    def __init__(self, vertices):
        self.vertices = vertices
        self.edges = []
        self.adjacency_list = {v: [] for v in vertices}

    def add_edge(self, u, v, weight):
        self.edges.append((u, v, weight))
        self.adjacency_list[u].append((v, weight))
        self.adjacency_list[v].append((u, weight))

    def find_parent(self, parent, i):
        if parent[i] == i:
            return i
        return self.find_parent(parent, parent[i])

    def union(self, parent, rank, x, y):
        root_x = self.find_parent(parent, x)
        root_y = self.find_parent(parent, y)
        if rank[root_x] < rank[root_y]:
            parent[root_x] = root_y
        elif rank[root_x] > rank[root_y]:
            parent[root_y] = root_x
        else:
            parent[root_y] = root_x
            rank[root_x] += 1

    def kruskal(self):
        minimum_spanning_tree = set()
        parent = {}
        rank = {}
        for v in self.vertices:
            parent[v] = v
            rank[v] = 0
        sorted_edges = sorted(self.edges, key=lambda x: x[2])
        for edge in sorted_edges:
            u, v, weight = edge
            root_u = self.find_parent(parent, u)
            root_v = self.find_parent(parent, v)
            if root_u != root_v:
                minimum_spanning_tree.add(edge)
                self.union(parent, rank, root_u, root_v)
        return minimum_spanning_tree
vertices = [0, 1, 2, 3]
g = Graph(vertices)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 10)
g.add_edge(0, 3, 3)
g.add_edge(1, 3, 1)
g.add_edge(2, 3, 4)
minimum_spanning_tree = g.kruskal()
print(minimum_spanning_tree)

Output:

{(1, 3, 1), (2, 3, 4), (0, 3, 3)}

The input graph is as below:

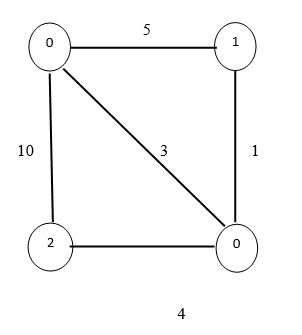
Implementation of Kruskal's Algorithm in Python

Kruskal's algorithm is a greedy algorithm for finding the minimum spanning tree of a connected, weighted graph.

This set represents the edges in the minimum spanning tree of the input graph. We can see that the total weight of the minimum spanning tree is 1 + 3 + 5 = 9.

The algorithm works by sorting the edges of the graph by weight and then adding the edges to the minimum spanning tree one by one, starting with the smallest weight.
As each edge is added to the minimum spanning tree, it is checked to ensure that it does not create a cycle. If the edge connects two vertices that are already in the same connected component, then adding the edge would create a cycle, and the edge is discarded.
As long as the graph is connected and the edge weights are distinct, Kruskal's approach will always identify the graph's minimum spanning tree.
The time complexity of Kruskal's algorithm is O(E log E), where E is the number of edges in the graph. It is because the algorithm requires sorting the edges by weight, which takes O(E log E) time, and then processing each edge one by one, which takes O(E)
The space complexity of Kruskal's algorithm is O(V + E), where V is the number of vertices in the graph and E is the number of edges. It is because the algorithm requires storing the edges and the adjacency list of the graph, as well as the disjoint-set data structure used to keep track of the connected components.
Kruskal's algorithm can be implemented using a priority queue to sort the edges by weight more efficiently. It improves the algorithm's time complexity to O(E log V), where V is the graph's vertex However, the space complexity remains O(V + E).
In some cases, there may be multiple minimum spanning trees for a given graph. Kruskal's algorithm will find one of these trees, but not necessarily all of them.

Kruskal's algorithm is often used in network design problems, such as designing a communication network or an electrical power grid. The algorithm can also be implemented using a priority queue in python:

Code:

import queue
class Graph:
    def __init__(self, vertices):
        self.vertices = vertices
        self.edges = []
        self.parent = {}
        self.rank = {}

        for v in self.vertices:
            self.make_set(v)

    def add_edge(self, u, v, w):
        self.edges.append((w, u, v))

    def make_set(self, v):
        self.parent[v] = v
        self.rank[v] = 0

    def find(self, v):
        if self.parent[v] != v:
            self.parent[v] = self.find(self.parent[v])
        return self.parent[v]

    def union(self, u, v):
        root1 = self.find(u)
        root2 = self.find(v)

        if root1 != root2:
            if self.rank[root1] > self.rank[root2]:
                self.parent[root2] = root1
            else:
                self.parent[root1] = root2
                if self.rank[root1] == self.rank[root2]:
                    self.rank[root2] += 1

    def kruskal(self):
        minimum_spanning_tree = set()

        # Sort edges by weight using priority queue
        edge_queue = queue.PriorityQueue()
        for edge in self.edges:
            edge_queue.put(edge)

        # Iterate through edges in priority queue and add to MST
        while not edge_queue.empty():
            weight, u, v = edge_queue.get()

            if self.find(u) != self.find(v):
                self.union(u, v)
                minimum_spanning_tree.add((u, v, weight))

        return minimum_spanning_tree
# Create a graph with 5 vertices
g = Graph([0, 1, 2, 3, 4])

# Add edges to the graph
g.add_edge(0, 1, 2)
g.add_edge(0, 2, 3)
g.add_edge(0, 3, 6)
g.add_edge(1, 2, 5)
g.add_edge(1, 4, 3)
g.add_edge(2, 3, 1)
g.add_edge(2, 4, 4)
g.add_edge(3, 4, 5)

# Find the minimum spanning tree
mst = g.kruskal()

# Print the edges in the minimum spanning tree
for edge in mst:
    print(edge)

Output:

(2, 3, 1)
(0, 2, 3)
(0, 1, 2)
(1, 4, 3)

These are the edges in the minimum spanning tree for the same above graph.

In this implementation, we use a priority queue to sort the edges by weight. We add each edge to the priority queue with its weight as the priority, so that when we retrieve edges from the queue, we always get the edge with the smallest weight first. After that, we iterate through the edges in the priority queue and add them to the minimum spanning tree one by one, as long as they don't create a cycle. We keep track of the connected components of the graph using the find and union methods of the disjoint-set data structure, just like in the previous implementation.

To use this implementation, you would create a Graph object, add edges to it using the add_edge method, and then call the kruskal method to find the minimum spanning tree.

Next TopicMocking External API in Python

← prev next →