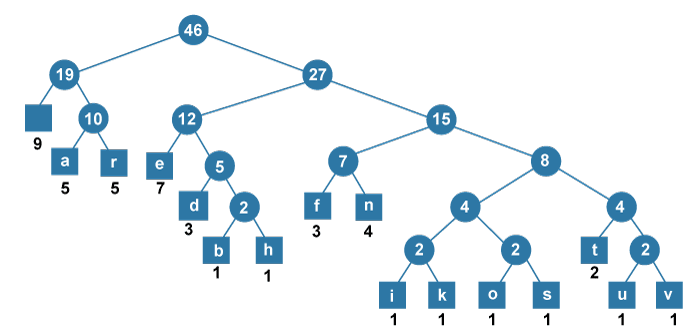
Huffman Coding using PythonHuffman coding is a lossless method for compressing and encoding text based on the frequency of the characters in the text. In information theory and computer science studies, Huffman code is a special type of optimal prefix code that is generally utilized for lossless data compression. In the following tutorial, we will be going to understand the theory of Huffman Coding along with its implementation using the Python programming language. But we get to that; let us understand the Huffman Coding in brief. Understanding the Huffman CodingHuffman Coding is a Lossless Compression Algorithm that is utilized for data compression. It is an algorithm developed by David A. Huffman while he was an Sc.D. Student at Massachusetts Institute of Technology (MIT) published in the year 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". It was a part of his research into Computer Programming and is generally found in programming languages like C, C++, Python, Java, JavaScript, Ruby, and many more. The thought process behind Huffman encoding is as follows: A letter or a symbol that occurs often is exemplified using a shorter code, and a letter or symbol that occurs infrequently is exemplified using a longer code. This thought leads to an efficient depiction of characters that need less memory to be stored. Hence, we can conclude that we can use Huffman coding as a data compression method. Let us now understand the theory of Huffman coding. Understanding the Theory of Huffman CodingWe know that a file is stored on a computer as binary code and that each character in the file has been assigned a binary character, and the character codes generally have a fixed length for distinct characters. Huffman coding is established on the frequency with which each character in the file appears and the number of characters in a data structure with a frequency of zero (0). The Huffman encoding for a typical text file saves around 40 percent of the size of the actual data. Huffman binary code, like compiled executables, would thus have a distinct space-saving. A binary file in which an ASCII character is encoded with a frequency of 0.5 would have a very different frequency and distribution from its ASCII equivalent. In order to compress a file using a sequence of characters, we require a table that provides us with the sequences of bits utilized for each character. This table generates an encoding tree that utilizes the root/leaf path in order to create a bit sequence that encodes the characters. We can follow the roots and leaves to create a list of characters with the maximum bit length of the encoded characters and the number of occurrences. We can use a greedy algorithm in order to construct an optimal tree. Huffman encoding trees return the minimum length character encodings utilized in compressing the data. The nodes in the tree depict the frequency of the occurrence of the character. The root node depicts the length of the string, and traversing the tree provides us with the encodings specified to the character. Once the tree is constructed, traversing the tree provides us with the respective codes of each symbol. The optimal tree upon completion is shown in the following table and image:
Let us now develop and implement a program that utilizes Huffman coding in the following section. Huffman Code Implementation using PythonWe will start by creating a class as Nodes, referred to as the nodes of the Binary Huffman Tree. Essentially, each node consists of a symbol and associated probability variable, left and right child, and code variable. Code variable will either be 0 or 1 depending on the side we choose (left for 0 and right for 1) while traveling through the Huffman Tree. Let us consider the following snippet of code demonstrating the same: Example: Explanation: In the above snippet of code, we have defined a class as Nodes and initialized some parameters as probability, symbol, left, and right. We have initially set the values of the left and right variables as None as the direction is not defined yet. At last, we have also initialized the code variable. Now, we will add some supporting functions. The first function is to calculate the probabilities of the symbols in the provided data. The second function is to obtain encodings of symbols that we will use once we have the Huffman Tree. The last function is to obtain the result (encoded data). Example: Explanation: In the above snippet of code, we have defined three different helper functions in order to calculate probabilities of the symbols in the given data, obtain the encoding of symbols, and obtain the result. For the first function, we have defined a dictionary as the_symbols and iterate through the items in the given data using the for-loop and insert them into the dictionary. We have also used the if-else conditional statement to check if the data contains some element or not and perform the operation accordingly. For the second function, we have defined another dictionary as the_codes. Within the function, we have assigned a variable storing the Huffman code for the current node and used the if conditional statements to add the nodes at the left and right with the current node and return the symbols encoding. For the last function, we have created an empty array. We have then used the for-loop iterating through the characters in the data and append() function to add data to the array. We have then used the join() function to join the elements from the array to the string and returned the string. Moreover, we will also define another function as TotalGain, which accepts the initial data and the dictionary coming from CalculateCode, holding the symbols and their codes together. That function will help us calculate the difference between the size of a bit of compressed and non-compressed data. Let us consider the following snippet of code demonstrating the same: Example: Explanation: In the above snippet of code, we have defined the function. We calculated the total bit space to store the data before compression. We have then defined a variable to store the bit space size after data compression and assigned it to zero. We have then iterated through the keys from the dictionary from the CalculateCode function and counted their occurrences. We have then calculated the bit space that requires to store the data after compression. We will use the HuffmanEncoding function, which accepts only the data as an argument and returns the resulting encoding and the total gain using all the above-described functions. Let us understand the same using the following snippet of code: Example: Explanation: In the above snippet of code, we used the data argument, calculated the probability of symbols using the CalculateProbability function, and stored the resulting data in a variable. We have then extracted the symbols (keys) and probabilities (values) and printed them for the users. We have then defined an array as the_nodes and converted the symbols and probabilities into the nodes of the Huffman tree. We have used the for-loop iterating through the symbols and appending them to the array. We have also used the while loop in order to sort the nodes in ascending order based on their probabilities. We selected the two smallest nodes and combined them to create a new node. We removed the smallest nodes from the array and added the new node to it. We have then used the CalculateCodes function to calculate the code for the Huffman encoding and print the symbols with codes for the users. We have also used the TotalGain function, providing the required parameters to calculate the difference between the bit space of compressed and non-compressed data. At last, we have printed the result and returned the encodedOutput and the zeroth index of the array. Now, we will define a function in order to decode Huffman Encoded data for obtaining the initial, uncompressed data again which is quite a simple process. Let us consider the following snippet of code demonstrating the process of decoding Huffman Encoded data. Example: Explanation: In the above snippet of code, we have defined a function as HuffmanDecoding that accepts two parameters as encodedData and huffmanTree. We have then assigned the huffmanTree variable to another variable. We have also defined an empty array as decodedOutput. We have then used the for-loop to iterate through the elements in the encoded data. Within the loop, we have used the if-elif-else conditional statement and try-exception method in order to decode the encoded data and append each decoded element to generate a decoded output. At last, we have created a string and returned the string for the users. Now, let us initialize the string data and print the results. Example: Explanation: In the above snippet of code, we have defined string data and printed it for the users. We passed this data to the HuffmanEncoding function and stored the values in encoding and the_tree variables. We have then printed the Encoded result for the users. At last, we have passed the encoded data to the HuffmanDecoding function and printed the decoded string. Let us now see the complete project before its execution. The Complete Project Code Let us see the complete Python project code of the Huffman coding. File: huffmanAlgo.py Output:
AAAAAAABBCCCCCCDDDEEEEEEEEE
symbols: dict_keys(['A', 'B', 'C', 'D', 'E'])
probabilities: dict_values([7, 2, 6, 3, 9])
symbols with codes {'E': '00', 'A': '01', 'C': '10', 'D': '110', 'B': '111'}
Space usage before compression (in bits): 216
Space usage after compression (in bits): 59
Encoded output 01010101010101111111101010101010110110110000000000000000000
Decoded Output AAAAAAABBCCCCCCDDDEEEEEEEEE
Next TopicNested Dictionary in Python
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










