Box-Cox Transformation in Python

In our environment, data is distributed randomly, where some data refers to the peak value of the curve of the dataset, whereas some data points refer to the tail part of the curve. For any dataset, we can calculate the distribution using its variance and mean, and we can see how far the data is distributed to the mean value.

Generally, we can divide the distribution of the data into two ways:

Normal distribution
Non-normal or Power-law distribution

Normal distribution

In this type of distribution, the distribution of the data along the mean value is very consistent. Here, we get the peak value of the curve throughout the mean value, and data is distributed symmetrically along the mean value.

We can easily implement analysis techniques on the normally distributed data.

Power-law distribution

In this type of distribution, we will be having the peak of the curve for some small datasets, and then we will be having a long tail for the curve for a large number of datasets.

But in the environment, the nature of data is not always normally distributed. So with the help of box-cox transformation, we can transform the power-law distributed data into the normally distributed data using some mathematical formula.

The mathematical analysis for transformation is that we will find the value of such that the non-normally distributed transforms are as close as possible to the normally-distributed dataset.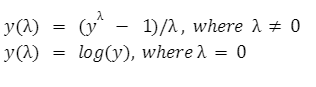

To implement box-cox transformation, we will use the scipy library, and the function will be the scipy.stats.boxcox() function.

Syntax:

InputArray

This is the dataset which we want to transform into a normal-distributed dataset.

Lamda

If the lambda is none, we will find out the value of lambda that maximizes the value log function, and if it is not none then on the value of lambda, we perform the transformation.

Alpha

This is an optional parameter which takes a float value between 0.0 to 1.0. If the lambda is none, then it is taken under consideration, and if lambda is not none, it is ignored.

Optimizer

It is an optional and callable parameter which is called when it is needed. When the value of lambda is none, then this optimizer is used to find the value of lambda that minimizes the log function.

Example:

In this example, we will take the dataset of non-normal distribution, and then we will transform it into the normally-distributed dataset.

#python 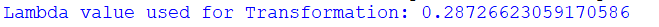code to transform non-normal data into normal-distributed data
# importing the required modules
import numpy as np
from scipy import stats

# importing the plotting modules
import seaborn as sns
import matplotlib.pyplot as plt

# generating the random non-normal data (exponential)
originalData = np.random.exponential(size = 1200)

# transforming the data into normal data and getting the lambda value
fittedData, lambdaValue = stats.boxcox(originalData)

# creating the axes to draw plots of datasets
fig, ax = plt.subplots(1, 2)

#plotting the non-normal or original data using histplot() function
sns.histplot(originalData, kde = True,stat="density",linewidth=2,label = "Non-Normal distribution", color ="red", ax = ax[0])

#plotting the normal or original data using the histplot() function
sns.histplot(fittedData, kde = True,stat="density",linewidth=2,label = "Normal distribution", color ="blue", ax = ax[1])

# adding legends to the subplots
plt.legend(loc = "upper right")
# rescaling the subplots
fig.set_figheight(5)
fig.set_figwidth(10)
print(f"Lambda value used for Transformation: {lambdaValue}")
#displaying the plots
plt.show()

Output:

Explanation:

In the above code, first, we have imported the required modules in the file like numpy,scipy, matplotlib and seaborn to plot the curve. Now with the help of the random function of numpy, we created the random dataset of 1200 data points. Now we use the boxcox() function, which takes the dataset as an argument and returns the transformed dataset and lambda value.

Now using the histplot() function, we plotted the curve of the original dataset and transformed the dataset. The histplot() function takes a dataset as an argument, and it has many more attributes like color, linewidth etc., which define the specification of the curve. Now with the show() function, we have displayed the curve before the transformation and after the boxcox transformation.

For the above random dataset, we got the lambda value as 0.2872, which is nearly equal to 0.28.

So in the dataset, the new values will be according to this formula:

New Value = (Old Value0.2872 -1)/0.2872

Next TopicAssertionError in Python

← prev next →