Implementation of Linear Regression using Python

Linear regression is a statistical technique to describe relationships between dependent variables with a number of independent variables. This tutorial will discuss the basic concepts of linear regression as well as its application within Python.

In order to give an understanding of the basics of the concept of linear regression, we begin with the most basic form of linear regression, i.e., "Simple linear regression".

Simple Linear Regression

Simple linear regression (SLR) is a method to predict a response using one feature. It is believed that both variables are linearly linked. Thus, we strive to find a linear equation that can predict an answer value(y) as precisely as possible in relation to features or the independently derived variable(x).

Let's consider a dataset in which we have a number of responses y per feature x:

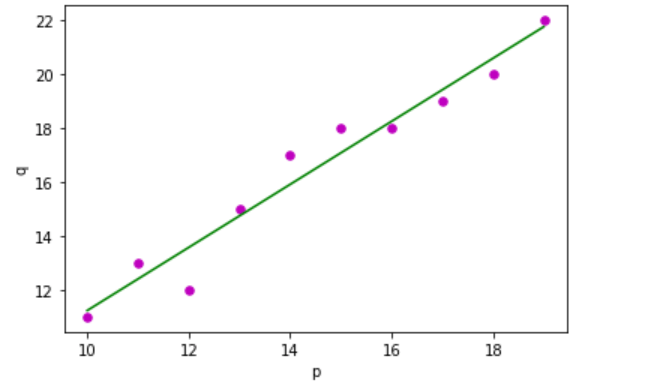
Implementation of Linear Regression using Python

For simplification, we define:

x as feature vector, i.e., x = [x₁, x₂, x₃, …., x_n],

y as response vector, i.e., y = [y₁, y₂, y₃ …., y_n]

for n observations (in above example, n = 10).

A scatter plot of the above dataset looks like: -

The next step is to identify the line that is most suitable for this scatter graph so that we can anticipate the response of any new value for a feature. (i.e., the value of x is that is not in the dataset)

This line is referred to as the regression line.

The equation of the regression line can be shown as follows: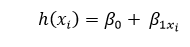

Here,

h(x_i ) signifies the predicted response value for i^th
?₀ and ?_{1x_i} ) are regression coefficients and represent y-intercept and slope of regression line respectively.

In order to build our model, we need to "learn" or estimate the value of the regression coefficients and . After we've determined those coefficients, then we are able to make use of this model in order to forecast the response!

In this tutorial, we're going to employ the concept of Least Squares.

Let's consider:

y_i = ?₀+ ?_{1x_i} + ?_i=h(x_i )+ ?_i ? ?_i= y_i- h(x_i )

Here, ?_i is a residual error in i^th observation.

So, our goal is to minimize the total residual error.

We have defined the cost function or squared error, J as: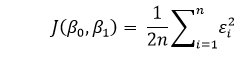

and our mission is to find the value of ?₀ and ?₁ for which J(?₀,?₁) is minimum.

Without going into the mathematical details, we are presenting the result below: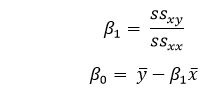

Where, ss_xy would be the sum of the cross deviations of "y" and "x":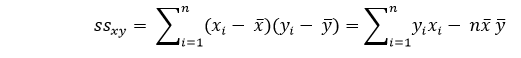

And ss_xx would be the sum of squared deviations of "x"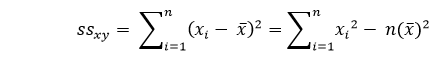

Code:

import numpy as nmp
import matplotlib.pyplot as mtplt

def estimate_coeff(p, q):
# Here, we will estimate the total number of points or observation
	n1 = nmp.size(p)
# Now, we will calculate the mean of a and b vector
	m_p = nmp.mean(p)
	m_q = nmp.mean(q)

# here, we will calculate the cross deviation and deviation about a
	SS_pq = nmp.sum(q * p) - n1 * m_q * m_p
	SS_pp = nmp.sum(p * p) - n1 * m_p * m_p

# here, we will calculate the regression coefficients
	b_1 = SS_pq / SS_pp
	b_0 = m_q - b_1 * m_p

	return (b_0, b_1)

def plot_regression_line(p, q, b):
# Now, we will plot the actual points or observation as scatter plot
	mtplt.scatter(p, q, color = "m",
			marker = "o", s = 30)

# here, we will calculate the predicted response vector
	q_pred = b[0] + b[1] * p

# here, we will plot the regression line
	mtplt.plot(p, q_pred, color = "g")

# here, we will put the labels
	mtplt.xlabel('p')
	mtplt.ylabel('q')

# here, we will define the function to show plot
	mtplt.show()

def main():
# entering the observation points or data
	p = np.array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
	q = np.array([11, 13, 12, 15, 17, 18, 18, 19, 20, 22])

# now, we will estimate the coefficients
	b = estimate_coeff(p, q)
	print("Estimated coefficients are :\nb_0 = {} \
		\nb_1 = {}".format(b[0], b[1]))

# Now, we will plot the regression line
	plot_regression_line(p, q, b)

if __name__ == "__main__":
	main()

Output:

Estimated coefficients are :
b_0 = -0.4606060606060609 		
b_1 = 1.1696969696969697

Multiple linear regression

Multiple linear regression attempts explain how the relationships are among several elements and then respond by applying a linear equation with the data. Clearly, it's not anything more than an extension of linear regression.

Imagine a set of data that has one or more features (or independent variables) as well as one response (or dependent variable).

The dataset also is comprised of additional n rows/observations.

We define:

X(Feature Matrix) = it is a matrix of size "n * p" where "x_ij" represents the values of j^th attribute for the i^th observation.

Therefore,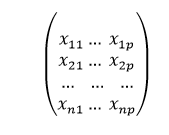

And,

y (Response Vector) = It is a vector of size n where represents the value of response for the i^th observation.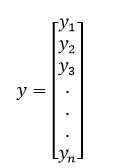

The regression line for "p" features are represented as: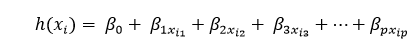

Where h(x_i) is the predicted response value for the i^th observation point and ?₀,?₁,?₂,....,?_p are the regression coefficients.

We can also write: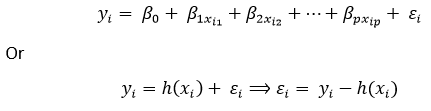

Where, ?_i is representing the residual error in the ith observation point.

We can also generalize our linear model a little more by representing the attribute matrix of "X" as: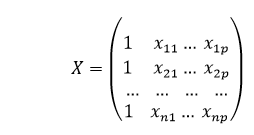

Therefore, the linear model can be expressed in the terms of matrices as shown below:

y=X?+?

Where,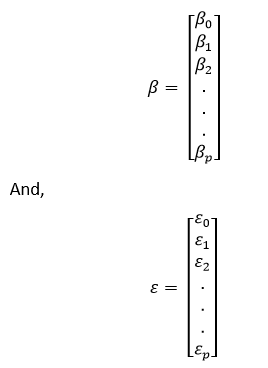

We now determine an estimation of the b, i.e., b' by with an algorithm called the Least Squares method. As previously mentioned, this Least Squares method is used to find b' for the case where the residual error of total is minimized.

We will present the results as shown below: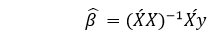

Where ' is the matrix's transpose and -1 is the matrix's that is the reverse.

With the help of the lowest square estimates b', the multi-linear regression model is now calculated by: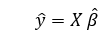

where y' is the estimated response vector.

Code:

import matplotlib.pyplot as mtpplt
import numpy as nmp
from sklearn import datasets as DS
from sklearn import linear_model as LM
from sklearn import metrics as mts

# First, we will load the boston dataset
boston1 = DS.load_boston(return_X_y = False)

# Here, we will define the feature matrix(H) and response vector(f)
H = boston1.data
f = boston1.target

# Now, we will split X and y datasets into training and testing sets
from sklearn.model_selection import train_test_split as tts
H_train, H_test, f_train, f_test = tts(H, f, test_size = 0.4,
													random_state = 1)

# Here, we will create linear regression object
reg1 = LM.LinearRegression()

# Now, we will train the model by using the training sets
reg1.fit(H_train, f_train)

# here, we will print the regression coefficients
print('Regression Coefficients are: ', reg1.coef_)

# Here, we will print the variance score: 1 means perfect prediction
print('Variance score is: {}'.format(reg1.score(H_test, f_test)))

# Here, we will plot for residual error

# here, we will set the plot style
mtpplt.style.use('fivethirtyeight')

# here we will plot the residual errors in training data
mtpplt.scatter(reg1.predict(H_train), reg1.predict(H_train) - f_train,
			color = "green", s = 10, label = 'Train data')

# Here, we will plot the residual errors in test data
mtpplt.scatter(reg1.predict(H_test), reg1.predict(H_test) - f_test,
			color = "blue", s = 10, label = 'Test data')

# Here, we will plot the line for zero residual error
mtpplt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)

# here, we will plot the legend
mtpplt.legend(loc = 'upper right')

# now, we will plot the title
mtpplt.title("Residual errors")

# here, we will define the method call for showing the plot
mtpplt.show()

Output:

Regression Coefficients are:  [-8.95714048e-02  6.73132853e-02  5.04649248e-02  2.18579583e+00
 -1.72053975e+01  3.63606995e+00  2.05579939e-03 -1.36602886e+00
  2.89576718e-01 -1.22700072e-02 -8.34881849e-01  9.40360790e-03
 -5.04008320e-01]
Variance score is: 0.7209056672661751

In the above example, we calculate the accuracy score using the Explained Variance Score.

We define:

explained_variance_score = 1 - Var{y - y'}/Var{y}

where y' is the estimated output target, where y is the equivalent (correct) to the target's output, where Var is Variance, which is the square of the standard deviation.

The most ideal score is 1.0. Lower scores are worse.

Assumptions:

Here are the main assumptions that the linear regression model is based on with regard to the dataset on the basis on which it is utilized:

Linear relationships: Relationship between feature and response variables must be linear. The assumption of linearity is tested with the help of scatter plots. As we can see, the 1st figure is a representation of linearly related variables, whereas the variables in the 3rd and 2nd figures are probably non-linear. Thus, 1st figure can make more accurate predictions by using linear regression.
Little or no multi-collinearity: is the assumption that there is minimal or no multicollinearity present in the data. Multi-collinearity happens when the features (or independent variables) aren't independent of each other.
Little or no auto-correlation: Another theory could be that there's not much or no autocorrelation within the data. Autocorrelation is when residual errors aren't independent of one another.
Homoscedasticity: is refer to an instance where errors are a factor (that is, the "noise" or random disturbance in the relationship between independent variables and dependent variables) that remains the same for all independent variables. Figure 1 is homoscedastic, while figure 2 displays heteroscedasticity.

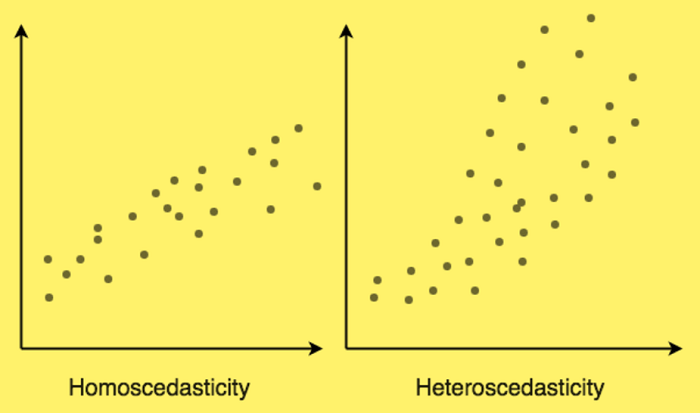
At the end of the tutorial, we'll discuss some of the applications of linear regression.

Applications:

Following are the fields of applications based on Linear Regression:

Trend lines: illustrate the changes in the quantity of data as the passing in time (like GDP or oil prices, for instance.). They typically have a linear connection. Therefore, linear regression could be used to predict future value. However, the method is not able to meet the requirements of scientific credibility in situations when other possible changes may alter the data.
Economics: Linear Regression is the primary tool used in economics. It can be employed to predict the amount of spending by consumers and fixed investment spending investments in inventory, purchases of exports of a country, spending on imports, demand to store liquid assets, demand for labour, and supply.
Financial: A model of capital value assets makes use of linear regression to study and quantify the risk factors of investing.
Biology: Linear regression is a method to explain causal relationships between variables in biological systems.

Next TopicNested Decorators in Python

← prev next →