Sklearn Logistic Regression

In this tutorial, we will learn about the logistic regression model, a linear model used as a classifier for the classification of the dependent features. We will implement this model on the datasets using the sklearn logistic regression class.

What is logistic regression?

Predictive analytics and classification frequently use this kind of machine learning regression model, also referred to as a logit model. Depending on the given dataset of independent features, the logistic regression model calculates the probability that an event will occur, such as voting or not voting. Given that the result is a probability of happening an event, the dependent feature's range is 0 to 1.

In the logistic regression model, the odds of winning the probability of success of an event divided by the probability of failure-are transformed using the logit formula. The following formulas are used to represent this logistic function, which is sometimes referred to as the log odds or the natural logarithm of odds: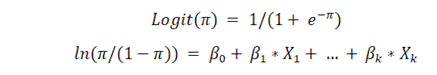

Logit(pi) is the dependent or target feature in the equation of the logistic regression model, while x is the independent feature. The most frequent method for estimating the coefficients in this linear model is by using the maximum likelihood estimation (MLE). To find the best fit for the log odds, this approach iteratively evaluates various values of the coefficients.

The log-likelihood function is created after each of these iterations, and logistic regression aims to maximise this function to get the most accurate parameter estimate. The conditional probabilities for every class of the observations can be computed, logged, and added together to produce a forecast probability once the best coefficient (or coefficients, if there are multiple independent features) has been identified.

If the classification is binary, a probability of less than 0.5 predicts 0, and a probability of more than 0 indicates 1. Once the logistic regression model has been computed, it is recommended to assess the linear model's goodness of fit or how well it predicts the classes of the dependent feature. The Hosmer-Lemeshow test is a well-liked technique for evaluating model fit.

Sklearn Logistic Regression Example

Sklearn Logistic Regression

class sklearn.linear_model.LogisticRegression(penalty = 'l2', *, dual = False, tol = 0.0001, C = 1.0, fit_intercept = True, intercept_scaling = 1, class_weight = None, random_state = None, solver = 'lbfgs', max_iter = 100, multi_class = 'auto', verbose = 0, warm_start = False, n_jobs = None, l1_ratio = None)

Parameters:

penalty{'l1', 'l2', 'elasticnet', 'none'}, default='l2': This parameter will define the rule for the penalty:
"none": No penalty is imposed;
"l2": if you specify an L2 penalty term, it is the default option.
Specify an L1 penalty term with the "l1" command.
Specify an L1 and L2 penalty term with the 'elasticnet' command.
dualbool, default=False: This parameter defines the type of formulation, dual or primary.
tolfloat, default=1e-4: This specifies the tolerance value to stop the iteration.
Cfloat, default=1.0: It is the inverse of the regularisation strength and must be a positive floating point number.
fit_interceptbool, default=True: This parameter specifies if bias or intercept constant must be included in the decision function.
intercept_scalingfloat, default=1: It is useful only if self.fit_intercept is defined as True and the solver 'liblinear' is applied.
class_weightdict or 'balanced', default=None: This parameter associates weights to the classes in the format {"class label: weight"}. All classes are expected to possess weight one if weights are not provided.
random_stateint, RandomState instance, default=None: This parameter is used to shuffle the input data if the solver is ["sag," "saga," or "liblinear"].
solver{'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}, default='lbfgs ': Algorithm to use in the optimization problem. Default is 'lbfgs'.

Sklearn Logistic Regression Classifier

Code

# Python program to implement sklearn logistic regression model on load_iris dataset of sklearn

# Importing the required libraries
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

# Loading the dataset
X, Y = load_iris(return_X_y = True)

# Creating an instance of the class Logistic Regression model
logreg = LogisticRegression(random_state = 0)

# Fitting the dataset to the logistic regression model
logreg.fit(X, Y)

# Predicting the values
Y_pred = logreg.predict(X[:2, :])
print(Y_pred)
Y_predict = logreg.predict_proba(X[:2, :])
print(Y_predict)

# Calculating the accuracy score of the model
score = logreg.score(X, Y)
print(score)

Output:

[0 0]
[[9.81764058e-01 1.82359281e-02 1.43020498e-08]
 [9.71660947e-01 2.83390229e-02 2.99214023e-08]]
0.9733333333333334

Logistic Regression CV Example

Code

# Python program to implement sklearn logistic regression CV model on load_iris dataset of sklearn

# Importing the required libraries
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegressionCV

# Loading the dataset
X, Y = load_iris(return_X_y = True)

# Creating an instance of the class Logistic Regression CV
logreg = LogisticRegressionCV(cv = 4, random_state = 0)

# Fitting the dataset to the logistic regression CV model
logreg.fit(X, Y)

# Predicting the values
Y_pred = logreg.predict(X[:2, :])
print(Y_pred)
Y_predict = logreg.predict_proba(X[:2, :])
print(Y_predict)

# Calculating the accuracy score of the model
score = logreg.score(X, Y)
print(score)

Output:

[0 0]
[[9.91624054e-01 8.37594552e-03 2.92559111e-11]
 [9.85295789e-01 1.47042107e-02 1.03510087e-10]]
0.9866666666666667

Scikit-learn Logistic Regression Coefficients

In this part, we will learn how to use the sklearn logistic regression coefficients.

A number to which we multiply the value of an independent feature is referred to as the coefficient of that feature. Here, a feature's size and direction are expressed using logistic regression.

Code

# Python code to see how to perform Logistic Regression using sklearn.linear_model

# Importing the required modules and classes
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# Loading our dataset
data = load_iris()

# Splitting the independent and dependent variables
X = data.data
Y = data.target
print("The size of the complete dataset is: ", len(X))

# Creating an instance of the LogisticRegression class for implementing logistic regression 
log_reg = LogisticRegression()

# Segregating the training and testing dataset
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state = 10)

# Performing the logistic regression on train dataset
log_reg.fit(X_train, Y_train)

# Printing the coefficients
print(log_reg.coef_)

Output:

The size of the complete dataset is:  150
[[-0.35041623  0.91723236 -2.23583834 -0.97778255]
 [ 0.56061567 -0.44283218 -0.21739708 -0.64651405]
 [-0.21019944 -0.47440019  2.45323542  1.6242966 ]]

Sklearn Logistic Regression Feature Importance

In this part, we will study sklearn's logistic regression's feature importance.

A method called "feature importance" assigns a weight to each independent feature and, based on that value, concludes how valuable the information is in forecasting the target feature.

Code

# Python program to learn feature importance for logistic regression

# Importing the required libraries
from sklearn.datasets import make_classification 
from sklearn.linear_model import LogisticRegression 
import matplotlib.pyplot as plt

# Creating dependent and independent features using make_classification of sklearn
X, y = make_classification(n_samples = 1500, n_features = 5, n_informative = 3, n_redundant = 2, random_state = 10) 

# Creating an instance of the model
logreg = LogisticRegression()

# Fitting our data to train the model
logreg.fit(X, y)

weights = logreg.coef_[0]
print(weights)

# Plotting feature importance graph for each feature
for ind, coeff in enumerate(weights): 
    print(f"Feature: {ind}, weight: {coeff}") 
    
plt.bar([n for n in range(len(weights))], weights) 
plt.show()

Output:

[ 1.96365376 -0.11875128 -0.32930302  1.23664458 -1.40461804]
Feature: 0, weight: 1.9636537611525497
Feature: 1, weight: -0.1187512810730595
Feature: 2, weight: -0.32930302369908127
Feature: 3, weight: 1.236644582783369
Feature: 4, weight: -1.4046180417231233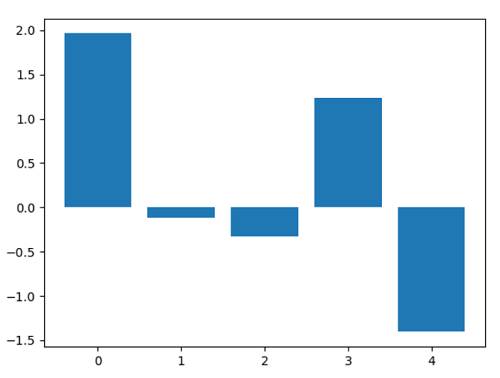

Sklearn Logistic Regression Cross-Validation

Code

# Python program to test the accuracy of the Logistic Regression model using a cross-validation test

# Improting the required libraries
from numpy import mean, std
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score, KFold

# Creating dependent and independent features using make_classification of sklearn
X, y = make_classification(n_samples = 1500, n_features = 25, n_informative = 20, n_redundant = 5, random_state = 10) 

# Creating an instance of the model
logreg = LogisticRegression()

# Fitting our data to train the model
logreg.fit(X, y)

# Using KFold cross-validation to validate the dataset
cross_validation = KFold(n_splits = 10, random_state = 1, shuffle = True) 

# Calculation score using cross_val_score
score = cross_val_score(logreg, X, y, scoring = 'accuracy', cv = cross_validation, n_jobs = -1) 
print("Cross-validation accuracy scores of each split is: ", score)
print("mean and standard deviation of the scores is: ", mean(score), std(score))

Output:

Cross-validation accuracy scores of each split is: [0.80666667 0.80666667 0.81333333 0.86666667 0.78666667 0.8
 0.78       0.82       0.80666667 0.83333333]
mean and standard deviation of the scores is:  0.812 0.023247461032216934

Next TopicWhat is Sklearn in Python

← prev next →