Sklearn Ensemble

Multiple machine learning algorithms are used in ensemble learning, aiming to improve the correct prediction ratio on a dataset. A dataset is used to train a list of machine learning models, and the distinct predictions made by each of the models applied to the dataset form the basis of an ensemble learning model. The ensemble model then combines the outcomes of different models' predictions to get the final result.

Each model has advantages and disadvantages. By integrating different independent models, ensemble models can effectively mask a particular model's flaws.

Typically, ensemble techniques fall into one of two categories:

Boosting

By transforming poor learning models into strong learners, the boosting machine learning ensemble model uses the approach to lower the bias and variance in the dataset. The dataset is sequentially introduced to poor machine-learning models. The first stage is to make a preliminary model and fit that model into the created training dataset.

Then, a secondary model that aims to correct the previous model's flaws is fitted. Here is the step-wise detail of the complete procedure:

• From the original dataset, construct a subset.
• Create a preliminary model using this sub-dataset.
• Make predictions through this preliminary model using the entire collection of the dataset.
• Utilize the predictions made by the model and the true values of those features to calculate the accuracy score.
• Give the wrong predictions a greater weight.
• Build a second model that is better than the previous one, which tries to correct the flaws in the previous model.
• Using this new and better model, make predictions by inputting the complete dataset.
• Make several different models; each one must be intended to fix the mistakes made by the one applied before it.

We can determine the final model by weighing the average of each model.

Examples: AdaBoost, Gradient Tree Boosting

Averaging

In averaging, the final output is an average of all predictions. This goes for regression problems. For example, in random forest regression, the final result is the average of the predictions from individual decision trees.

Let's take an example of three regression models that predict the price of a commodity as follows:

regressor 1 ? 200

regressor 2 ? 300

regressor 3 ? 400

The final prediction would be an average of 200, 300, and 400.

Examples: Bagging methods, Forests of randomized trees

Some Sklearn Ensemble Methods

AdaBoost

The result of averaging is a mean of all the predictions made by different. This is used for regression cases. The outcome, for instance, in random forest regression is the mean of the forecasts from many decision trees.

Let's look at an illustration of 3 regression models that forecast the cost of a good:

100 by Regressor 1

300 by regressor 2

400 by regressor 3

• The final result will be an average of these different predictions.
• The weights assigned to each observation of the dataset are initially the same.
• A subset of the entire data is used to construct a preliminary model.
• Predictions are generated using this preliminary model for the entire dataset.
• The accuracy score is computed by evaluating the predicted and true values of the observations.
• The data values this model inaccurately predicted are given greater weight when building the subsequent model.
• We may calculate weights based on the error value. For instance, the weight attributed to the observation increases with the magnitude of the inaccuracy.
• Until the defined error function stops changing or is stationary, or the optimum number of estimators is achieved, this whole process is repeated.

AdaBoost Classifier Example

Code

Output

0.0989747095010253

AdaBoost Regressor Example

Code

Output

The mean of the cross-validation scores:  0.7728539924062154
The average Score of KFold CV:  0.7966820925398042
The Mean Squared Error:  14.201356518866593
The Root Mean Squared Error:  3.768468723349922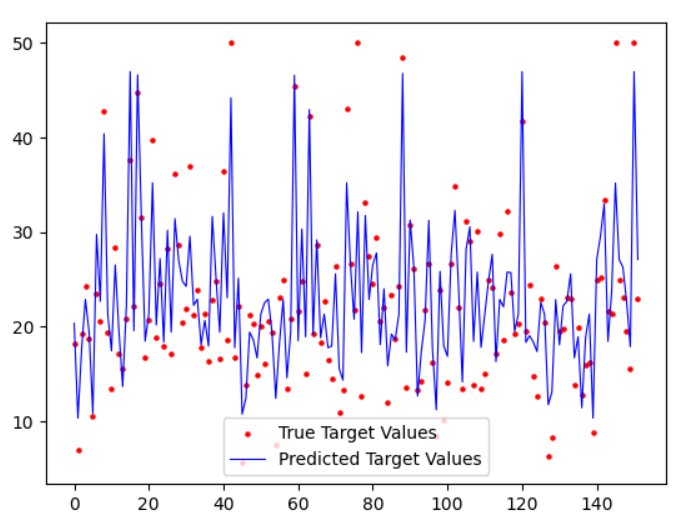

Bagging

Bagging is one of the Ensemble construction techniques, which is also known as Bootstrap Aggregation. Bootstrap establishes the foundation of the Bagging technique. Bootstrap is a sampling technique in which we select "n" observations from a population of "n" observations. But the selection is entirely random, i.e., each observation can be chosen from the original population so that each observation is equally likely to be selected in each iteration of the bootstrapping process. After the bootstrapped samples are formed, separate models are trained with the bootstrapped samples. In real experiments, the bootstrapped samples are drawn from the training set, and the sub-models are tested using the testing set. The final output prediction is combined across the projections of all the sub-models.

Bagging Classifier Example

Code

Output

0.9179254955570745

Bagging Regressor Example

Code

Output

Mean score and standard deviation:  -114.10792855309286 5.633321726584775