Python Tutorial
Python OOPs
Python MySQL
Python MongoDB
Python SQLite
Python Questions
Plotly
Python Tkinter (GUI)
Python Web Blocker
Python MCQ
Related Tutorials
Python Programs
GCD of two number in pythonGreatest Common Divisor (GCD) is a mathematical term to find the greatest common factor that can perfectly divide the two numbers. A GCD is also known as the Highest Common Factor (HCF). For example, the HCF/ GCD of two numbers 54 and 24 is 6. Because 6 is the largest common divisor that completely divides 54 and 24. 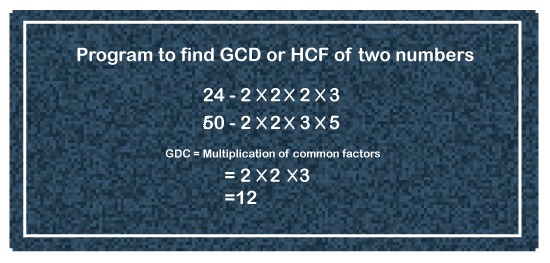
GCD Using gcd() FunctionIn python, a gcd() is an inbuilt function offered by the math module to find the greatest common divisor of two numbers. Syntax Where a and b are the two integer number passes as an argument to the function gcd(). Let's create a program to print the GCD of two number using the inbuilt function of math.gcd() in python. math_fun.py Output: 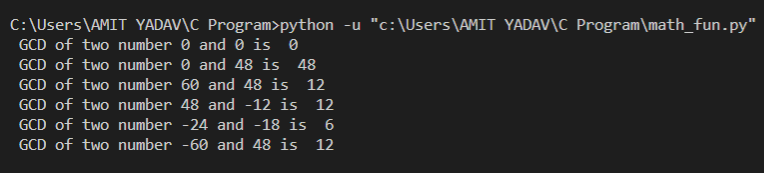
In the above example, math.gcd() function generates the GCD of two given numbers. In the gcd() function, a and b pass as an argument that returns the greatest common divisor of two integer numbers, completely dividing the numbers. GCD Using recursionRecursion is a memory consuming function defined in python that calls itself via self-referential expression. It means that the function will continuously call and repeat itself until the defined condition is met to return the greatest common divisor of the number. Pseudo Code of the AlgorithmStep 1: Take two inputs, x and y, from the user. Step 2: Pass the input number as an argument to a recursive function. Step 3: If the second number is equal to zero (0), it returns the first number. Step 4: Else it recursively calls the function with the second number as an argument until it gets the remainder, which divides the second number by the first number. Step 5: Call or assign the gcd_fun() to a variable. Step 6: Display the GCD of two numbers. Step 7: Exit from the program. Let's understand the program to find the GCD of two number using the recursion. gcdRecur.py Output: 
GCD Using the LoopLet's create program to find the GCD of two number in python using the loops. gcdFile.py Output: 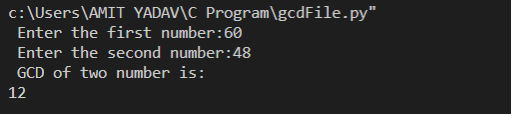
As we can see in the above program, we take two values as input and pass these numbers to the GCD_Loop () function to return a GCD. GCD Using Euclid's algorithm or Euclidean AlgorithmEuclid's algorithm is an efficient method to find the greatest common divisor of two numbers. It is the oldest algorithm that divides the greater number into smaller ones and takes the remainder. Again, it divides the smaller number from the remainder, and this algorithm continuously divides the number until the remainder becomes 0. For example, suppose we want to calculate the H.C.F of two numbers, 60 and 48. Then we divide the 60 by 48; it returns the remainder 12. Now we again divide the number 24 by 12, and then it returns the remainder 0. So, in this way, we get the H.C.F is 12. Pseudo Code of the Euclid AlgorithmStep 1: There are two integer numbers, such as a and b. Step 2: if a = 0, then the GCD(a, b) is b. Step 3: if b = 0, the GCD(a, b) is a. Step 4: a mod b find the Step 5: Suppose a = b and b = R Step 6: Repeat steps 4 and 3 until a mod b is equal or greater than 0. Step 7: GCD = b and then print the result. Step 8: Stop the program. Let's find the H.C.F or GCD of two numbers using Euclid's algorithm in python. Euclid.py Output: 
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










