Python Tutorial
Python OOPs
Python MySQL
Python MongoDB
Python SQLite
Python Questions
Plotly
Python Tkinter (GUI)
Python Web Blocker
Python MCQ
Related Tutorials
Python Programs
RSME - Root Mean Square Error in PythonThis tutorial will learn about the RSME (Root Mean Square Error) and its implementation in Python. Let's get started with its brief introduction. IntroductionRSME (Root mean square error) calculates the transformation between values predicted by a model and actual values. In other words, it is one such error in the technique of measuring the precision and error rate of any machine learning algorithm of a regression problem. Error metric allows us to track the various matrices' efficiency and accuracy. These matrices are given below.
Mean Square Error (MSE)MSE is a risk method that facilitates us to signify the average squared difference between the predicted and the actual value of a feature or variable. It is calculated using the below method. The syntax is given below. Syntax - Parameters -
Returns - It returns a non-negative floating point value (the best value is 0.0) or an array of floating point values, one for each individual target. Let's understand the following example. Example - 1 Output: The difference between actual and predicted values: 1.5388307249337076 Example - 2: Output: 3.15206 Root Mean Square Error (RMSE)RMSE is a square root of value gathered from the mean square error function. It helps us plot a difference between the estimate and actual value of a parameter of the model. Using RSME, we can easily measure the efficiency of the model. A well-working algorithm is known if its RSME score of less than 180. Anyhow, if the RSME value surpasses 180, we need to apply feature selection and hyper-parameter tuning on the model parameter. Root Mean Square Error with NumPy moduleRSME is a square root of the average squared difference between the predicted and actual value of the variable/feature. Let's see the following formula. 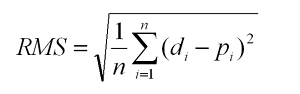
Let's breakdown the above formula -
We will implement the RSME using the functions of the Numpy module. Let's understand the following example. Note - If your system don't have numpy and sklearn libraries, you can install using the below commands.Example - Output: Root Mean Square Error: 2.127439775880859 Explanation - We calculated the difference between predicted and actual values in the above program using numpy.subtract() function. First, we defined two lists that contain actual and predicted values. Then we calculated the mean of actual and predicted values difference using the numpy's squre() method. Finally we calculated the rmse. ConclusionIn this tutorial, we have discussed how to calculate root square mean square using Python with illustration of example. It is mostly used to find the accuracy of given dataset. If RSME returns 0; it means there is no difference predicted and observed values.
Next TopicBuilding a Twitter Bot using Python
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










