Exponential Moving Average in Python

Moving averages are essential indicators when we need to find the trend of a stock or share for a specific period. Moving averages critically analyse the time series; thus, they are accommodating for economists, traders, and analysts to get insights about the market trend, identify the key performers and support levels, and track any stock's past and future performance.

Traders generally use moving averages at the entry and exit points and assist them in measuring trends, the strength of security in any transaction, and predicting the future trend of a stock.

Moving averages are of mainly three types. They are Simple Moving Average (SMA), Weighted Moving Average (WMA), and the Exponential Moving Average (EMA). SMA is the most basic one. It simply finds the average of the m data points where m is the given period of MA. Weighted Moving Averages provide weights to the data points involved in the SMA. EMA is also the same as WMA, as both types add more weight to the current or the most recent data.

EMA is a type of Weighted Moving Average. They give more weightage to the most recent data and hence track the performance of any stock over the given period. This makes these averages faster in reacting to the price changes in the given period.

Here we will learn more about the EMA and how to implement it in Python.

What Is the Exponential Moving Average?

EMA provides a measure to find the average price of a stock. It gives more weight to the current data points. Compared to SMA, EMA reacts to recent price movements more quickly and gives all observations made throughout the time the same weight.

Based on previous prices, the exponential moving average (EMA) is a technical indicator showing how a security's price is trending. Hence, EMAs are lag indicators that highlight the stock price pattern rather than forecasting future values.

The following elements should be taken into account while determining the EMA in the stock market:

• One should follow the same pre-defined rules when analysing the SMA and EMA in market analysis and trading.
• Compared to the SMA, the EMA measure is much more sensitive to even minor price changes and can identify the patterns in the market sooner than SMA.
• Since EMA are sensitive to price changes in the stock market, EMA is a prevalent measure to analyse short-term movements.
• With the EMA, we can understand the trend better and thus work toward the trend. In the stock market, one should consider purchasing a stock if the EMA of the stock is increasing, and if the EMA is decreasing, consider selling the stock.
• An EMA rise depicts that we should make a transaction, thus taking action, whereas if EMA decreases, it means we should not do any transaction; hence it resists action.
• EMA does not imply that it can reliably predict a trade's direction (up or down). However, it helps us to get an idea of the general direction of the trend but with a lag in the values at entry and exit points.

The formula for calculating the Exponential moving average (EMA)

Following is the formula to calculate the EMA: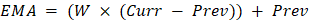

Steps to Calculate the EMA

Following are the steps to calculate the EMA:

Step 1 - Determine the simple moving average. Hence, if we wish to estimate the simple moving average for the previous ten days, add the latest ten values of the commodity and divide the total by 10.

For examples - 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 / 10 = 5.5

Step 2 - Using the following formula, compute the weighting constant to be multiplied by the difference for the particular number of periods:

EMA(current) = ((Price(current) - EMA (prev)) x Multiplier) + EMA(prev)

Step 3 - Now that you have both the SMA and the constant multiplier values, you can use the formula to compute the EMA:

(Closing price-EMA(previous day)) x multiplier + EMA(last day)

In this case, the EMA utilizes the prior day's readings and combines all price data into its current value. The influence of previous prices on moving averages is negligible, but the impact of new prices is maximal.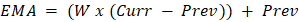

Curr = Current Value

Prev = Previous value of EMA

W = Exponential weighting constant

What Does the EMA Tell You?

EMA calculations are a good option for calculating moving averages of 10, 15, 20, 50, 100, and 200 days.

• Moving Average Convergence Divergence (MACD) and Percentage Price Oscillator (PPO) are calculated using the 12 and 25-day exponential moving averages (EMAs), which are regarded as short-term averages.
• The 50-day and 200-day EMAs are seen as indications of long-term trends.
• The traders can find the advantages of employing the perceptive EMA in analyzing stocks. Still, if the indications depicted by this moving average are mishandled, they can be damaging. Lag indicators, such as EMAs, confirm how the market acts at any time and tell how healthy or robust the market is.
• An EMA in trend analysis helps to lessen the negative impacts of lag since it prioritizes price activity and is more sensitive. This is an excellent method for determining a trade-entering indication.
• In trending markets, EMAs are helpful. The EMA in the direction of stocks and the shift ratio from one region to the next are useful to the trader. The EMA shows an upward pattern in a robust market and a downward trend in a weak market.
• A trader, for example, may be investing in a positive trend. Suppose he states a reverse or stability in the bullish trend with the assistance of EMA trends. In that case, it indicates that it is appropriate for him to move to another substantial investment.

We will now see how to calculate Exponential Moving Average in Python

EMA in Python

Method 1

We will not use any built-in library or function in this example. We will create our own algorithm to calculate EMA. We will create a small set of data values to use for reference.

Code

Output:

The EMA values are:
 [121, 117.64, 118.3, 115.98, 117.39, 118.96, 121.21, 122.27, 124.43, 125.15, 127.35, 129.49, 130.19, 131.82, 131.59, 133.1, 133.35, 134.93, 134.95, 136.36, 136.54]

Method 2

In this example, we will use the emw function of the Pandas library to calculate EMA. Let us first see the syntax of this function.

Syntax of the function

Here com = 1 / (1 + K), where K is the smoothening factor used in the formula to calculate EMA.

Example 1

We will calculate the EMA of our data values and plot the data and the moving average using the matplotlib library. Since the EMA is an average, it is the smoothened version of the actual time series data. We will take the com value as 2.5, which we have calculated for the K = 0.28. We can then compare the EMA values that we calculated using our algorithm and the EMA values calculated by the built-in ewm function.

Code

Output:

EMA:          Values
0   121.000000
1   114.000000
2   116.697248
3   114.110360
4   116.528432
5   118.660629
6   121.293028
7   122.429146
8   124.702267
9   125.382271
10  127.613872
11  129.762086
12  130.409649
13  132.021396
14  131.727681
15  133.241006
16  133.458575
17  135.045557
18  135.032519
19  136.453498
20  136.609775           

We can see that the EMA values are close to those we calculated earlier. Hence this proves that the algorithm gives a reasonable estimation of EMA.

Example 2

In this example, we will use the same time series we used in the previous example. However, we will see the effect on EMA after changing the com value.

Code

Output:

EMA:          Values
0   121.000000
1   114.333333
2   116.655738
3   114.401084
4   116.364112
5   118.162807
6   120.399265
7   121.504908
8   123.467316
9   124.258843
10  126.171358
11  128.067380
12  128.899659
13  130.385056
14  130.512530
15  131.847603
16  132.287999
17  133.655025
18  133.927954
19  135.156527
20  135.528654

Example 3

In this example, we will also use the same time series as before. Here we will give a different com value to the emw function. This time the value will be close to zero. We will see how such a small value will change the EMA calculation and will visualize it as we have done in the above cases.

Code

Output: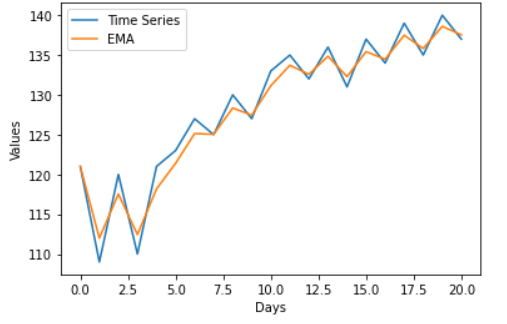

The Difference Between Exponential and Simple Moving Average

• Analysts and traders use the EMA and SMA to measure the time series trend by smoothing the raw data values. It helps in smoothening the fluctuations, which will make the analysis easier. Here are the main differences between the Simple Moving Average and the Exponential Moving Average.
• SMA is more inclined towards calculating the mean of the time series data for a particular period. However, EMA is inclined towards finding the present trend of the data.
• Another difference between these two is that EMA requires data of more than ten days to give a correct measure of 10-day EMA.
• Since EMA uses exponential weights for the data values, it is slightly more sensitive to fluctuations or changes in the data values. This makes it much more efficient to identify trends. Even faster than SMA. This property of EMA makes it very useful in stock market analysis. Since the results of the EMA will be up-to-date.
• SMA and EMA are important in calculating averages, but EMA estimates trends much faster than SMA. Therefore, EMA is more suitable for short-term analysis.

Limitations of the Exponential Moving Average

• A particular section of analysts believes that the current data should be emphasized in measuring trends as it adds more value. However, some analysts argue that overemphasizing the current data will introduce bias in the study, leading to more false positive cases.
• Another area for improvement of EMA is that it relies on past data, which usually does not talk about future trends.
• Based on EMA, we cannot decide whether a particular asset's value will increase or decrease in the future. Hence, it cannot predict the future trend of the attribute with certainty.
• It is prone to unwanted fluctuations in the values.