Acute Angle Definition

In the world of angles, an Acute Angle is a simple category of angles, followed by an Obtuse Angle (greater than 90 degrees), a Right Angle (equal to 90 degrees), and a Reflex Angle (more than 180 degrees). An acute angle is a type of angle that measures less than 90 degrees. In mathematical terms, an acute angle is defined as an angle with a measure between 0 and 90 degrees. In quadratic representation of angles on a plane, the first quadrant is occupied by acute angles (0 - 90), followed by the second quadrant of obtuse angles (90-180), the third quadrant (180 - 270), and last, that is fourth quadrant (270 - 360). This angle type is commonly found in geometry, trigonometry, and other mathematics, science, and economics areas. Acute angles play an important role in finding the relationships between the sides and angles of shapes.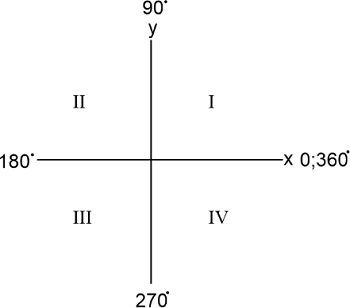

Acute angles can be found in many real-world objects and shapes, such as triangles, polygon shapes, and clock hands. When two line segments intersect to form an angle, the angle can be measured in degrees to determine if it is acute. Examples of acute angles are 27 degrees, 45 degrees, 67 degrees, 15 degrees, and 40 degrees.

Different Types of Angle

Obtuse Angle: An obtuse angle is an angle with a measure greater than 90 degrees but less than 180 degrees. It is often described as a wide or open-angle and is the opposite of an acute angle. Obtuse angles can be found in various shapes such as triangles, polygon shapes, and clock hands. In mathematics and geometry, obtuse angles play an important role in finding the relationships between the sides and angles of shapes. When two lines intersect to form an angle, the angle can be measured in degrees to determine whether it is obtuse. Understanding obtuse angles are essential in solving problems in fields such as engineering, architecture, and cartography, where it is important to measure and analyze angles accurately. Obtuse angles can also determine if a triangle is an obtuse triangle with one angle greater than 90 degrees. Examples of obtuse angles are 102 degrees, 100 degrees, 175 degrees, and 175 degrees.

Right Angle: A right angle is a type of angle that measures exactly 90 degrees. It is often symbolized by a small square placed at the angle's vertex. A right angle is considered a perpendicular angle, meaning that two lines that form a right angle are perpendicular to each other or at a 90-degree angle. In geometry, right angles are crucial in defining shapes and their properties. For example, in a rectangle and a square, all four angles are right angles. Understanding right angles are essential in solving engineering, architecture, and cartography problems, where measuring and analysing angles and shapes is important. Right angles are also used in trigonometry, which forms the basis for many calculations and formulas.

Reflex Angle: A reflex angle is an angle that measures greater than 180 degrees and less than 360 degrees. It is often referred to as a "turning angle" as it goes beyond a straight line and completes a full turn. Reflex angles complement acute and obtuse angles, as their measures add up to 360 degrees. In geometry, reflex angles play an important role in finding the relationships between the sides and angles of shapes. They are often used in engineering and cartography, where measuring and analyzing angles is important. Reflex angles are also used in trigonometry, describing circular functions and the relationships between angles and their corresponding values. When two lines intersect to form an angle, the angle can be measured in degrees to determine whether it is a reflex angle. Understanding reflex angles is essential in solving problems involving angles and shapes in real-world applications. Examples of reflex angles are 270 degrees, 190 degrees, 250 degrees, and 300 degrees.

Acute Angles are Important in Many Real-World Applications

• The acute angle is used in surveying.
• The acute angle is used in navigation.
• The acute angle is used in construction.
• The acute angle is used in engineering.
• The acute angle is used to learn how angles directly relate to the shapes.

For example, in surveying, an acute angle can be used to determine the height of a building or other structure. In navigation, acute angles are used to determine the direction and position of ships in the sea and the direction and position of planes in the air. In construction, acute angles are used to make an exact calculation of walls and bricks for making a smooth building. In engineering, acute angles are used as a mathematical tool to solve complex mathematical problems.

In geometry, acute angles define the shape and size of figures such as triangles, squares, rectangles, and other polygons. For example, an acute angle measures less than 90 degrees in a triangle, while an obtuse angle measures greater than 90 degrees. Triangles with three acute angles are known as acute triangles, which are important in determining the shape and size of other figures, such as circles and cones.

In trigonometry, acute angles are used to calculate an angle's sine, cosine, and tangent. These trigonometric functions are important in many areas of science and engineering, including physics, astronomy, and computer graphics.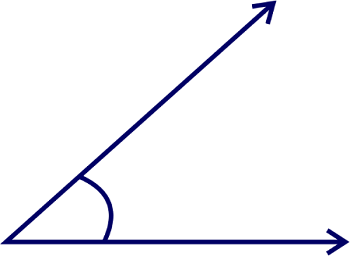

Solved Examples Based on the Acute Angle

Example 1: Find the measure of an acute angle that is one-third of a right angle.

Solution: A triangle is a shape that has three sides and three angles; in a right-angled triangle, an angle must measure 90 degrees, so one-third of a right angle is 90 / 3 = 30 degrees. Thus, an acute angle of one-third of the right-angle measures 30 degrees.

Example 2: Two angles measure 30 and 60 degrees in a triangle. What is the measure of the third angle?

Solution: The sum of the angles in a triangle is always 180 degrees, so we have 30 + 60 + x = 180, where x is the third angle measure. Solving for x, we get

x = (180 - 90) degrees

x = 90 degrees

so the third angle of the given triangle measures 90 degrees.

Example 3: In a triangle, one angle measures 75 degrees, and another measures 60 degrees. What is the measure of the third angle?

Solution: The sum of the angles in a triangle is always 180 degrees, so we have 75 + 60 + x = 180, where x is the third angle measure. Solving for x, we get

X = (180 - 135)

x = 45 degrees

so the third angle measures 45 degrees.

Example 4: What is the sine of an acute angle that measures 30 degrees?

Solution: Using a calculator or a trigonometry table, we find that the sine of 30 degrees is 1 / 2, which is 0.5 in decimal. Thus, the sine of an acute angle that measures 30 degrees is 0.5.

Example 5: What is the cosine of an acute angle that measures 60 degrees?

Solution: Using a calculator or a trigonometry table, we find that the cosine of 60 degrees is 1 / 2, which is 0.5 in decimal. Thus, the cosine of an acute angle that measures 60 degrees is 0.5

Example 6: Find the complement of an acute angle of 40 degrees.

Solution: The complement of an angle is 90 degrees minus the angle's measure. So, the complement of 40 degrees is 90 - 40 = 50 degrees.

Example 7: Find the complement of an acute angle of 60 degrees.

Solution: The complement of an angle is 90 degrees minus the angle's measure. So, the complement of 60 degrees is 90 - 60 = 30 degrees.

Example 8: Find the supplement of an acute angle of 50 degrees.

Solution: The supplement of an angle is 180 degrees minus the angle's measure. So, the supplement of 50 degrees is 180 - 50 = 130 degrees.

Example 9: Find the supplement of an acute angle of 75 degrees.

Solution: The supplement of an angle is 180 degrees minus the angle's measure. So, the supplement of 75 degrees is 180 - 75 = 105 degrees.

Example 10: If two acute angles measure 35 degrees and 55 degrees, find the measure of their sum.

Solution: The sum of two angles is just the addition of their measures, so the sum of 35 degrees and 55 degrees is 35 + 55 = 90 degrees.

In conclusion, acute angles are a fundamental concept in mathematics and science and are essential in many real-world applications. Whether in surveying, navigation, construction, engineering, or any other field, acute angles play a critical role in determining the shape, size, and position of objects and structures.