Random Variable Definition

Introduction to Random Variables

A random variable is a mathematical function that assigns a numerical value to every outcome which is possible in a random experiment. It is called a random variable because its value depends on the output of a random experiment. Random variables are usually symbolized by capital letters, such as X, Y, or Z.

For example, let's consider the outcome of flipping a coin. If the coin lands head, we assign a value of 1 to the random variable X, and if it lands tails, we assign a value of 0 to X. Therefore, X is a random variable that takes on two possible values, 0 or 1, depending on the outcome of the coin flip. We can represent the possible values of X using a probability distribution, which tells us the probability of each possible value.

For the case of tossing a coin, the probability distribution is as follows:

• P(X = 0) = 1 / 2 (since the probability of getting tails is 1 / 2)
• P(X = 1) = 1 / 2 (since the probability of getting heads is also 1 / 2)

In general, a probability distribution for a random variable specifies the probability of each possible value of the variable.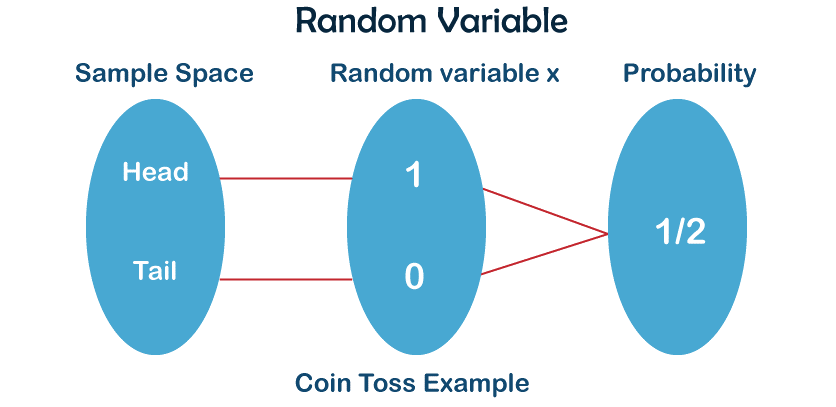

Definition of Random Variable

A random variable is a mathematical function that maps each output of a random experiment to a numerical value. More specifically, a random variable X is a random function that maps each outcome in the sample space S to a real number. That is,

X: S to R,

Where R symbolizes the set of real numbers, the values that X can take on are called the range of X.

History

Random variables have a long and rich history in mathematics and statistics, dating back to the 17th century. The concept of probability, which forms the foundation for random variables, was first studied by mathematicians such as Blaise Pascal and Pierre de Fermat.

In the 18th and 19th centuries, mathematicians such as Laplace and Gauss further developed the theory of probability and introduced the idea of a continuous probability distribution. However, it was not till the 20th century that the concept of a random variable was formally defined and used in modern statistics.

In 1900, the mathematician Georg Cantor introduced the concept of a sample space, which is the set of all possible outcomes of a random experiment. This led to the rise of the concept of a random variable, which is a variable that takes on different values depending on the outcome of a random experiment.

In the early 1900s, the statistician Karl Pearson introduced the concept of a probability density function, which describes the probability distribution of a continuous random variable. Later, other mathematicians and statisticians such as Ronald Fisher, Jerzy Neyman, and Abraham Wald further developed the theory of random variables and their applications in statistics.

Well, to put it simply, we can say that it is not confirmed who discovered the concept of Random Variables but many historians and mathematicians believed that Pafnuty Chebyshev (a Russian Mathematician also known as the 'founding father of Russian Mathematics ) was the first person "to think systematically in terms of random variables".

Today, random variables are a fundamental concept in probability theory and statistics and are used in a wide range of fields, including finance, engineering, physics, and biology. The study of random variables continues to be an active area of research in mathematics and statistics, with new applications and extensions of the theory being developed all the time.

Types of a Random Variable

There are two specific types of Random variables:

1. Discrete Random variables
2. Continuous Random variables.

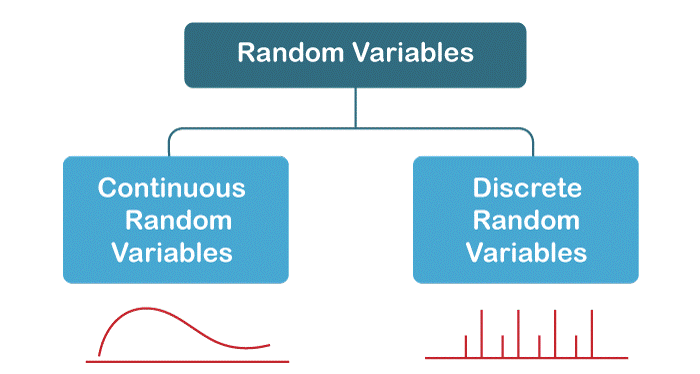
1. Discrete Random Variables: Discrete random variables take on a finite or accountably infinite set of possible values. In other words, the range of a discrete random variable is a discrete set of numbers. For example, the number of heads obtained when flipping a coin five times is a discrete random variable that can take on values 0, 1, 2, 3, 4, or 5.

The probability distribution for a discrete random variable is called a probability mass function (PMF). The PMF gives the probability that the random variable takes on a particular value.

For example, consider the random variable X which represents the number of heads obtained when flipping a fair coin three times. The PMF for X is:

• P(X = 0) = 1/8 (since there is only one way to get no heads: TTT)
• P(X = 1) = 3/8 (since there are three ways to get one head: HTT, THT, TTH)
• P(X = 2) = 3/8 (since there are three ways to get two heads: HHT, HTH, THH)
• P(X = 3) = 1/8 (since there is only one way to get three heads: HHH)

Note that the probabilities in the PMF must sum to 1 since the random variable must take on one of the possible values.

2. Continuous Random Variables: The Continuous random variables take on any value in a continuous range of possible values. In other words, the range of a continuous random variable is an uncountable set of numbers. For example, the height of a person can be referred to as a continuous random variable that can take on any value in a continuous range from zero to infinity. The probability distribution for a continuous random variable is called a probability density function (PDF). Unlike the PMF, the PDF does not give the probability that the random variable takes on a particular value, but rather the probability density at each point in the range of possible values. The probability density can be thought of as the height of a curve at a particular point on the x-axis, and the total area under the curve must equal 1.

Parts of Random Variables

Random variables can be classified in different ways, depending on the properties that we are interested in. Some common classifications of random variables are:

1. Bernoulli Random Variable: A Bernoulli random variable can be defined as a discrete random variable that takes on only two possible values, 0 or 1. It is used to model a single trial with two possible outcomes, such as flipping a coin or rolling a dice.
2. Binomial Random Variable: A Binomial Random variable can be defined as a discrete random variable that measures the number of successes in a fixed number of independent trials, where each trial has only 2 possible outcomes and the probability of success is constant. It is used to model situations such as the number of heads in a fixed number of coin flips or the number of defective items in a batch of products.
3. Poisson Random Variables: A Poisson random variable is a discrete random variable that measures the number of occurrences of a rare event in a fixed time interval, assuming that the events occur independently and at a particular rate. It is used to model situations such as the number of consumers arriving at a shop in a fixed time interval or the number of defects in a product.
4. Normal Random Variables: A Normal Random variable can be defined as a continuous random variable that follows a particular normal distribution, which is a bell-shaped distribution characterized by its mean and variance. Normal random variables are widely used in statistical analysis and inference, as many natural phenomena and processes follow a normal distribution.
5. Exponential Random Variables: An Exponential Random variable can be defined as a continuous random variable that measures the time between two consecutive events in a Poisson process. It is used to model situations such as the time between the arrival of customers at a store or the time between failures of a machine.

Properties of Random Variable

Random variables have several important properties that help us understand and analyze their behaviour. Here are some of the most important properties of random variables:

1. Mean (Expected Value): The mean of a random variable, denoted E(X) or ?, is the average value of the variable over many trials. For a discrete random variable, the mean is calculated by summing the product of each possible value and its corresponding probability. For a continuous random variable, the mean is calculated using an integral. The mean is an important measure of central tendency and gives us a sense of where the variable tends to cluster.
2. Variance: The variance of a random variable denoted by Var(X) or sigma�, measures the spread of the variable around its mean. A high variance indicates that the variable tends to deviate from its mean, while a low variance indicates that the variable tends to stay close to its mean. The variance is calculated by taking the sum of the squared deviations of each possible value from the mean, weighted by their corresponding probabilities (for a discrete random variable) or by integrating the squared deviations over the range of possible values (for a continuous random variable).
3. Standard Deviation: The standard deviation of a random variable denoted by SD(X) or sigma is the square root of its variance. The standard deviation is a common measure of variability and gives us a sense of how much the variable tends to deviate from its mean.
4. Cumulative Distribution Function (CDF): The CDF of a random variable X, denoted F(x), gives the probability that X is less than or equal to a given value x. The CDF is a cumulative measure of the probability distribution and can be used to calculate probabilities for specific intervals of X.
5. Moment Generating Function (MGF): The MGF of a random variable X, denoted M(t), is a function that can be used to derive various moments (such as the mean and variance) of the distribution of X. The MGF is defined as the expected value of e^(t.X), where t is a parameter. The MGF is useful for finding moments because it can be differentiated to obtain the moments directly.

Applications of Random Variables: An Overview

Random variables are mathematical constructs used to model the outcomes of random events. They play a fundamental role in probability theory and statistics and have a wide range of applications across different fields. In this description, we will provide an outlook of some of the key applications of random variables.

1. Probability Theory: In probability theory, random variables are used to model the outcomes of random experiments. For example, when flipping a coin, the outcome can be either heads or tails, and each outcome has a probability of 0.5. The random variable X can be defined to be the number of heads that appear in a given number of coin flips. X can take on discrete values, such as 0, 1, or 2, and its distribution can be described by the binomial distribution.
2. Statistics: In statistics, random variables are used to describe the distribution of a dataset. For example, the heights of a group of people can be modelled by continuous random variables, and its distributions can be described by a probability density function, the Random variables can also be used to calculate expected values and probabilities. The anticipated value of a random variable is the average value it would take on over a large number of trials, weighted by their probabilities.
3. Economics: In economics, random variables are used to model uncertain events, such as the price of a stock or the demand for a product. Random variables are also used to model the behaviour of agents in a market, such as buyers and sellers. The distribution of a random variable can be used to estimate the probability of certain outcomes, which can help decision-makers to make better-informed choices.
4. Engineering: In engineering, random variables are used to model the behaviour of systems that are subject to uncertainty, such as the lifespan of a machine or the load on a bridge. Random variables are also used in reliability analysis to estimate the probability of failure of a system under different conditions. Random variables can be combined using mathematical techniques such as convolution to model more complex systems.
5. Physics: In physics, random variables are used to model the behaviour of particles and systems that are subject to probabilistic phenomena, such as the decay of radioactive isotopes or the diffusion of particles. Random variables can also be used to model the noise in a signal or measurement and to estimate the uncertainty in experimental data.

So overall, we can say that Random Variables have numerous applications across different fields, from probability theory and statistics to economics, engineering, and physics. Understanding the properties and behaviour of random variables is essential for modelling and analyzing uncertain events and systems.