Integers Definition and Examples

What is an Integers

It is a set of wholes containing all positive and negative numbers devoid of fractional or decimal parts. The letter used for the denoting Integer is Z, and it includes ( -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10)

Integers are used for conducting mathematics operations such as addition, subtraction, multiplication, and division. Integers are used in diverse fields such as economics, mathematics, computer programming, and science.

Types of Integers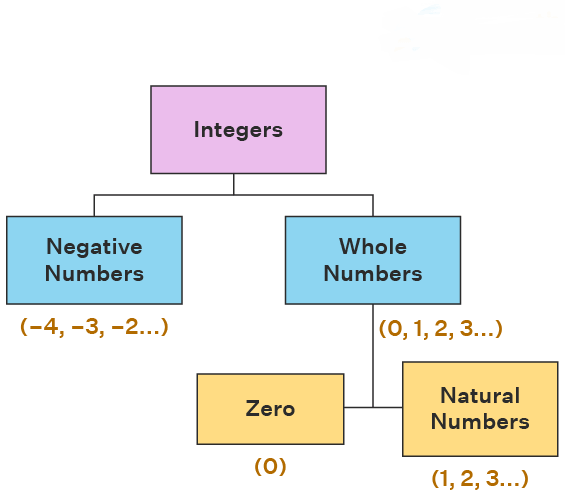

• Zero: Zero is regarded as neither a positive nor negative integer. It is said as a neutral number. Therefore, it does not have any sign.
• Positive Integers: They are termed natural numbers or counting numbers. These integers are sometimes represented with the symbol Z+. They are all represented on the positive side of the number line. For example
  1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30.
• Negative Integers: These integers are represented on the left side of the number line. The Z- denotes them- sign.
  -1, -2, -3, -4, -5, -6, -7, -8, -9, -10.

Representation of the Integers on the Number Line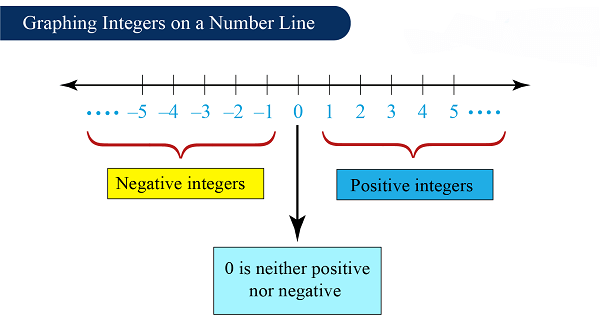

It has already been mentioned that three types of integers exist, and it is very easy to represent them on the number line depending upon the negative and positive integers on the zero.

Zero is sitting in the center of the number line. Positive integers are placed on the right side of the zero, and negative integers are placed on the left side of the zero.

Rules of the Integers

Since integers are whole numbers, they can be Zero, Negative and positive. They abide by specific rules and properties that control their behavior in mathematic operations. Some general rules used in the integers are:

1. Addition of Integers

• Addition of two Positive Numbers

When two positive numbers are added, the result is a positive integer.

For example

4 + 3 = 7

7 + 3 = 10

• Addition of Two Negative Numbers

When two negative numbers are added, the given result would be negative integers. For say

(-3) + (-4) = (-7)

(-5) + (-5) = (-10)

• Addition of Positive and Negative Integer

When a positive integer is added to a negative integer, the result will be based on the magnitude of the number. If a positive number is greater, the result would also be positive. If the negative integer has a larger magnitude, the result would be a negative integer. For example

(-6) + 7 = 1

(-8) + 4 = -4

2. Subtraction of Integers

• Subtraction of Two Positive Integers

This mathematical operation executes by subtracting the smaller integer value from the large value of the integer. The sign of the result is equal to the larger integer. On the other sense,

x - y = z, where x > y for example, 7 - 6 = 1.

• Subtraction of a Positive Integer from a Negative Integer

To subtract a positive integer from a negative integer, the positive integer should be added to the absolute value of the negative integer and keep the positive sign of the result. In other words,

x - (-y) = z where z > 0.

For example, 4 - (-5) = 9

• Subtraction of Two Negative Integers

For the subtraction of two negative numbers, change the subtraction operation to the addition, alter the sign of the second negative integer to positive, and then carry out the addition as usual. In another sense,

-a - (-b) = c where a > 0 and b > 0.

For example, -7 - (-3) = -4

Above are the rules for the subtraction of the integers. It is crucial to understand the working of the sign of the integers during subtraction to perform the operation correctly and get the correct result.

3. Multiplication of the Integers

The rules which are observed in the multiplication of the integers:

• Multiplication of the Two Positive Integers

In the multiplication of two positive integers, use simple multiplication rules, and the result will be a positive integer. In another sense,

xb = z, where a > 0 and b > 0.

For example, 5 * 4 = 20.

• Multiplication of a Positive Integer by a Negative Integer

For the multiplication of the positive integers by negative integers, multiply them together, and the result obtained will be a negative integer. This can be illustrated:

a x (-b) = -c, where a > 0 and b > 0

Example: 5 x (-2) = -10

• Multiplication of a Negative Integer by a Positive Integer

For the multiplication of a negative integer by a positive integer, multiply them together, and the result obtained will be a negative number. This is illustrated below

(-a) x b = -c, where a > 0 and b > 0

Example: (-3) * 6 = -18

• Multiplication of the Negative Integers

Multiplying two negative numbers together, and the result obtained will be a positive integer. This is illustrated below.

(-a) x (-b) = c, where a > 0 and b > 0

Example: (-2) * (-3) = 6

• Multiplication With Zero Value

The result will always be zero when a number is multiplied by zero. It is independent of the sign of the integer.In other words:

x 0 = 0, where a is any integer

Example: 7 x 0 = 0

Above are the rules for the multiplication of the integer. It's important to understand these rules to perform multiplication operations with integers correctly and obtain the correct results.

4. Division of the Integers

• Division of the Positive Integers

Normal Division: Divide the dividend by the divisor. When the two positive integers are given, the result obtained from the operation will be a positive integer or will be in the form of a fraction. In other words:

a / b = c, where a > 0 and b > 0

Example: 8 / 4 = 2

• Division of the Positive Integer by the Negative Integer

Divide the dividend by the negative integer, and the result obtained from the operation will be a negative integer or a fraction. This can be illustrated as:

a / b = c, where a > 0 and b > 0

Example: 12 / -3 = -4

• Division of a Negative Integer by a Positive Integer

Divide the dividend by the positive integer. The result obtained will be a negative integer. For example

a / b = c, where a > 0 and b > 0

-8/(4) = -2

• Division of the Two Negative Integers

The result always turns positive when the division occurs between two negative integers.

a / b = c, where a > 0 and b > 0

-8/ -4 = 2

Some Main Properties of Integers

1. Commutative Property

The commutative property governs the addition of the integers. It implies that when the order of the integers when they are added, it does not affect the result.

a+b=b+a

4+ 5 =5+4

9=9

2. Zero Property

Adding the value of zero to the integer does not alter the value of the integer. For example

4 + 0 = 4

(-3) + 0 = (-3)

3. Associative Property

The law of the associative property also governs the addition of the integers. The property states that adding the number to the group does not alter the result.

(6 + 7) + 5 = (7 + 5) + 6

18=18

4. Identity Property of the Integers

The identity element property of the integers says that a unique property character exists, referred to as an "identity element" or additive identity, such as that when a number is added to it, the outcome would be the result itself. We can understand that identity characteristic is a characteristic that does not alter the value of the other elements when added to them.

Mathematically, the identity element property of addition can be expressed as follows:

For any integer 'a',

a + 0 = 0 + a

= a

This is valid for all integers, such as positive, negative, and zero.

Multiplicative Inverse of an Integers

The multiplicative Inverse of a non-zero integer is a number that, when a number is multiplied by the original integer, gives the product of 1. In other words, for an integer "a," its multiplicative inverse "b" is such that "a" multiplied by "b" equals 1.

The presence of the multiplicative Inverse relies upon the original integer being zero. For the non-zero integers, a unique multiplicative inverse exists, which is also an integer. However, for the integer 0, there is no multiplicative inverse, as division by zero is undefined in mathematics.

Formally, for a non-zero integer "a," its multiplicative inverse "b" can be expressed as:

a * b = 1

Solving for "b" gives:

b = 1/a

For example, let's consider the integer 4. The multiplicative inverse of 4 would be 1/4, because 4 multiplied by 1/4 equals 1:

4 * (1/4) = 1

Similarly, the multiplicative inverse of -2 would be -1/2, because -2 multiplied by -1/2 also equals 1:

-2 * (-1/2) = 1

The point should be remembered that all integers do not contain any multiplicative inverse. For example, no integer value may be multiplied by 0 to produce 1. Therefore, 0 will not be considered a multiplicative inverse.