Square Definition

A square is defined as a quadrilateral having four equal sides. Several things in our surroundings have a square shape. It has equal sides, and internal angles are 90 degrees in each square shape. Its opposing sides are perpendicular to one other. You can find many items in your surroundings that have a square shape. The chessboard, craft sheets, bread slice, picture frame, mirror, pizza box, wall clock, etc., are common representations of this shape.

The Square's basic shape can be seen below.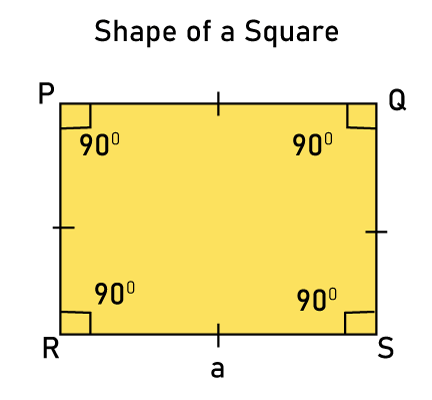

Properties of Square

The following is a list of a square's most significant characteristics:

A square is a quadrilateral with four sides and four vertices.
The square's four sides are equal in length.
The square's opposite sides are always parallel.
The square has a 90° internal angle for each vertex.
The sum of all internal angles = 360°.
At a 90° angle, the square's diagonals meet.
Each diagonal is the same length.
The parallel sides of a square make it a parallelogram as well.
A square has longer diagonals than sides.
Two equal triangles are formed by diagonally dividing the square.
A square's internal angle is divided in half by its diagonal, creating two adjacent 45° angles.

Rectangle and Square Common Properties

A square and a rectangle share several properties. The points below depict all of the common features that constitute a rectangle & a square.

Due to their four sides & four vertices, the square and the rectangle are quadrilaterals.
Each inner angle of a square & rectangle is 90°.
The sum of a square's and a rectangle's internal angles equals 360°.
A diagonal separates a square & a rectangle into two right-angled triangles.
Due to parallel opposite sides, squares and rectangles are often known as parallelograms.

Formulas

A square has four equal sides, as we all know. In geometry, three main square formulae are often used. First, calculate the area, then the perimeter, and last, use the square formula to calculate the diagonal. Let's examine these square formulas in more detail.

Area of Square

The area of a square is the region it covers on a two-dimensional plane or the space it occupies. The area can be calculated using the formula Area of Square = , where 's' is the Square's side. It is measured in sq. units such as , , & so on.

Area = per square unit

Perimeter of Square

A square's perimeter is the whole length of its boundaries. Hence the Square's perimeter can be calculated by adding the lengths of each side. Because a square has four sides, we need to sum up all four sides of a square to determine its perimeter.

We can calculate the length of a square's border using the perimeter formula. Square perimeter = side +side + side + side. It is measured in units such as cm, m, inches, & so on.

Perimeter of Square = 4 × side

Diagonal of a Square

The diagonal is the segment of a line between two non-adjacent vertices of a square. The following Square's diagonals are represented by AC & BD. As you can see, lines AC and BD are the same lengths. The square is divided into two equal triangles by a diagonal, with the diagonals forming the hypotenuse from each resulting right-angled triangle.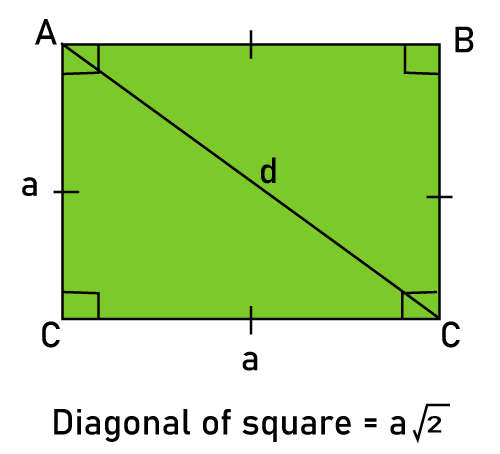

Let's examine the process used to calculate the Square's diagonal formula. Let 'a' denote the side length and 'd' denote the diagonal length of a square, using the example square above as an example. For the triangle, we can apply the Pythagoras theorem. ADC: d²=a²+a²

The result of taking the square root of both sides is √(d²)=√(2a²)

Formula-

Diagonal of Square (d)= √2 × a