Polygon definition

In this article, we are going to discuss polygon's definition. The topic is not limited to polygon's definition; here, we will also discuss the examples, shapes, types, polygon properties, and some FAQs.

Definition of polygon

A polygon is defined as a 2D closed geometric figure that has a finite number of sides. It is formed using a collection of lines. The lines that are used to form a polygon are called as sides or edges. The points where line segments are connected are called as corners or vertex. Examples of polygon are triangle, pentagon, hexagon, and many more.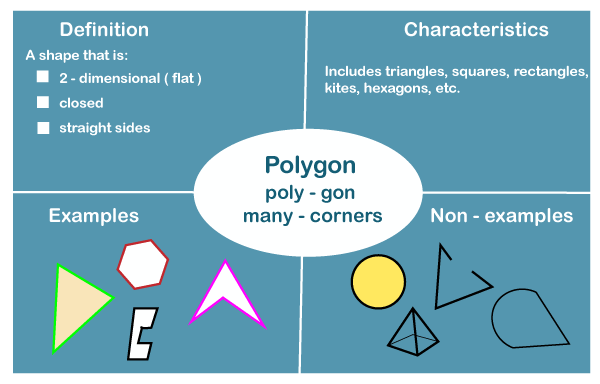

There is no curve side is present in a polygon. Despite a plane figure, a circle is not considered as a polygon. It is because the circle is a curved shape that does not have any sides or angles. We can say that not all 2D figures are polygons.

To form a closed figure, three line segments need to be joined together. A polygon with atleast three sides is called as triangle and also referred to as 3-gon. Similarly, an n-sided polygon is referred to as n-gon.

Now, let's discuss the types of a polygon.

Types of polygon

The polygons are classified into various types based on the angles and sides. The types of polygons are listed as follows -

• Regular polygon
• Irregular polygon
• Concave polygon
• Convex polygon

Now, let's discuss each of the polygon types.

Regular polygon

If all the sides and interior angles of a polygon are equal, the polygon is said to be the regular polygon. Examples of the regular polygon include equilateral triangle, rhombus, square, and many more. In the below image, you can see examples of regular polygon.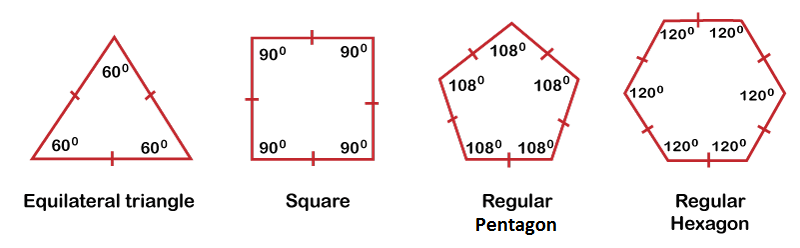

Irregular polygon

If all the sides and interior angles of a polygon are of different measure, the polygon is said to be the irregular polygon. Examples of the irregular polygon include rectangle, kite, scalene triangle, and many more. In the below image, you can see examples of an irregular polygon.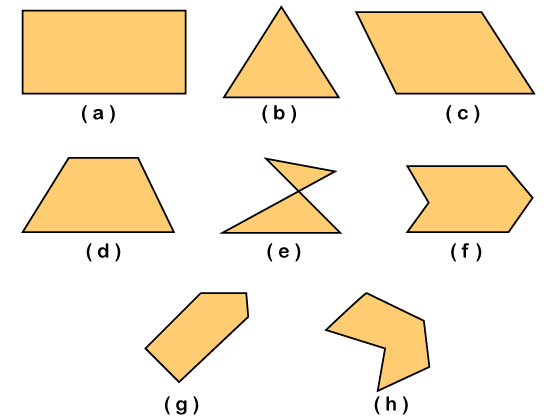

Convex polygon

A polygon is said to be the convex polygon if its interior angles are strictly less than 180 degrees. In a convex polygon, the vertex points outer from the center of the shape. In the below image, you can see the example of a convex polygon.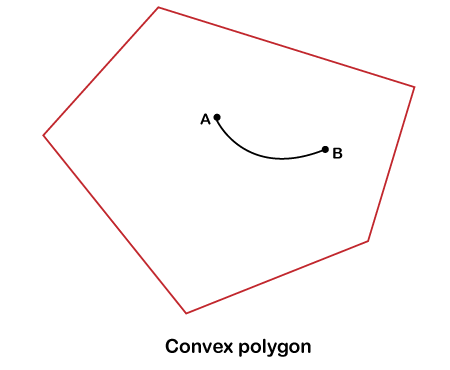

Concave polygon

A polygon is said to be the concave polygon if one or more interior angles of the polygon are more than 180 degrees. A concave polygon has one interior angle greater than 180°. So that it can be clipped into similar polygons. In a concave polygon, the vertex point towards the polygon's inside. In the below image, you can see the example of concave polygon.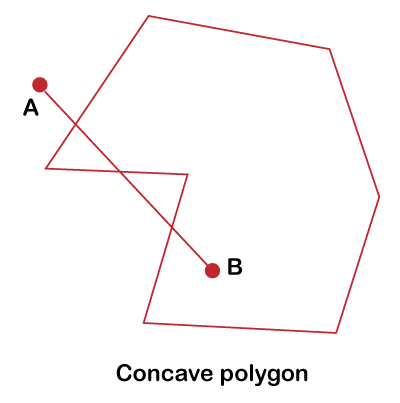

Angles of polygon

In a Polygon, the number of vertices is equal to the number of sides. Every corner has a definite measure of angles that are divided into two categories: interior angles and exterior angles. Let's separately discuss both types of angles.

Interior angle property

The sum of all interior angles of an n-gon (polygon with 'n' number of sides) is = (n - 2)∏ radians

Or, (n - 2) x 180⁰

Where 'n' in the above formula is the number of sides of a polygon.

As an instance, suppose there are four sides in a quadrilateral, so the sum of interior angles of that quadrilateral is = (4 - 2) x 180⁰

= 360⁰

Exterior angle property

The exterior angle is the supplementary angle to the interior angle. In a polygon, the sum of all exterior angles is equal to 360⁰.

The sum of the interior angle and its corresponding exterior angle is equivalent to 180⁰ degrees -

Exterior angle + Interior angle = 180⁰

Or, Exterior angle = 180⁰ - Interior angle

Let's see some of the properties of a polygon.

Properties of polygon

There are some of the properties of a polygon that are listed as follows -

• A polygon that has 'n' number of sides has the number of diagonals = n(n - 3)/2
• The sum of all interior angles of an n-gon (polygon with 'n' number of sides) is = (n - 2)∏ radians
  Or, (n - 2) x 180⁰
• On joining the diagonals from one corner of a polygon, the number of triangles formed is = n - 2 (where 'n' is the number of sides)
• In an n-sided regular polygon, the measure of each interior angle is = [(n - 2) x 180⁰]/n
• In an n-sided regular polygon, the measure of each exterior angle is = 360⁰/n

Now let's discuss some questions related to the polygon.

Questions and answers related to polygon

Question 1 - What will be the value of x in the below figure?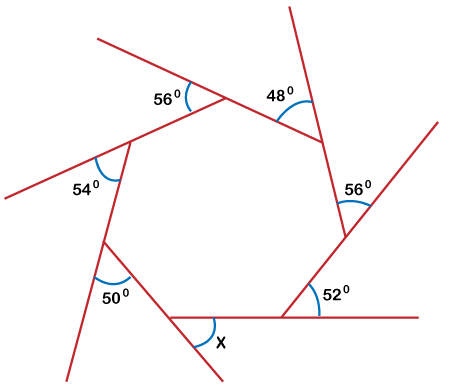

Answer 1 - In the given figure, there are exterior angles, and x is also an exterior angle. We know that, in a polygon, the sum of all exterior angles is equal to 360⁰. So, let's calculate the value of x by using this property of exterior angle.

Thus, 56⁰ + 54⁰ + 50⁰ + x + 52⁰ + 56⁰ + 48⁰ = 360⁰

316⁰ + x = 360⁰

x = 360⁰ - 316⁰

= 44⁰

So, the value of the x in the given image is 44⁰.

Question 2 - What will be the sum of interior angles of a regular hexagon?

Answer 2 - A regular hexagon has 6 sides. So, we know that,

The sum of all interior angles of an n-gon (polygon with 'n' number of sides) is = (n - 2) x 180⁰

Thus, (6 - 2) x 180⁰ = 720⁰

So, the sum of interior angles of a regular hexagon is 720⁰.

Question 3 - What is the value of the interior angle of a regular hexagon?

Answer 3 - In the above solution, we have seen that the sum of interior angles of a regular hexagon is 720⁰, and a regular hexagon has six equal interior angles.

So, the value of the interior angle of a regular hexagon is 720⁰ ÷ 6 = 120⁰.

Now, let's discuss some of the frequently asked questions (FAQs) related to the polygon.

Frequently Asked Questions (FAQs)

Question 1 - What is a polygon?

Answer 1 - A polygon is defined as a 2D closed geometric figure that has a finite number of sides. It is formed using a collection of lines.

Question 2 - Can a polygon have curved sides?

Answer 2 - A polygon does not have any curved sides. Despite a plane figure, a circle is not considered as a polygon. It is because the circle is a curved shape that does not have any sides or angles.

Question 3 - How many diagonals are there in a polygon?

Answer 3 - A polygon that has 'n' number of sides has the number of diagonals = n(n - 3)/2. It is important to note that triangles do not have diagonals.

Question 4 - A polygon with 5 sides is known as -

Answer 4 - A polygon with 5 sides is known as a pentagon. It also has 5 diagonals and 5 vertices.

Question 6 - A polygon with 7 sides is known as -

Answer 6 - A polygon with 7 sides is known as heptagon. It also has 14 diagonals and 7 vertices.

Question 7 - Is a cube is polygon?

Answer 7 - No, cube is not considered as a polygon. A cube is a three-dimensional shape, whereas a polygon is two dimensional. So, cube is not considered as a polygon.

Question8 - Is star is polygon?

Answer 8 - Yes, the star is considered as a polygon. In geometry, it is known as star polygon.

So, that's all about polygons. Hope this article is beneficial for you and provided you the information about polygons.