Average Velocity Definition

Average velocity is a topic in physics (a branch of science) that describes the displacement covered by an object over a certain interval of time. This calculation is often used in scientific and engineering applications to calculate speed and distance. It plays a crucial role in understanding the movement of objects in space and time. Let us discuss average velocity in detail in this article.

Velocity is the rate at which an object changes its relative position in a given period. It is calculated as the distance an object travels divided by the time taken to travel that distance. The term "average" in average velocity refers to the total displacement of an object over a period divided by the time taken.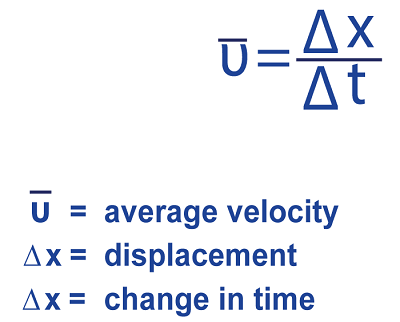

For example, if a car travels 120 miles in three hours, the average velocity of the car can be calculated as 120 miles / 3 hours = 40 miles per hour. This means the car travelled an average of 40 miles per hour over the three hours. Although this is not exact, and we cannot say that car is continuously travelling with this constant average velocity of 40 miles per hour, we get a rough idea of the car's velocity. We can use this data to solve further complex problems.

Velocity and speed are both different terms. Please make sure to distinguish them.

Velocity is often confused with speed, but they are not the same. While velocity (vector quantity) considers both the direction and magnitude of an object's displacement, speed (a scalar quantity) only considers the magnitude of the displacement. Speed has nothing to do with the direction of the object. This means that two objects with the same speed but different directions will have different velocities.

Velocity can be defined as the rate at which a body alters its position in a particular direction. On the other hand, speed is defined as the rate at which a body travels or covers a unit distance (changes in the direction do not matter in this case).

Being a vector quantity, velocity has both a magnitude and a direction. It can be estimated by figuring out an object's displacement over a brief time frame, like a tiny fraction of a second. This measurement is crucial for thoroughly examining how objects move, particularly when the object's velocity changes quickly.

On the other hand, speed is a scalar quantity, meaning it has only magnitude and no direction. It is computed by dividing an object's total distance travelled by its transit duration. Regardless of any variations in velocity that may have occurred during that time, an object's average velocity considers its total displacement and the amount of time required.

One significant difference between velocity and speed is that velocity considers the direction of motion and can be positive, zero, and even negative. In contrast, speed only considers the magnitude of the object's velocity and cannot be negative. For example, an object moving back and forth between two points at the same speed will have zero velocity. Still, its speed will be non-zero since it has covered a distance over time. SI unit of both velocity and speed is the same, that is, m/s.

Average velocity has a lot of uses in the field of motion analysis, particularly in calculating an object's acceleration. The rate at which an object's velocity alters over time is called its acceleration. It is computed by dividing the velocity change by the time it took for that change to occur.

Applications of Average Velocity

Numerous other professions use average velocity, including physics, engineering, and sports. Its significance in the scientific and technical sectors, from sports and GPS technologies to motion analysis, cannot be emphasized. It has contributed to a better knowledge of the world in which we live. The following are some real-world uses for average velocity:

1. Motion Analysis: An average velocity, especially physics, is essential in motion analysis. It helps scientists and engineers to determine how objects move and how they change position over time. In this context, average velocity plays a critical role in calculating the acceleration of an object, which is important in designing and building machines such as cars, aeroplanes, and rockets.
2. Navigation and GPS: Today's world is led by advanced technologies like GPS and Navigation techniques. Average velocity is also used in navigation systems and GPS technology to measure the speed and direction of moving objects. GPS receivers use the average velocity of a moving object to determine its location, direction, and speed accurately. This technology has been useful in various fields, such as aviation, shipping, and transportation. Many modern companies like Uber, Rapido, and Ola are based on Navigation and GPS tools hence, based on the concept of average velocity.
3. Sports: Average velocity is widely used in sports to measure the performance of athletes. For instance, average velocity is used in running to calculate an athlete's speed and determine their expected finishing time in a race. This information is useful for athletes and coaches to evaluate and improve their performance and can perform better in the next match.
4. Traffic Engineering: Average velocity is used in traffic engineering to determine the speed and flow of vehicles on roads and highways. This information is useful in designing and managing transportation systems and reducing traffic congestion. Average velocity can also be used to analyze traffic patterns and to improve traffic safety.
5. Fluid Dynamics: An average velocity is an important tool in fluid dynamics, the study of the movement of fluids. It helps to determine the speed and direction of fluids such as air and water, which is important in designing and building machines such as aeroplanes and ships.

For instance, if a car accelerates from a velocity of 40 miles per hour to 60 miles per hour over 10 seconds, the acceleration of the car can be calculated as (60 miles per hour - 40 miles per hour) / 10 seconds = 2 miles per hour per second. This means the car's velocity increases by 2 miles per hour every second.

Average velocity is mathematically expressed as the ratio of displacement to time, considering the direction of motion. It is an essential concept in physics and engineering, and its formula can be used to calculate the average velocity of an object in motion.

Average velocity = Displacement / Time

Where:

• Displacement (Δx) is the change in the position of an object between its initial and final positions.
• Time (Δt) is the duration for the object to travel that distance.

The displacement and time can be measured in any unit of length and time, respectively, as long as they are consistent. For example, if the displacement is measured in meters and the time in seconds, the average velocity will be expressed in meters per second (m/s).

It is important to note that average velocity considers the direction of motion so that it can be positive or negative depending on the direction of the displacement. If the displacement is in the positive direction, the average velocity will be positive, and if it is in the negative direction, the average velocity will be negative.

The formula for average velocity can also be expressed in terms of the initial and final velocities of an object:

Average velocity = (Initial velocity + Final velocity) / 2

This formula assumes that the object's acceleration is constant, and it is used when the initial and final velocities of the object are known. However, the formula can only be used if the acceleration is constant. The average velocity has to be calculated using the displacement and time shown in the first formula.

Some Solved Examples Based on Average Velocity

Example 1: A train travels a distance of 200 km in 4 hours at a speed of 50 km/h. What is the average velocity of the train?

Solution:

We can use the formula, Average velocity = Displacement / Time.

Displacement = 200 km

Time = 4 hours

Average velocity = 200 km / 4 hours = 50 km/h

Therefore, the average velocity of the train is 50 km/h.

Example 2: A car travels a distance of 120 km in 2 hours. What is the average velocity of the car?

Solution:

Using the formula, Average velocity = Displacement / Time

Displacement = 120 km

Time = 2 hours

Average velocity = 120 km / 2 hours = 60 km/h

Therefore, the average velocity of the car is 60 km/h.

Example 3: A cyclist starts from point A and travels to point B at a speed of 20 km/h, then returns from point B to point A at 10 km/h. If the distance between point A and point B is 60 km, what is the average velocity of the cyclist for the entire journey?

Solution:

To calculate the average velocity of the cyclist, we first need to calculate the total displacement and time taken for the journey.

Displacement = 0 km (since the cyclist ends up at the same point where he started)

Time taken to reach point B = 60 km / 20 km/h = 3 hours

Time taken to return from point B to point A = 60 km / 10 km/h = 6 hours

Total time taken = 3 hours + 6 hours = 9 hours

Using the formula, Average velocity = Displacement / Time

Displacement = 0 km

Time = 9 hours

Average velocity = 0 km / 9 hours = 0 km/h

Therefore, the average velocity of the cyclist for the entire journey is 0 km/h since the cyclist ends up at the same point where he started.

Example 4: A truck travels 120 miles from city A to city B at 60 mph. On the return journey, the truck travels the same distance at 40 mph. What is the average velocity of the truck for the entire journey?

Solution:

To calculate the average velocity of the truck for the entire journey, we first need to calculate the total displacement and the total time taken.

Displacement = 0 miles (since the truck ends up at the same point where it started)

Time taken to travel from city A to city B = 120 miles / 60 mph = 2 hours

Time taken to travel from city B to city A = 120 miles / 40 mph = 3 hours

Total time taken = 2 hours + 3 hours = 5 hours

Using the formula, Average velocity = Displacement / Time

Displacement = 0 miles

Time = 5 hours

Average velocity = 0 miles / 5 hours = 0 mph

Therefore, the average velocity of the truck for the entire journey is 0 mph since the truck ends up at the same point where it started.

Example 5: A sprinter runs 400 meters in 45 seconds. What is the average velocity of the sprinter?

Solution:

Using the formula, Average velocity = Displacement / Time

Displacement = 400 meters

Time = 45 seconds

Average velocity = 400 meters / 45 seconds = 8.89 m/s

Therefore, the average velocity of the sprinter is 8.89 m/s.

Example 6: A cyclist travels 10 miles at a speed of 15 mph and then continues to travel 20 miles at 10 mph. What is the average velocity of the cyclist for the entire journey?

Solution:

To calculate the average velocity of the cyclist for the entire journey, we first need to calculate the total displacement and time taken.

Displacement = 10 miles + 20 miles = 30 miles

Time taken to travel 10 miles = 10 miles / 15 mph = 0.67 hours

Time taken to travel 20 miles = 20 miles / 10 mph = 2 hours

Total time taken = 0.67 hours + 2 hours = 2.67 hours

Using the formula, Average velocity = Displacement / Time

Displacement = 30 miles

Time = 2.67 hours

Average velocity = 30 miles / 2.67 hours = 11.21 mph

Therefore, the average velocity of the cyclist for the entire journey is 11.21 mph.

Conclusion

Average velocity is a fundamental concept in physics that helps to determine the rate at which an object changes its position over time. It is essential in understanding the motion of objects, and it plays a critical role in various scientific and engineering applications. While it may seem simple, it has significant implications for understanding the world.