Polynomial Definition

In mathematics, a 'polynomial' is an expression made up of indeterminates (also known as a variable) and coefficients. It involves the operations of subtraction, addition, multiplication, as well as positive integer factors of the variables. A good example of a polynomial for a single indeterminate x would be x² - 5+7. A good example of 3 indeterminates would be x³ + 3xyz² + yz+1.

Polynomials can be found in numerous sciences and maths. They are, for instance, utilized to create polynomial equations which represent various kinds of issues, from basic word problems to complex scientific ones; they are utilized to define polynomial equations, which are used in various settings from physical and chemical sciences to sociology and economics and are utilized in numerical analysis and calculus to approximate functions. In mathematics that is more advanced, they are utilized to build polynomial rings and algebraic variations, which are fundamental notions of algebra and algebraic geometry.

Etymology

The term "polynomial" combines two distinct roots that are the Greek word 'poly', which translates to "many", and the Latin words "nomen", also known as "name". It comes from the word binomial, substituting its Latin roots bi with poly. It is the sum of many words (many monomials). The word "polynomial" was first employed around the time of the 17th century.

The use of terminology and notation

The x that is present in a polynomial can be known as a variable, also known as an indeterminate. If the polynomial is viewed in terms of an expression, then x is a fixed symbol that has no value (its value is "indeterminate"). But, if one examines the function that is described by the polynomial, it is x that represents the argument for the function, which is why it is referred to as the "variable". Many authors employ these two terms to refer to the same thing.

A polynomial P that is in the indeterminate form x is usually designated as either P or P(x). Informally, the name of Polynomial is P and not P(x). However, the usage of the functional notation P(x) is a result of an era when distinguishing between polynomials as well as the associated function was not clear. Furthermore, it can be useful to describe in one sentence the polynomial as well as its indeterminate. For instance, "let P(x) be a polynomial" is a shorthand form of "let P be a polynomial with an indeterminate x". However, in cases where it's not required to make a point of highlighting the title of an indeterminate, some formulas are simpler and more readable in the event that the name(s) of the indeterminate(s) are not included in every instance in the formula.

The confusion of using two different notations to describe one mathematical object could be resolved informally by looking at the broad meaning of the functional notation used for polynomials. If a refers to a number or variable, a polynomial, or more broadly, any expression, then P(a) is, according to the convention, the outcome of substituting the x in P. This is why the polynomial P defines the function-

Which is the polynomial function associated with P. In most cases, when using this method, one assumes that it is an integer. But it is possible to use it for any domain in which multiplication and addition are defined (that is, any ring). Particularly, if a is a polynomial, then P(a) will also be a polynomial.

If A is the indeterminate x, the image of the x as a result of this function can be described as that of the polynomial P itself (substituting the x with x does make no difference). That is, which formally justifies the existence of two different notations for the same polynomial.

Types of Polynomials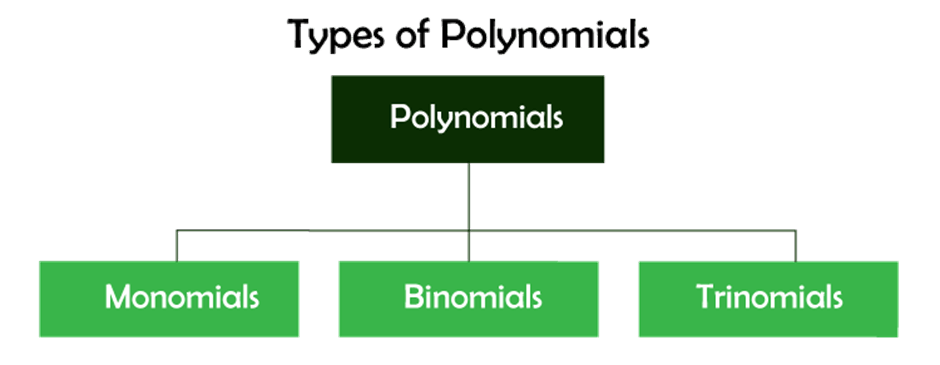

Let's get acquainted with the various forms of polynomials. This will be the basis for further study.

1. Monomials - Monomials are algebraic expressions that contain one term which is why they are called "Mono" mail. Also, it's an expression that includes any number of similar terms. For instance, 2x+5x+10x is a monomial, as when we combine similar terms, we get 17x.
2. Binomials - Binomials are algebraic expressions that have two unlike terms, hence their term "Bi" nominal. For instance, 3x + 4x² can be described as a binomial because it has two terms that are not related. In the same way 10pq + 13p2q is a binominal.
3. Trinomials- Trinomials are algebraic expressions that have three unlike terms, hence their term "Tri" nominal. For example, 3x + 5x² + 6x³ is trinomial. This is because of the existence of three terms that are not related, that is, 3x, 5x² as well as 6x³.

There is another type of polynomial, known as a "zero" polynomial. In this kind, the sum of every coefficient equals zero. For instance, 0x² + 0x - 0.

Degree of a Polynomial

It is the greatest of all the powers or exponents over the many terms within the mathematical expression.

Example: Find the degree of 7x + 5.

In the above example, the first term is 7x, while the second one is 5. Let's determine the exponent of each term. The exponent for the initial term, 7x, is 1, while for the second term, 5, the exponent is zero. Because the exponent with the highest value of 7x is 1, the degree of 7x + 5 is also 1.