Simple Harmonic Motion Definition

Introduction

Simple harmonic motion is a fundamental concept in physics and engineering that refers to the repetitive motion of an object back and forth around an equilibrium point. This motion is characterised by a specific pattern of acceleration, velocity, and displacement that can be described using mathematical equations.

The motion of the object in simple harmonic motion can be described using a sine or cosine function, depending on the direction of the motion. This function represents the displacement of the object from its equilibrium point as a function of time. The frequency of the motion, which is the number of complete cycles per unit time, is determined by the properties of the object and the forces acting on it.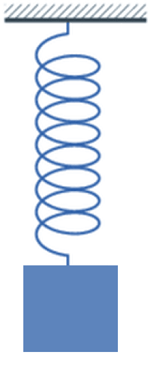

One of the key features of simple harmonic motion is that the acceleration of the object is directly proportional to its displacement from the equilibrium point but in the opposite direction. This means that the object experiences the greatest acceleration when it is furthest from the equilibrium point, and the least acceleration when it is closest to the equilibrium point. This relationship is described by Hooke's Law, which states that the force required to displace an object from its equilibrium point is proportional to the displacement.

The velocity of the object in simple harmonic motion also follows a specific pattern. As the object moves away from the equilibrium point, its velocity decreases to zero at the point of maximum displacement and then increases again as it moves back towards the equilibrium point. At the equilibrium point, the velocity is at its maximum.

Concepts of Simple Harmonic Motion

Simple harmonic motion is a type of motion that is characterized by a specific pattern of acceleration, velocity, and displacement. There are several different concepts that are important to understand when studying simple harmonic motion.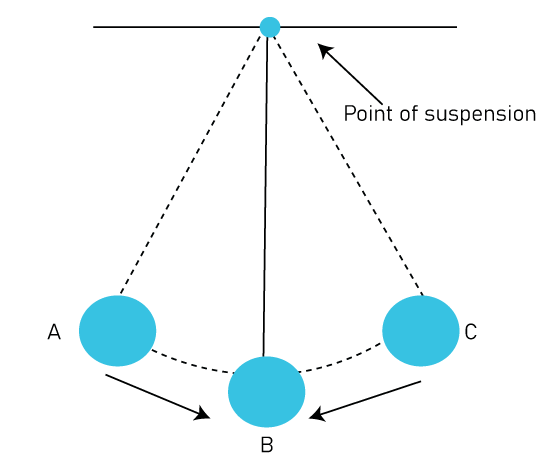

Equilibrium point: The equilibrium point is the position at which an object experiences zero net force and remains at rest. In simple harmonic motion, the object is initially placed at the equilibrium point and then disturbed from that position, causing it to oscillate back and forth around the equilibrium point.

Amplitude: The amplitude of the motion is the maximum displacement of the object from its equilibrium point. This value determines the total distance that the object oscillates back and forth during the motion.

Period: The period of motion is the time it takes for the object to complete one full oscillation cycle. The period is determined by the frequency of the motion, which is the number of oscillation cycles per unit time.

Frequency: The frequency of the motion is the number of complete oscillation cycles per unit of time. It is inversely proportional to the period of the motion. The frequency is determined by the properties of the object and the forces acting on it.

Hooke's Law: Hooke's Law is a fundamental law of physics that states that the force required to displace an object from its equilibrium point is proportional to the displacement. This law is important in understanding the relationship between the acceleration of the object and its displacement from the equilibrium point.

Phase: The phase of the motion describes the position of the object within the oscillation cycle. It is measured as the fraction of the period that has elapsed since the object last passed through the equilibrium point.

Velocity: The velocity of the object in simple harmonic motion follows a specific pattern. As the object moves away from the equilibrium point, its velocity decreases to zero at the point of maximum displacement and then increases again as it moves back towards the equilibrium point. At the equilibrium point, the velocity is at its maximum.

Acceleration: The acceleration of the object in simple harmonic motion is directly proportional to its displacement from the equilibrium point, but in the opposite direction. This means that the object experiences the greatest acceleration when it is furthest from the equilibrium point, and the least acceleration when it is closest to the equilibrium point.

Examples

Here are some examples of simple harmonic motion:

• Pendulum: A pendulum is a classic example of simple harmonic motion. The motion of the pendulum is governed by the force of gravity acting on a suspended weight. As the weight swings back and forth, it exhibits a specific pattern of acceleration, velocity, and displacement that can be described using the equations of simple harmonic motion.
• Spring-mass system: A spring-mass system is another common example of simple harmonic motion. In this system, a mass is attached to a spring and set into motion. As the spring is compressed and extended, the mass oscillates back and forth around the equilibrium point. The motion of the mass can be described using the equations of simple harmonic motion.
• Guitar string: The vibration of a guitar string is an example of simple harmonic motion. When a guitar string is plucked, it vibrates back and forth, producing a sound wave. The frequency of the vibration determines the pitch of the sound produced. The motion of the string can be described using the equations of simple harmonic motion.
• Torsion pendulum: A torsion pendulum is a type of pendulum that oscillates in a circular motion. It consists of a suspended rod or wire that is twisted and released. As the wire untwists, it exhibits a specific pattern of acceleration, velocity, and displacement that can be described using the equations of simple harmonic motion.
• Mass attached to a rotating disk: When a mass is attached to a rotating disk and set into motion, it exhibits simple harmonic motion. As the disk rotates, the mass oscillates back and forth around the circumference of the disk. The motion of the mass can be described using the equations of simple harmonic motion.

These are just a few examples of simple harmonic motion. The principles of simple harmonic motion are found in many different systems and phenomena, from the motion of atoms and molecules to the motion of waves in the ocean. Understanding these principles is important in being able to analyze and predict the behavior of systems exhibiting simple harmonic motion.

Calculation of Simple Harmonic Motion

The calculation of simple harmonic motion involves determining the period, frequency, amplitude, and displacement of the motion. The period is the time taken for one complete cycle of the motion, and is given by the formula:

Where T is the period, m is the mass of the object, and k is the spring constant of the spring. The frequency of the motion, which is the number of cycles per second, is given by:

where f is the frequency.

The amplitude of the motion is the maximum displacement from the equilibrium position and can be determined by measuring the maximum displacement of the mass from the rest position. The displacement of the mass from the equilibrium position at any time t is given by the equation:

where x is the displacement, A is the amplitude, ω is the angular frequency, t is the time, and φ is the phase constant.

The angular frequency ω is given by:

where f is the frequency.

The phase constant φ represents the initial displacement of the mass at time t=0. It can be determined by measuring the position of the mass at a known time and substituting the values into the equation.

Types of Simple Harmonic Motion

There are three types of simple harmonic motion, which are described below.

Linear simple harmonic motion: In linear simple harmonic motion, the object moves back and forth along a straight line. This type of motion is seen in pendulums, mass-spring systems, and certain types of waves. In a mass-spring system, for example, the mass oscillates back and forth on a horizontal surface while connected to a spring. The force acting on the mass is proportional to its displacement from its equilibrium position, which results in a sinusoidal motion.

Angular simple harmonic motion: In angular simple harmonic motion, the object rotates back and forth around a fixed point. This type of motion is seen in objects such as a torsion pendulum, where the torsion wire acts as the restoring force, and in the motion of a simple pendulum. The motion of a simple pendulum can be described as an angular simple harmonic motion if the amplitude of the motion is small.

Damped simple harmonic motion: Damped simple harmonic motion is a type of simple harmonic motion where the amplitude of the oscillation decreases over time due to the presence of external forces such as friction. This type of motion is seen in many real-world systems, such as a swinging door, a car suspension system, and a child's swing. The amplitude of the oscillation decreases exponentially with time, and the frequency of the motion remains constant.