Complementary Angles Definition

These are created when two angles are combined, resulting in a 90° angle. The two angles are also considered to complement one another.

Complementary angles in geometry are a pair of angles where the right angle is formed by combining any other angles. The values of the next pair of angles, such as 60° and 30°, 40°, and 50°, etc., whose total is 90°.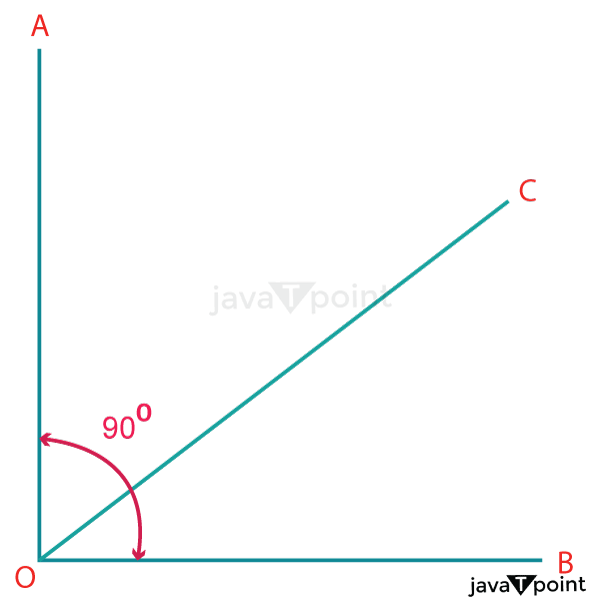

In this case, the angles of AOC and BOC are complementary.

Explanation of the Complementing Angles Procedure

You only need to use their angle values to determine if angles are complementary. Angle values must match the proper angle of 90° if the complementary angles' right angle is the same as the total of the two angles. The pair of angles are referred to as complementary if the angle's total value is 90° or more. In the illustration, two angles that make a right angle may be shown to have complementary angles.

Definition of Complementary Angles

The combination of two angles, known as complementary angles, is said to have a sum of values that is precisely 90°. The two angles' values combine to create a right angle with a 90° angle. Two angles are complementary if the total of them equals 90 degrees. It is an essential standard for complementary angles. The total of the angles AOC and BOC in the earlier figure, which has values that vary from 30° to 60°, 40° to 50°, 65° to 25°, 48° to 42°, and so on, will equal 90°. Complements to one another refer to the angles that make up a pair of complementary angles.

Various Types of Complementary Angles

As mentioned before, complementary angles refer to two angles that, when added together, result in a right angle. A pair of angles that are opposed to one another are referred to as complementary angles. The two complementing angle types listed below are described in further depth:

1. Adjacent Complementary Angles
2. Non- adjacent Complementary Angles

1. Adjacent Complementary Angles

A pair of angles with the same vertex and arm is called "adjacent complementary angles." The illustration below shows the angles AOC and BOC, which are nearby complementary angles that share the same arm and vertex.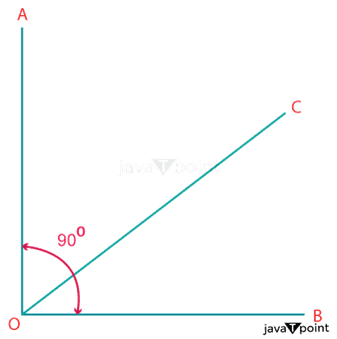

2. Non-Adjacent Complementary Angles

Non-adjacent complementary angles are two complementary angles that are not exactly next to one another. The sum of the two angles must always equal 90° even if it lacks a standard arm and vertex. Below is a diagram that displays the non-adjacent complementary angles.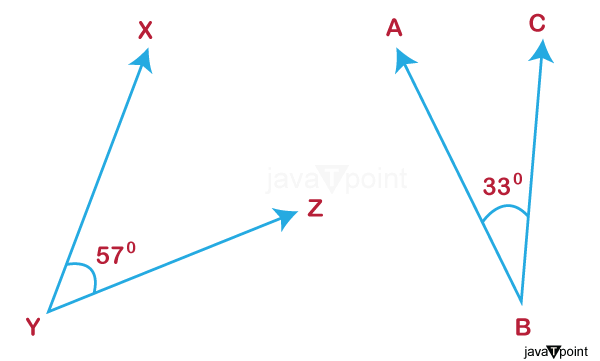

As their total is 90° in the preceding illustration, the angles XYZ and ABC are complementary.

Angles that are Complementary and Supplementary

Complementary and supplementary angles are determined by adding two angles together. When two angles are added together, they comprise complementary angles, 90°, and supplementary angles, which are 180°. Angle measurement is the foundation of all of these angles. The two angles that complement one another and have values of 180° are referred to as supplementary angles-a straight line results when the two extra angles are joined. The following illustration explains complementary and supplementary angles: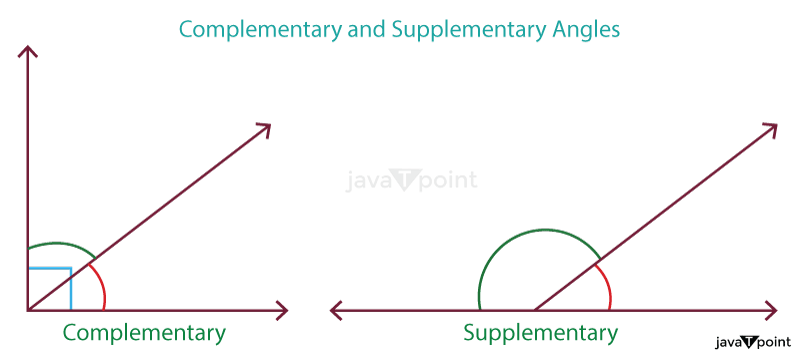

The accompanying illustration shows how complementary and supplementary angles differ from one another. They are typically in opposition to one another.

Examples of Complementary Angles

The angles that add up to a right angle, or a 90° angle, are the complementary angles. The complements of one another are the complementary pairs of complementary angles whose values equal 90°. The complementary angles might range from 30° and 60° to 40° and 50° to 55° and 35°, and so on. Below are some illustrations of complementary angles.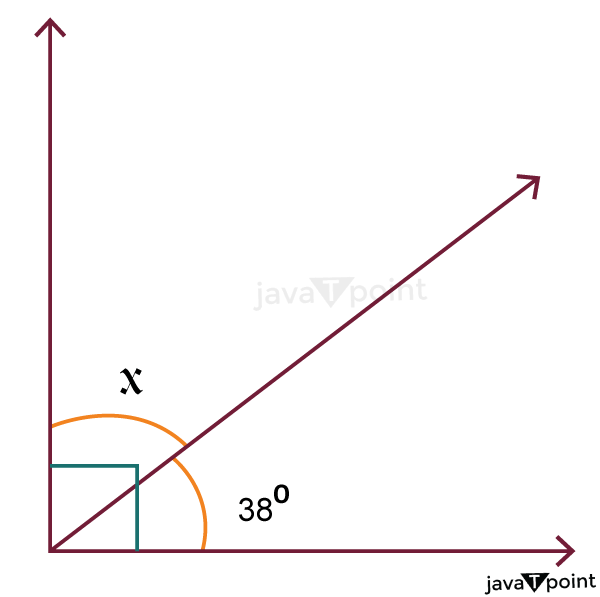

We must determine the angle x's value in the following graphic as one angle is specified as 38° and another is absent.

We are aware that two complementary angles added together equal 90°.

then, x + 38° = 90°, x = 52°

Angle x has a value of 52°.

Using the characteristics of angles, you can also determine the values of other angles.

How to Identify Complementary angles

How do you discover a complementary angle if you are given a 70° angle and instructed to do so?

Simply subtraction 70° from 90° gives the measure of an angle complementary to a 70° angle.

90°−70°=20°

The 20° angle is the one that is missing.

A right triangle may be used to make complementary angles quickly. To draw a straight line across the triangle, begin at the right angle vertex. Whenever you create a line, you also create two angles that complement each other.

Learn about the Differences Between Complementary and Supplementary Angles

When the sum of two angles equals 90 degrees, they are considered to be complementary. When an angle is 50 degrees, its complement measures 40 degrees.

Complementary angles refer to a pair of angles that, when added together, result in a sum greater than 180 degrees. The term "straight angle" refers to the combination of supplementary angles. A straight line will result if you add arrows to the ends of the right angle. When you have an angle that measures 100 degrees, its supplementary angle can only measure 80 degrees.