Reflex Angle Definition

Angles play a crucial role in the field of geometry, and are categorized into various types, including acute, obtuse, right, and reflex angles. However, reflex angles often receive less attention or are misunderstood compared to the other types of angles. Reflex angles are angles that measure greater than 180 degrees but less than 360 degrees. This article aims to provide a comprehensive understanding of reflex angles by discussing their properties, measurement, applications, types, and examples. Additionally, we will offer exercises to help readers test their knowledge on this important mathematical concept.

What is a Reflex Angle?

A reflex angle is an angle that measures more than 180 degrees but less than 360 degrees. To understand this better, let's take the example of a spinning top. Imagine you spin a top on a flat surface, and you draw a straight line on the surface to represent the starting position of the top. As the top spins, it moves away from the starting position and continues to spin until it completes a full circle. Now, imagine that the top continues to spin even after it completes a full circle and moves further away from the starting position. The angle formed between the starting position and the direction the top is spinning at this point is a reflex angle. This angle measures more than 180 degrees but less than 360 degrees.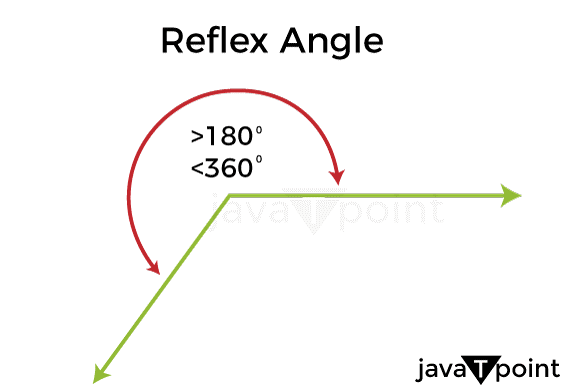

Real Life Example of Reflex Angles

• When a gymnast completes a flip in the air and lands back on the ground, the angle between the direction of the jump and the landing point is a reflex angle.
• The angle between the blades of a windmill and the direction of the wind when it is moving faster than the wind speed is a reflex angle.
• In a kaleidoscope, the angle formed between the two mirrors where they meet is a reflex angle.
• In a car race, when a driver takes a turn at high speed and completes a full circle, the angle formed between the direction of the car's motion and the starting position is a reflex angle.
• When a beam of light reflects off a mirror and travels in a direction opposite to the incident ray, the angle between the incident ray and the reflected ray is a reflex angle.
• When the minute hand of a clock moves past the 6 o'clock mark and continues to move in a clockwise direction, it forms a reflex angle between the starting position and the direction the hand is pointing. This angle measures more than 180 degrees but less than 360 degrees.

Properties of Reflex Angles

• A reflex angle measures more than 180 degrees but less than 360 degrees.
• The sum of a reflex angle and its corresponding acute angle is 360 degrees. For example, if a reflex angle measures 220 degrees, its corresponding acute angle measures 140 degrees because 220 + 140 = 360.
• The interior angles of a polygon, when added together, will always equal a multiple of 180 degrees. If a polygon has a reflex angle, the sum of its interior angles will be greater than 180 degrees but less than 360 degrees.
• The vertex of a reflex angle is located outside of the circle that the angle is a part of.
• A reflex angle can be bisected, or divided into two equal parts, using the same procedure as with an acute or obtuse angle.
• The arms of a reflex angle can be located on the same side of the line that forms the angle.

Applications of Reflex Angles

• Surveying: In surveying, reflex angles are used to measure the angles between two intersecting lines that are greater than 180 degrees but less than 360 degrees.
• Road Design: In designing roads, reflex angles can be used to measure the curvature of a road or a bend. The angle formed between the tangent of a curve and a straight line extending from it is a reflex angle.
• Architecture: In architecture and construction, reflex angles are used to design complex geometric shapes and angles that are required for aesthetic and structural reasons.
• Art and Design: Reflex angles can be used in art and design to create visually appealing and complex geometric patterns, shapes, and angles.
• Games: In games such as billiards and pool, when a ball bounces off the wall and returns to the playing area, the angle between the direction of the ball's motion and the wall is a reflex angle.

How to Measure a Reflex Angle

To measure a reflex angle, we need to use a protractor, which is a tool specifically designed to measure angles. The steeps that we need to follow to measure a reflex angles are:

1. Place the protractor with the center hole over the vertex (corner) of the angle.
2. Align the baseline of the protractor with one of the sides of the angle.
3. Read the angle measurement where the other side of the angle intersects the protractor scale.

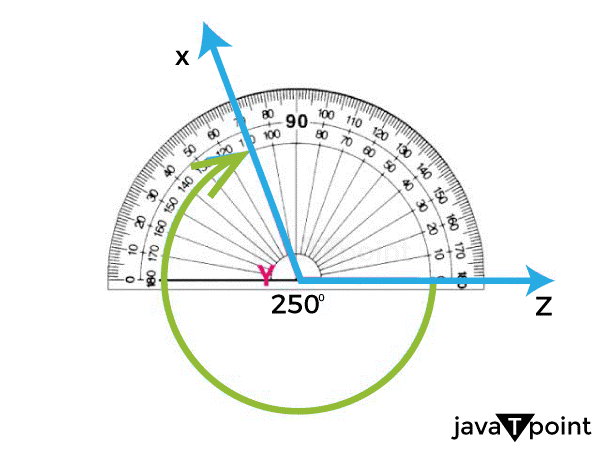
Let us take an example, to find the angle of a corner in a room, we need to follow following steps:

1. Place the center of the protractor at the corner of the room.
2. Align one of the sides of the protractor with one of the walls.
3. Read the measurement of the angle where the other wall intersects the protractor scale.

It is of paramount importance to note that a reflex angle is typically not used in your everyday measurements. This is because they are of greater measure than a straight angle (180 degrees) and can be difficult to visualize. In most cases, measuring acute angles (less than 90 degrees) or obtuse angles (greater than 90 degrees) is sufficient.

Types of Reflex Angles

Similar to the standard angles, reflex angles are also classified into three different types, which are:

1. Acute reflex angles: These are angles that are greater than 180 degrees but less than 270 degrees. These angles are formed by adding an acute angle to a straight angle. An example of an acute reflex angle is an angle that measures 220 degrees.
2. Right reflex angles: Theseare angles that measure exactly 270 degrees. These angles are formed by adding a right angle to a straight angle. An example of a right reflex angle is an angle that measures 270 degrees, which is formed by adding a 90-degree right angle to a 180-degree straight angle.
3. Obtuse reflex angles: These are angles that measure greater than 270 degrees but less than 360 degrees. These angles are formed by adding an obtuse angle to a straight angle. An example of an obtuse reflex angle is an angle that measures 320 degrees.

Some Questions on Reflex Angles

To better understand the concept of reflex angles, let us solve some practice problems of varying difficulty.

Question- 1 Find the measure of the reflex angle formed by a clock's hour and minute hand at 4:45.

Answer: The minute hand is at the 9 position while the hour hand is at 4. The angle formed by the hour hand is 430 = 120 degrees. The angle formed by the minute hand is 45/60360 = 270 degrees. The reflex angle formed is the difference between the two, which is 270 - 120 = 150 degrees.

Question-2 Find the measure of the reflex angle formed by two lines that intersect each other, where the acute angles formed are 45 and 60 degrees respectively.

Answer: The two acute angles formed by the intersecting lines add up to 45 + 60 = 105 degrees. Therefore, the reflex angle formed is 360 - 105 = 255 degrees.

Question-3 In a regular octagon, what is the measure of the reflex angle formed by two adjacent vertices?

Answer: Each interior angle of a regular octagon measures 135 degrees. The acute angle formed by two adjacent vertices of the octagon is half of this, or 67.5 degrees. Therefore, the reflex angle formed by these two adjacent vertices is 360 - 2(67.5) = 225 degrees.

Question-4 In a triangle, one angle measures 135 degrees and another angle measures 60 degrees. What is the measure of the reflex angle formed by the remaining angle?

Answer: The sum of the two known angles is 135 + 60 = 195 degrees. Therefore, the reflex angle formed by the remaining angle is 360 - 195 = 165 degrees.

Question-5 In a parallelogram, one angle measures 110 degrees. What is the measure of the reflex angle formed by the adjacent angle?

Answer: Since opposite angles in a parallelogram are congruent, the adjacent angle also measures 110 degrees. Therefore, the reflex angle formed by the adjacent angle is 360 - 110 = 250 degrees.