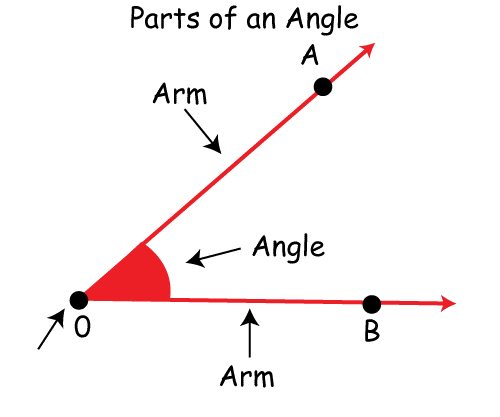
Complete Angle Definition

A geometric shape known as an angle is created when two rays meet at a location known as the vertex. The degree of rotation between the two rays, typically stated in degrees, radians, or gradians, determines the measurement of an angle. Angles are crucial in geometry and are used to define the connection between two lines or planes and quantify the size of forms and objects. Angles are a useful tool for comprehending and examining the characteristics of geometric figures in this way.

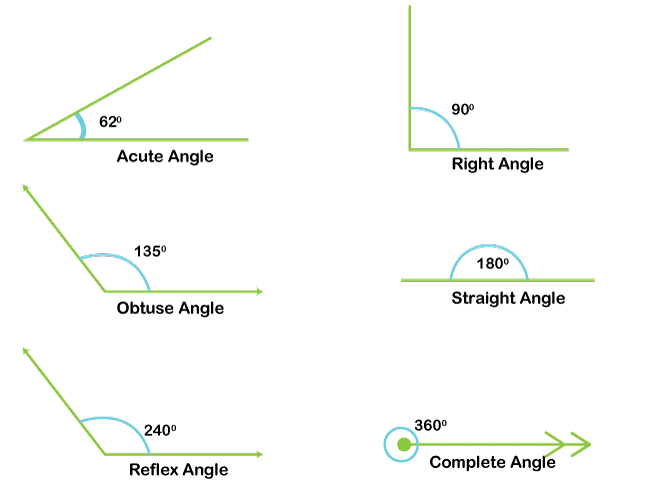
Types of Angles

Depending on how they are measured and where they are, there are many angles in geometry. The following are some of the most typical angles:

Acute Angle

An acute angle is smaller than 90 degrees in length.

Right Angle

A right angle is exactly 90 degrees in angle measurement. In schematics, it is frequently represented by a little square.

Obtuse Angle

An angle greater than 90 but less than 180 degrees is considered obtuse.

Straight Angle

A straight angle is 180 degrees in length. A straight line divides a plane into two halves.

Reflex Angle

An angle greater than 180 degrees but less than 360 degrees is called a reflex angle.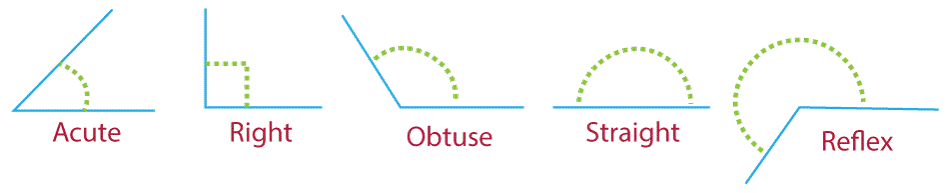

Complementary Angles

Angles that are complimentary have a combined angle that is exactly 90 degrees.

Supplementary Angles

Angles supplementary to one another are those whose sum is exactly 180 degrees.

Vertical Angles

Two non-adjacent angles created by the intersection of two lines are called vertical angles. They always have the same measure and are congruent.

Comprehending the many kinds of angles is crucial because of their unique qualities and relationships, which may be used to solve issues and analyze geometrical objects.

Complete Angle Definition

An angle that measures exactly 360 degrees is said to be a full angle. It comprises two rays extending in opposing directions and completely encircling the vertex, their shared terminal. In other words, a full revolution around a point constitutes a complete angle. In schematics, it is frequently represented by a little circle.

Complete angles have several significant characteristics. First, a Complete angle is any angle that is a multiple of 360 degrees (for example, 720 degrees, 1080 degrees, etc.). In addition, any two angles that sum to 360 degrees are complementary, which enables them to be joined to create a Complete angle. Lastly, Complete angles serve as a standard against measuring other angles. For instance, a half-rotation (180 degrees) is frequently used as a standard for gauging other angles because it represents one-half of a whole revolution.

Complete angles are crucial in several disciplines, including physics, engineering, and mathematics. They are used to analyze the motion of spinning objects and systems and to define the characteristics of circles, spheres, and other curved objects.

Complete Angles Examples

Examples of Complete angles:

• The hour hand on a clock completes a full rotation, or 360 degrees, every 12 hours, comparable to a whole rotation.
• The Earth spins 360 degrees around its axis every 24 hours, completing one full rotation.
• When a car or bicycle wheel travels the equivalent of its circumference, which is twice the wheel's radius, it has completed one full rotation. A 360-degree rotation would be the same as this.
  
• A complete rotation of a planet around the sun: The time it takes for a planet in our solar system to do one full rotation around the sun varies depending on the planet. For instance, Earth rotates 360 degrees in 365.24 days or one full revolution.
• A full rotation of 360 degrees around a vertical axis is frequently required for a complete turn or spin in gymnastics or dance.

These are only a few instances in which Complete angles are employed. Generally, a complete angle of 360 degrees can represent any situation involving a full rotation or revolution around a given point or axis.

Completion Angles Characteristics

Complete angles have several important qualities, including:

• A whole angle is 360 degrees in length.
• A full angle is any angle that is a multiple of 360 degrees.
• Any complementary angles that sum to 360 degrees can be combined to create a Complete angle.
• A complete angle is the total of all other angles in a polygon. For instance, the total angle in a triangle is 180 degrees or one-half of a whole angle.
• By deducting or adding multiples of 360 degrees, every angle more than 360 degrees can be transformed into an equivalent angle between 0 and 360 degrees.
• Additional angles can be measured using a complete angle as a standard. For instance, a half-rotation (180 degrees) is frequently used as a standard for gauging other angles because it represents one-half of a whole revolution.
• Any angle that is a multiple of 360 degrees has sine, cosine, and tangent values that are identical to their corresponding angles between 0 and 360 degrees. This is because these trigonometric functions are periodic.

Understanding full angles' properties is crucial to analyzing and resolving issues involving polygons, circles, and other geometric forms. Trigonometry, a field of mathematics that studies the connections between angles and sides of triangles, relies heavily on full angles and their characteristics.

Applications of Complete Angles

Complete angles have several practical uses, including the following:

Navigation

To ascertain the direction of travel and calculate distances between sites, complete angles are employed in navigation, particularly in the aviation and maritime industries. Spherical coordinates, which require the determination of angles in three dimensions, are also used in navigation.

Astronomy

In astronomy, complete angles explain how celestial bodies are positioned around one another and to the observer. When measuring angles in the sky, astronomers employ a coordinate system based on the celestial equator and poles.

Engineering

To construct and analyse rotating structures like gears, turbines, and motors, Complete angles are utilized in engineering. Engineers use calculus and trigonometry to determine the forces and torques involved in spinning objects' motion.

Photography and Videography

Complete angles are used in both mediums to manage the arrangement and framing of photos and videos. For instance, using complete-angle and fisheye lenses to capture a broad field of view or a skewed perspective can provide dramatic results.

Sports

Sports involving rotational motion, such as gymnastics, diving, and figure skating, use whole angles. Athletes apply the laws of physics and biomechanics to execute complex actions and improve their performance.

Gaming

Video games employ complete angles to manage virtual characters' and objects' movement and rotation. Video game makers use mathematical models and algorithms to replicate realistic physics and motion.

These are only a few instances of Complete angles employed in actual situations. In general, angles and their characteristics can be used to explain any scenario involving rotation, direction, or location.

How to Measure a Complete Angle

You must complete a full rotation around a given point or axis to measure an Complete angle. You can do this by physically rotating an object or body, using a protractor or other measurement device, or both.

If you're using a protractor, place the baseline along one of the angle's sides and the protractor's centre at the angle's vertex. When the other side of the angle intersects the scale on the protractor, read the measurement there. The measurement is 360 degrees if the angle is Complete.

Mark the starting point and complete a full revolution around the fixed point or axis if you physically rotate an item or your body. Then, using a protractor or other measuring device, determine the angle between the starting position and the ending point. Again, the measurement will be 360 degrees if the angle is Complete.

Complete angles are a particular instance and are uncommon in real-world circumstances; it is vital to remember this. It is possible to measure acute, obtuse, and right angles, which comprise the majority of angles we encounter, using the same methods as complete angles.

The Relationship Between Revolutions and Complete Angles

Since both ideas entail a complete rotation around a fixed point or axis, complete angles and revolutions are directly related.

One entire revolution equals one complete angle, which has a length of 360 degrees. In other words, a complete revolution measures how often an item or system has done a full rotation, and a complete-angle measure how much an object or system has rotated around a fixed point or axis.

This connection is frequently employed in physics, engineering, and other rotational motion disciplines. For instance, the number of revolutions per unit of time is frequently employed to measure an item's rotation rate when determining its angular velocity.

It is also important to note that circular motion, a key idea in physics, is intimately related to the ideas of full angles and revolutions. When an object moves in a circular path around a fixed point or axis, the distance travelled along the path is proportional to the angle by which the object rotates.

Using Complete Angles in Calculus and Trigonometry

Complete angles are used in calculus to investigate periodic functions, which are functions whose values recur throughout time. Periodic functions can simulate various physical events, including waves and oscillations. To solve equations and make predictions, periodic function analysis examines their characteristics, such as amplitude, period, and phase shift.

Overall, the knowledge of the behaviour of circular functions and periodic phenomena, as well as the application of these ideas to real-world issues in physics, engineering, and other disciplines, depends on the usage of Complete angles in trigonometry and calculus.

Role of Complete Angles in 3D Geometry

Complete angles function in three-dimensional geometry and spherical coordinates.

Spherical coordinates are a system of coordinates used to describe points in three-dimensional space, and 3D geometry heavily relies on complete angles.

The distance from the origin (r), the angle between the positive z-axis and the radius vector (), and the angle between the positive x-axis and the projection of the radius vector onto the xy-plane () are the three values used to define a point in spherical coordinates.

The angle measures the full rotation of the z-axis. Hence it is a complete angle. As a result, any two values that differ by a multiple of 2 represent the same location in space, and the values are periodic with a period of 2.

When studying spherical symmetry, complete angles play a crucial role in spherical coordinates, which is the quality of symmetric objects around an axis or fixed point. Spherical coordinates are frequently employed to explain the properties and behavior of many physical systems, including planets, stars, and molecules.

Complete angles are also employed in 3D geometry to describe how things rotate in three dimensions. An angle of rotation, which can range from 0 to 360 degrees (or 0 to 2 radians) and is measured in degrees or radians, represents the rotation of a three-dimensional object around a fixed axis. A 360-degree (or 2 radians) angle represents the full revolution of the axis.

Common Misunderstandings and Mistakes about Complete Angles

Complete angles are the subject of frequent misunderstandings and mistakes, which can cause confusion and error in science and maths. Here are a few of the most typical misunderstandings:

• One typical misunderstanding is confounding Complete angles with other angles, such as reflex or straight angles. While these and Complete angles are related, they are not the same.
• Another typical mistake is considering full angles as though they were measured in other units, such as minutes or seconds, instead of remembering that they are measured in degrees or radians.
• Complete angles have a period of 360 degrees (or 2 radians), which means that any two angles that differ by a multiple of 360 degrees (or 2 radians) indicate the same angle. This is a mistaken interpretation of the periodicity of complete angles. It's crucial to remember that this periodicity only applies to Complete angles, not other angles.
• Using the words "rotation" and "revolution" interchangeably, Although they both entail the movement of an item around a fixed point or axis, revolutions, and rotations are distinct ideas. While a rotation can refer to any rotation angle, not always a Complete angle, a revolution refers to a full turn around a fixed point or axis.

The Importance of Complete Angles in History and Culture

Complete angle's historical and cultural relevance can be shown in several ways:

Ancient Astronomy and Astrology

Numerous ancient civilizations, including the Egyptians, Babylonians, and Greeks, acquired a thorough understanding of the motions of celestial objects. They used Complete angles to comprehend and predict astronomical occurrences, such as the motions of the sun, moon, and stars. This information served as the foundation for early astrology and astronomy.

Calendars and Timekeeping

The concept of entire angles is strongly tied to dividing time into days, hours, and minutes. Ancient civilizations created calendars using astronomical observations, such as the movement of the sun and stars. The cyclical course of the sun was divided into 365 or 360 segments using the whole angle of 360 degrees, which served as the foundation for calendars and timekeeping systems.

Exploration and Navigation

Complete angles have been essential for both throughout history. Explorers and navigators used astronomical observations, such as the sun, moon, and star positions, to pinpoint their locations and plan their trips. Understanding Complete angles aided their comprehension of the Earth's rotation and how it affected heavenly bodies.

Cultural Symbolism

Complete angles and full rotations have symbolic meanings in many different civilizations. Complete angles are related to wholeness, completion, and cycles. It frequently serves as a metaphor for harmony, togetherness, and limitless potential. Complete angles can symbolize spiritual or cosmic features in artwork, religious symbols, and cultural rites.

Development of Mathematics and Science

The idea of Complete angles has been crucial to advancing mathematics and science. Geometry, calculus, and trigonometry all rely largely on comprehending and computing Complete angles. They lay the groundwork for comprehending wave phenomena, circular motion, and numerous other scientific and mathematical concepts. We can better comprehend Complete Angle's role in influencing human knowledge, exploration, and understanding of the universe if we know its historical and cultural significance.