Corresponding Angles Definition

Corresponding angles are an important concept that we study early on while studying geometry. What are they? Let's suppose two straight lines that never cross each other, such as railway tracks, in order to find the solution to this issue. These two lines are referred to as parallel lines. Now see a bridge-like third line passing over them. A transversal line is the name given to the third line. The intersection of the two parallel lines and the transversal line results in four angles. Corresponding angles are pairs of these angles that are on opposite sides of the transversal line and in the same position on each of the parallel lines we name them such since they correspond to each other.

Understanding the concept of corresponding angles is important in geometry. They help us solve many problems and help us understand more difficult geometrical concepts. Let us delve deeper into corresponding angles and explore their properties and uses.

What Are the Corresponding Angles?

Corresponding angles can be thought of as mirror reflections of one another that are situated on either side of a transversal that joins two parallel lines. When two parallel lines are intersected by a third line, known as a transversal, the resulting angles are said to be in correspondence, or in matching positions.

The respective angles are situated in corresponding locations, that is, one angle is on one side of the transversal and the other angle is on the opposite side of the transversal and in the same position with respect to the parallel lines. In other words, on two separate intersecting lines, corresponding angles are situated in the same relative location. Let's look at an example to help you better comprehend the idea of comparable angles.

Consider line AB and line CD, two parallel lines that are intersected by line GH, a transversal line, as illustrated in the diagram below.

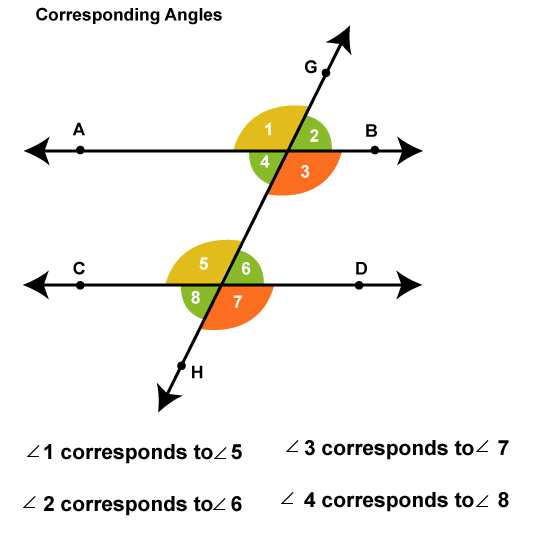
The parallel lines in the diagram are lines AB and CD, while line GH is the transversal. The intersection of the parallel lines, which are marked below, creates eight angles.

• Angle 1: The top left angle created by the transversal GH and the intersection with Line AB.
• Angle 2: The top right angle created by the transversal GH and the intersection with Line AB.
• Angle 3: The bottom right angle created by the transversal GH and the intersection with Line AB.
• Angle 4: The bottom left angle created by the transversal GH and the intersection with the Line AB
• Angle 5: The top left angle created by the transversal GH and the intersection with the Line CD
• Angle 6: The top right angle created by the transversal GH and the intersection with the Line CD
• Angle 7: The bottom right angle created by the transversal GH and the intersection with the Line CD
• Angle 8: The bottom left angle created by the transversal GH and the intersection with the Line CD

Let's concentrate on the corresponding angles right now. As previously mentioned, corresponding angles are the pairs of angles that are located at each intersection of the parallel and transversal lines in the same relative place. The equivalent angles in the aforementioned scenario are:

• Angle 1 and Angle 5 are a pair of comparable angles since they are located at their respective points of intersection in the same relative location (top-left).
• Angle 2 and Angle 6 are a pair of comparable angles since they are located at their respective points of intersection in the same relative location (top-right).
• Angle 3 and Angle 7 are a pair of comparable angles since they are located at their respective points of intersection in the same relative location (bottom-right).
• Angle 4 and Angle 8 are a pair of comparable angles since they are located at their respective points of intersection in the same relative location (bottom-left).

Properties of Corresponding Angles

Now that we have learnt about the corresponding angles, it is important to expand our knowledge by exploring more deeply into their properties. By doing so, we can gain a more comprehensive understanding of their behaviour and importance in various mathematical applications. Some important properties of corresponding angles are discussed below:

1. Corresponding angles are congruent: As we know, when two parallel lines are crossed by a third line (called a transversal), the angles that are in the same position on each line are called corresponding angles. If the two lines are parallel, then the corresponding angles will have the same measurement. So, if one corresponding angle is, for example, 50 degrees, then all other corresponding angles will also be 50 degrees. This is called the Corresponding Angles Postulate.
2. Corresponding angles are in the same position: Corresponding angles are angles that are in the same position on two different lines crossed by a third line. For example, let us imagine a letter "Z" made by two straight lines with another straight line crossing through it, the angles that are in the same position (like the top-left angle and bottom-right angle) are corresponding angles. If one of those angles is in a certain position relative to the third line (the one crossing through the "Z"), then its corresponding angle will be in the same position on the other line.
3. Corresponding angles are formed by alternate interior angles: Alternate interior angles are a type of angle that is formed on opposite sides of the transversal (the third line) and inside the two parallel lines. And if these alternate interior angles are in the same position at each intersection, they are called corresponding angles.
4. Corresponding angles can be used to prove that lines are parallel: If we have two lines and a transversal, and we notice that certain pairs of angles that are in the same relative position are congruent (meaning they have the same angle measurement), then we can say that the two lines are parallel. This is called the Corresponding Angles Converse. So, if we have a pair of parallel lines and a transversal crossing them, the corresponding angles will always be congruent.

By studying their properties, we can conclude that corresponding angles play a significant role in geometry, particularly when dealing with parallel lines and transversals. By understanding the properties of corresponding angles, we can not only identify congruent angles but also prove the parallelism of lines. Therefore, it is important to have a solid grasp of this concept to solve various mathematical problems effectively.

Uses of Corresponding Angles

Corresponding angles are important because we use them for several practical applications in the real world. In this section, we will explore some of the most common uses of corresponding angles.

1. Navigation: Corresponding angles are used in navigation systems such as compasses and maps. In order to find your way from one location to another, you need to be able to determine the angle between your starting point and your destination. Corresponding angles can help you do this by providing a way to measure the angles between two points on a map or between two landmarks in the real world.
2. Construction: Corresponding angles are also used in construction and engineering. When building structures such as bridges and buildings, it is important to ensure that all angles are accurate and consistent. Corresponding angles can be used to check that the angles on each side of a structure are equal, which helps to ensure that the structure is stable and safe.
3. Geometry: Corresponding angles are a fundamental concept in geometry. They are used to prove theorems and solve problems in various branches of mathematics. For example, corresponding angles can be used to prove that two triangles are similar or to calculate the length of sides and angles in a triangle.
4. Art and design: Corresponding angles can also be used in art and design. Many artistic compositions use corresponding angles to create a sense of balance and harmony. By arranging objects or elements in a composition so that they form corresponding angles, artists and designers can create a visually pleasing and aesthetically pleasing composition.
5. Robotics and automation: Corresponding angles are used in robotics and automation to program machines to perform specific tasks. By using corresponding angles, engineers and programmers can ensure that machines move and perform tasks in a consistent and efficient manner.

Conclusion

In conclusion, corresponding angles are pairs of angles that are in matching positions on two intersecting lines, with a third transversal line. They are important in geometry and help us understand more complex concepts. Corresponding angles are congruent, meaning they have the same measurement, and are in the same position on two different lines. They are also formed by alternate interior angles. Understanding corresponding angles is crucial to solving many problems in geometry and can be applied in various mathematical applications.