Cube Definition

A 3-dimensional object with six congruent square-shaped face dimensions of all 6 square faces of the cube is the same. A cube can also be called a regular hexahedron or a square prism. A cube can be anything from an ice cube to a Rubik's cube to a conventional dice. Let's start with a cube and its formulae, followed by a few solved examples and practice questions. Now the question arises what the definition of the cube is? A cube is a three-dimensional permanent structure with six square faces; all sides are the same length. It is one of the five platonic solids and a regular hexahedron. 6 Six square faces, eight vertices, and twelve edges make up the form. Because a cube is a square with all sides the same length, width, and height are all the same measurement. The faces of a cube have a common boundary known as the edge, which is regarded as the edge's bounding line. The shape of the cube is considered cubic, and it is also the fact that the cube is considered a block where all the lengths, breadth and height parameters are the same.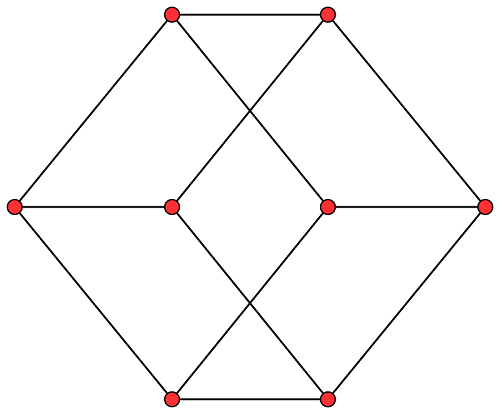

Surface Area and Volume of the Cube

For any shape, the Area of the shape is defined as the region it occupies on the plane. Because a cube is a three-dimensional object, its occupies Area will be on a three-dimensional plane. Because a cube has six faces, we must compute the surface area of the cube covered by each face. The formula is simple and easy to understand

Let A be the edge of the cube

Area of its one surface = a²

And also cube, has 4 lateral surface

Lateral surface area =4 X Area of the one face

LSA=4a²

Now,

The Total Surface Area =LSA + Area of top and bottom faces

TSA=4a²+a²+a²

TSA=6a²

Now we are calculating the volume of the cube as it is well known it is the space contained in it; if a thing is cubical and we need to submerge any substance in it, like water, then the amount of water in gallons to be retained in the object is computed by its volume. The volume formula is as follows:

It is given by the volume of the cube: a³

Properties of the Cube

• The properties of the cube are:
• All the face of the cube is square
• The plane angles of the cubes are the right angle.
• All the faces or sides have almost equal dimensions
• Four faces meet each face
• The edges opposite to each other are parallel

What is the Difference Between a Cube and a Square?

The main distinction between the square and the cube is that the square is a two-dimensional figure with just two dimensions (length and width), whereas the cube is a three3-dimensional shape with three dimensions (length, breadth, and height). The cube is formed from a square.

Some Solved Examples

Example 1

Find a cube's surface area and volume with a side length of 12 cm.

Solution:

Provided, a = 12 cm on either side

As a result, using the cube's surface area and volume equations, we may write;

Surface Area = 6a² = 6(12)² = 6(144) = 864 cm2.

Volume =a³ = 12³ = 1728 cm³

Example 2

Determine the side length of a cube with a volume of 512 cm³.

Solution:

Given: cube volume, v = 512 cm².

We know that the formula for the volume of a cube is a³ cubic units.

As a result, 512 = a³.

The number 512 may be written as 8³.

8³ = a³ Hence, a= 8

Consequently, the side length of the cube, a = 8 cm.

Example 3

Every side of a cuboid is equivalent to 10 cm. What is the cube's volume?

Solution:

Let's use the formula to get the volume of a cube with a side of a. Volume of a cube = a³ = 10 X10 X10 = 1000 cm3.

Geometric Relations

A cube contains eleven nets, There are eleven methods to flattening a hollowed cube by removing seven edges. The cube is the cell of four Euclid spaces' sole regular tiling. It is also the only Plato solid with faces with an even number of sides, making it the only zonohedron among the Basic shapes (every face has point symmetry). A cube's vertices can be divided into two groups of four, each producing a regular triangular prism known as a demi cube. The Stella octangular is a regular compound formed by these two elements. The two intersect to make a regular octahedron. A regular tetrahedron's symmetries correspond to those of a cube, which maps each tetrahedron to itself; the cube's additional symmetry map the two to each other.

Cubic Graph

The cube's skeleton (vertices and edges) produces the cube graph, which has eight vertices and 12 edges. It is a subset of the hypercube graph. It is one of 5 Platonic graphs, each a skeleton of its Platonic solid. The three-dimensional k-ARY Hamming graph, the cube graph for k = 2, is an extension. This type of graph may be found in the theory of parallel processing in computers.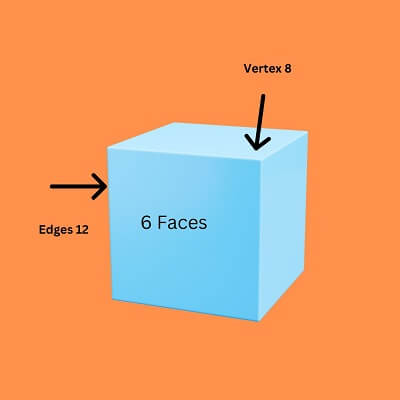

The Diagonal of the Cube

A cube has two kinds of diagonals: facing diagonal lines and major diagonals. The diagonal of a cube is the line that connects the cube's opposite corners. A diagonally facing is a line that connects the opposing vertex of a cube's face and is a square root two times the length of a cube's side. The major diagonal is the straight path that connects the opposing vertices and passes through the center of the cube, and it equals the cube root of 3 times the length of a cube's side. The cubes have a total of Twelve face diagonals due to their six faces.