Define integral Formula

Introduction

Integration is an essential concept in mathematics with a few applications in different fields. In numerical terms, integrals are characterized by limits, a highly perplexing subject we will cover later in the article.

Integrals are defined as the limit of the sum of small parts which are so small that these parts are termed as "Infinitely" small parts which, when added in infinitely many numbers, make up the integral for that interval.

This article will cover the main ideas of integration and its formulae with use cases and applications. The integration utilizes a few techniques, like substitution and integration by parts.

What is Integral?

In mathematics, the integral is the formulae or an equation that relates a function to its integral value. The integral value expresses the area under the curve or the volume of solid occupied in terms of function. It is dependent on how it is defined.

The basic formula of integration is ∫ f(x) dx = F(x) + C

Where the ∫ denotes the integration symbol, f(x) denotes the integrand, and dx is the variable of integration. In contrast, F(x) is the antiderivative of f(x).

The antiderivatives of a function are another function that, on differentiation, gives out the original function. At the same time, the constant of integration is the family of functions that may be constant.

Formulae of integration for different functions

• Power Rule: ∫ x^n dx = (x^(n+1))/(n+1) + C, where n is any real number except for -1
• Exponential Rule: ∫ e^x dx = e^x + C

Trigonometric Rule:

• ∫ sin(x) dx = -cos(x) + C
• ∫ cos(x) dx = sin(x) + C
• ∫ sec^2(x) dx = tan(x) + C
• ∫ csc^2(x) dx = -cot(x) + C
• ∫ tan(x) dx = ln|sec(x)| + C, where ln is natural log or log with base e.
• ∫ cot(x) dx = ln|sin(x)| + C

Inverse Trigonometric Rule:

• ∫ 1/(1+x^2) dx = arctan(x) + C
• ∫ 1/(√(1-x^2)) dx = arcsin(x) + C
• ∫ 1/(x^2+1) dx = arctanh(x) + C

Logarithmic Rule: ∫ 1/x dx = ln|x| + C

• Integration by Parts Rule: ∫u dv = uv - ∫v du, where u and v are functions of x and dv and du are their respective derivatives

Different types of integration techniques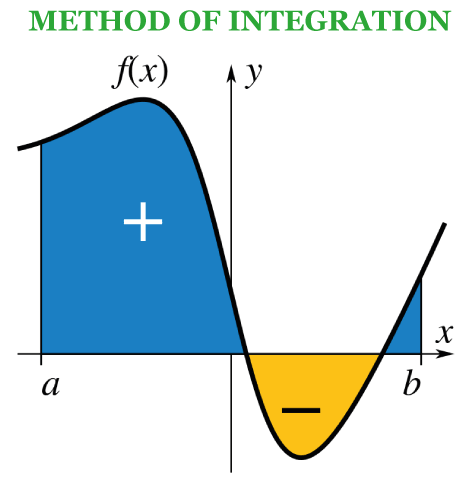

The integration uses direct formulae and different techniques that help solve complex integration problems.

1. Substitution: The most important of all methods is the substitution technique involves substituting a new variable for a complicated expression within the integral. The above technique is explained with the help of solved examples.

Let say we have f(x) = (3x^2 + 2x + 1)√(x^3 + x + 1)

In order to integrate it we have , ∫(3x^2 + 2x + 1)√(x^3 + x + 1) dx

• Let us suppose u = x^3 + x + 1. Then du/dx = 3x^2 + 1, so dx = du/(3x^2 + 1).on substituting value of u, we get:
  ∫(3x^2 + 2x + 1)√(x^3 + x + 1) dx = ∫(3x^2 + 2x + 1)√u du/(3x^2 + 1)
• On further Simplifying, we get the following:
  ∫(2/3)√u du + ∫(1/3)x√u du + ∫(1/3)√u du
• Using the power rule for integration, we get the following:
  (4/5)(x^3 + x + 1)^(5/2) + (1/9)(x^3 + x + 1)^(3/2) + (2/3)(x^3 + x + 1)^(3/2) + C
  Here, C is the constant of integration.

2. Integration by Parts: This technique involves solving integration by breaking up an integral into two parts and applying a formula that involves the product rule for derivatives. An example has been solved to give better clarity:

• Let us assume a function g(x) =x sin(x)
  So, ∫g(x)= dx ∫x sin(x) dx
• Using the integration by parts formula, let u = x and dv/dx = sin(x), so du/dx = 1 and v = -cos(x). Then: ∫x sin(x) dx = -x cos(x) + ∫cos(x) dx
• Using the power rule for integration, we get -x cos(x) + sin(x) + C, where C is the constant of integration.

3. Partial Fraction method: The partial fraction method or technique involves breaking up a complicated rational function into simpler and smaller fractions and then integrating each fraction. Here is an example:

• Let us assume h(x) = (x + 2)/(x^2 + 3x + 2)
  So, ∫h(x)dx = ∫(x + 2)/(x^2 + 3x + 2) dx
• On further factoring the denominator, we will get:
  (x + 2)/(x^2 + 3x + 2) = (x + 2)/[(x + 1)(x + 2)]
• In Simplifying, we get the following:
  (x + 2)/[(x + 1)(x + 2)] = 1/(x + 1) - 1/(x + 2)
• Finally we have, ∫h(x) dx = ∫(x + 2)/(x^2 + 3x + 2) dx = ∫1/(x + 1) dx - ∫1/(x + 2) dx

4. Trigonometric Substitution: The trigonometric substitution method involves substituting trigonometric functions for complicated algebraic expressions in the integral equation. Here is an example to demonstrate the whole process:

B(x) = √(x^2 + 1)

So , ∫B(x) dx = ∫√(x^2 + 1) dx

• Let x = tan(theta). Then: dx/d(theta) = sec^2(theta)
• Substituting, we get: ∫sec^3(theta) dtheta
• Using the power rule for integration, we get the following: (1/2)

Some FAQS related to the integral formulae

1. What do you mean by integral formulae?

Ans: It is a mathematical expression or mathematical equation that provides a way or method to calculate the integral value. Moreover, as we know from the previous discussion, the integral measures area under the curve.

2. What is the difference between the definite and indefinite types of integration?

Ans: When defined in terms of the area under the curve, a definite integration is a method to calculate the area under the curve for a definite interval or between two definite limits, while indefinite integration gives us a general solution for the area under the curve which is applicable for a set of the same type of functions.

3. Write about the most commonly used integral formulae.

Ans: The most commonly used Formula for integration is the definite integral Formula of form ∫f(x)dx. It is used to find the area under a curve between two limits. It is an essential tool in calculus and mathematical analysis. The Formula can be used to calculate integrals of various functions. It can be extended to higher dimensions for use in multivariable calculus.

4. How do I know which integral Formula to use?

Ans: To determine which integral Formula to use, you need to consider the function being integrated, the limits of integration, and any special conditions or properties that may apply. Here are some general guidelines:

• Identify the type of function being integrated (trigonometric, exponential, polynomial, etc.) and use the corresponding Formula.
• Determine whether the integral is definite or indefinite. Definite integrals have specific limits of integration, while indefinite integrals do not.
• For definite integrals, ensure that the limits of integration are consistent with the integrated function.
• If the integrated function is complex, try using advanced techniques such as integration by parts or substitution.
• For indefinite integrals, check for any special conditions or properties, such as symmetry, periodicity, or odd/even functions.

Consult an integral table or use computer software to check your work when in doubt. Remember that practicing solving integrals of different functions with varying degrees of complexity can help you become more comfortable identifying the appropriate integral Formula.