Hooke's Law Definition

According to the physics concept known as Hooke's law, an elastic material will deform or change in length in proportion to the force applied to it. As long as the applied force is within the material's elastic limit, it is stated that a material's degree of deformation is exactly proportional to the force applied to it.

F = -kx, where F is the applied force, x is the resultant deformation or change in length of the material, and k is the spring constant, which is a gauge of the material's stiffness, is how Hooke's law is mathematically stated. A force acting in the opposing direction to that of the deformation is indicated by a negative sign.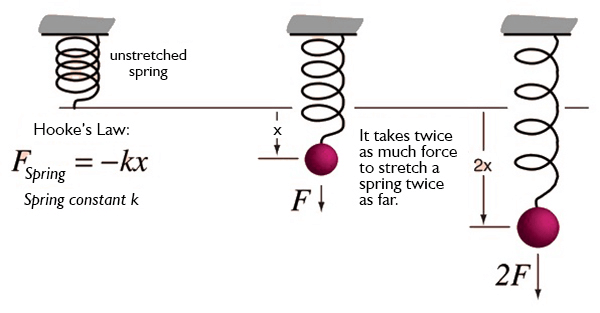

As long as the applied force does not go beyond the material's elastic limit, Hooke's rule is applicable to the majority of elastic materials, including springs and rubber bands. Beyond this point, the substance will experience permanent, irreversible plastic deformation.

Stress and strain are other ways to convey Hooke's law. Stress is the force that develops on individual units of a material as a consequence of an externally applied force. The relative deformation brought on by tension is known as strain. Stress and strain are inversely correlated for comparatively low stresses.

Imagine a spring suspended from a ceiling to get a sense of how Hooke's rule functions in real life. The spring will stretch if you hang a weight from the end of it; the quantity of stretching is proportional to the weight of the object. The spring will expand more as you put on more weight, but only so far. The spring will eventually hit its elastic limit and will become permanently deformed if any additional weight is applied.

Despite being a straightforward and elegant concept, Hooke's law has significant ramifications for numerous fields of science and engineering. For instance, it is widely used to ensure that mechanical systems, such as the suspension systems for cars and trucks, are both secure and effective.

The fact that Hooke's law only pertains to elastic materials is an important aspect of it. Hooke's law will not hold true if a material does not show a linear relationship between force and deformation. A piece of plastic, for instance, will not act in accordance with Hooke's law if you attempt to stretch it because it will deform due to plastic deformation and not revert to its original shape after the force is removed.

The notion of stress and strain is a key one that relates to Hooke's law. Strain is the resultant deformation per unit length, whereas stress is the force imparted to a material per unit area. In terms of stress and strain. Hooke's law can be rewritten in terms of stress and strain as ? = E?, where ? is the stress, ? is the strain, and E is the modulus of elasticity, which is a measure of the stiffness of the material.

In materials science and engineering, where it is used to examine the mechanical properties of materials, Hooke's law also has significant uses. For instance, you can determine the modulus of elasticity of a substance by applying a force to it, measuring the resulting deformation, and then using Hooke's law to determine how stiff or flexible the material is.

Hooke's law is crucial from a theoretical standpoint in addition to its practical uses. Many other physical laws are drawn from similar linear relationships, making it one of the simplest instances of a relationship between two variables. In this respect, Hooke's law is a physics fundamental that forms the basis of much of our knowledge of the natural world.

History of Hooke's Law

Robert Hooke is renowned for his contributions to physics, mathematics, and astronomy, among other scientific disciplines. He was born in Freshwater, England, in 1635, and subsequently attended Oxford University. He was given the job of curator of experiments at the newly established Royal Society in 1660, where he carried out a great deal of research and produced a great deal of discoveries.

Hooke's rule was one of the greatest discoveries he made in the field of physics. He released a book titled "Lectures de Potentia Restitutiva" in 1676 that contained the results of his experiments involving springs and elastic substances. As long as the force is within the material's elastic limit, he claimed in this book, the deformation of an elastic material is immediately proportional to the force given to it. A measure of an elastic material's stiffness, the spring constant was another idea he proposed.

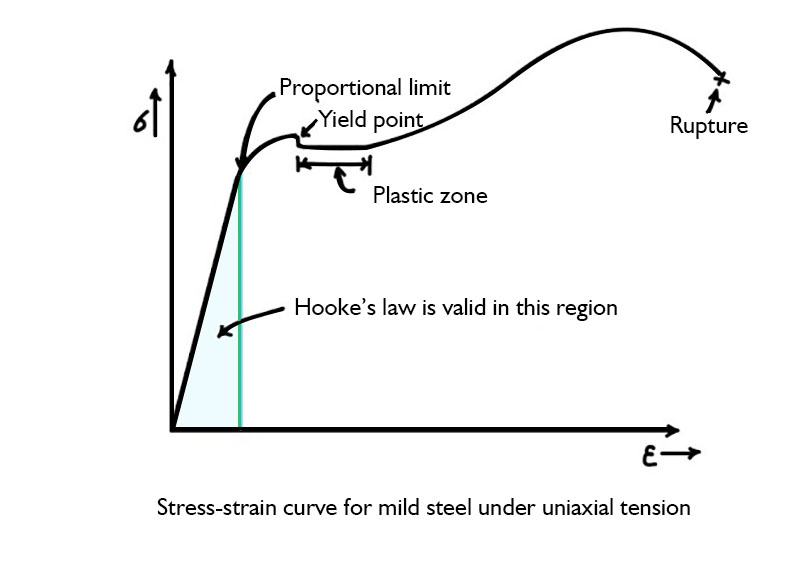
Applications of Hooke's Law

The applications of Hooke's law are many and varied, and they have been used in various fields, including engineering, biology, and medicine.

1. Springs

Spring applications of Hooke's rule are among the most well-known. From toys and jewellery to industrial equipment and transportation, springs have a broad range of uses. Hooke's law states that a spring's deformation is precisely proportional to the force acting on it. As a result, springs can be used to store energy and cushion shock.

2. Elasticity

Hooke's rule is also used to explain how elastic materials behave. Elastic materials are those that can be deformed and then revert to their initial shape. According to Hooke's law, the amount of deformation in an elastic substance is proportional to the force applied to it. As a result, Hooke's law can be used to forecast how elastic materials will behave under stress.

3. Materials Testing

In materials testing, Hooke's law is frequently applied to ascertain a material's mechanical characteristics, such as its flexibility and strength. Engineers can determine a material's Young's modulus, which is a measure of stiffness, by measuring the amount of deformation in the material under a given amount of stress.

4. Biomechanics

The study of biological systems' mechanics, known as biomechanics, makes significant use of Hooke's law. For instance, the tendons and ligaments in the human body are just a couple of the many structures that act like springs. Biomechanics researchers can examine how these structures behave under various loads and movements by using Hooke's rule.

5. Prosthetics

Prosthetic limb design also makes use of Hooke's rule. Engineers can create prosthetics that mimic the behaviour of the body's natural structures by knowing how these structures respond to various loads and motions. This can enhance the comfort and usability of prosthetic arms.

6. Acoustics

Acoustics uses Hooke's rule to explain how sound waves behave. A sound wave causes the elements in a medium to vibrate as it passes through it. According to Hooke's law, the quantity of vibration is proportional to the amplitude of the sound wave.

7. Optics

The behaviour of lenses and mirrors is also described by Hooke's rule in the field of optics. A lens or mirror will subtly deform when light passes through it or reflects off of it. Hooke's law states that the quantity of deformation is proportional to the force applied to the lens or mirror.

8. Seismology

Seismology uses Hooke's law to analyse earthquakes and other seismic occurrences. The earth's crust deforms under tension in a way that is comparable to how elastic materials behave. Seismologists can forecast how the earth's crust will respond to various loads and movements by using Hooke's rule.

9. Geology

In order to understand the behaviour of rocks and other geological materials, geologists also use Hooke's rule. Geologists can ascertain the mechanical characteristics of a rock, such as its elasticity and strength, by measuring the amount of deformation in the rock under a given amount of stress.

Limitations of Hooke's Law

Here are some of the limitations and assumptions of Hooke's Law:

1. Elastic Limit

Only up to a material's elastic limit, past which the material deforms plastically, does Hooke's Law hold true. Since plastic deformation occurs when materials are subjected to large forces or stresses, such as metals, it cannot be used to explain the behaviour of these materials.

2. Linear Elasticity

According to Hooke's Law, a material's deformation is assumed to be linearly proportionate to the applied force. But a lot of materials don't respond linear elastically, especially under high stresses or strains. Therefore, only materials with linear flexibility can be used with Hooke's Law.

3. Homogeneity and Isotropy

According to Hooke's Law, a homogeneous, isotropic material has constant properties in all dimensions. However, many materials, especially composites and layered constructions, are not homogeneous or isotropic. In these circumstances, Hooke's Law might not be relevant, necessitating the use of more intricate models to explain their behaviour.

4. Temperature and Time Effects

According to Hooke's Law, a material's characteristics are presumptively unaffected by temperature or time. However, many substances, especially polymers or viscoelastic substances, show temperature- or time-dependent behaviour. In these circumstances, Hooke's Law might need to be adjusted to account for these impacts.

5. Small Deformations

According to Hooke's Law, a material's deformations should be minimal in comparison to its size. Large deformations, however, may arise in a variety of real-world applications, including aerospace engineering and bridge design. In these circumstances, Hooke's Law might not be relevant, and more intricate models might be needed to explain the behaviour of the substance.

Hooke's Law Experiment

A basic tenet of physics known as Hooke's Law describes the connection between the deformation of an elastic material and the force acting upon it. English physicist Robert Hooke made this rule known in the 17th century. In this experiment, we'll look at how Hooke's Law-predicted deformation of a spring relates to the power applied to the spring.

Materials

• Spring
• Stand or clamp
• Masses (weights)
• Ruler or measuring tape
• Stopwatch or timer

Procedure

1. Place the support or clamp in place, then fasten the spring to it.
2. Measure the original length of the spring using the ruler or measuring tape.
3. Add a small mass (weight) to the spring, and measure the new length of the spring.
4. Record the applied force, which is the weight of the added mass, in Newtons (N).
5. Repeat steps 3 and 4 for different masses, increasing the weight each time.
6. Record the length and the applied force for each mass added.
7. Plot a graph of the applied force versus the extension of the spring (change in length from the original length).
8. Calculate the spring constant (k) from the graph, which is the slope of the line.
9. Verify if the spring obeys Hooke's Law by checking if the graph is a straight line passing through the origin.

Analysis

• The experiment's data can be used to create a graph showing the relationship between applied power and spring extension. A force-extension or stress-strain curve is the name given to this graph.
• The spring constant (k), a gauge of the spring's rigidity, is represented by the slope of the line. The power necessary to extend the spring by one unit of length is what is meant by this term.
• The normal length of the spring when no force is applied is represented by the intercept of the line with the y-axis.
• If the graph is a straight line passing through the origin, it means that the spring obeys Hooke's Law. This means that the deformation of the spring is proportional to the applied force, and that this relationship is linear.
• If the graph is not a straight line passing through the origin, it means that the spring does not obey Hooke's Law. This may be due to several factors, such as plastic deformation, nonlinear elasticity, or the limitations and assumptions of Hooke's Law.

Conclusion

A basic tenet of physics known as Hooke's Law describes how elastic materials behave. According to this law, the linear connection between the deformation of an elastic material and the applied force. By measuring the applied force and the spring's subsequent deformation, the experiment described above offers a straightforward and useful method to determine whether a spring complies with Hooke's Law. We can figure out the spring constant and check to see if the spring complies with Hooke's Law by graphing the applied force versus the spring's extension.