Trigonometry Definition

We all must have heard the word 'Geometry,' which is a branch of Mathematics that deals with the study of shapes, angles, structures, and methods of their measurements. Apart from these, this branch of mathematics also focuses on the spatial properties of the shapes and structures and their relative configuration in a plane. Geometry is made up of two Greek words, 'Geo' and 'Metron.' The meaning of 'Geo' is 'Earth,' and the meaning of 'Metron' is 'Measurement.' By this, we can say that Geometry is the stream of mathematics that describes to us the measurement of shapes, objects, planets, angles, and more.

Geometry is mainly classified into the following two types according to the dimensions of the shapes:

1. Two-dimensional (2-D) Geometry
2. Three-dimensional (3-D) Geometry

One basic and most important point, which is followed in both 2-D geometry as well as in 3-D geometry, is that all the shapes and structures which are studied in Geometry are formed from the points, rays, lines, and plane surfaces. All the shapes we study in geometry are formed using lines which are intersecting at some common points and form a close structure on a plane surface.

In this vast topic of geometry today, we have a special topic, "Trigonometry," as our discussion topic.

Introduction:

The word "Trigonometry" is made up of two words, first is "Tri-gon," and the other is "Metron," as we have read in the upper paragraph, the word "Metron" means "measure," and the meaning "Tri-gon" is "Three-angled," i.e., a shape or an object that has three angles and sides. This implies that trigonometry is part of geometry, which is a part of mathematics and deals with the study of triangles. This subject has vast applications in different fields, such as engineering, astronomy, physics, and many more. Trigonometry is a very basic part of modern mathematics and is used intensively in our daily lives. In this article, we will explore all the possible parts of trigonometry, such as history, definition, trigonometric functions, inverse trigonometric functions, their applications, and much more.

Definition

Trigonometry is a topic of mathematics, which deals with the study of triangles, and a triangle is a shape or object which has three angles. This implies Trigonometry can be defined as the topic in which we study the relation between the sides and angles of a triangle or a triangular-shaped object.

The three basic trigonometric functions are sine, cosine, and tangent; these functions relate the angle of a right triangle to the ratio of the lengths of its sides.

Overall, trigonometry is a fundamental branch of mathematics that provides a powerful toolkit for solving problems related to triangles, angles, and ratios. It is an indispensable tool for anyone studying science, technology, engineering, or mathematics.

History

In ancient times these trigonometric functions were used by sailors and astronomers as navigating methods to sail in the sea. The discovery of trigonometry can be entitled to ancient Indians, Mesopotamians, and Egyptians around four thousand years ago.

The first evidence of trigonometry was found around 150 BCE by a Hellenistic mathematician, "Hipparchus," it was found that he made a trigonometric functions table with the value at a particular angle. "Ptolemy" further adds a description to the calculations in around 100 BCE. Hipparchus is also known as the father of modern trigonometry.

The famous Indian mathematician and astronomer "Aryabhatta" developed the table for half chords, which is also called the sine table with a cosine table, around 4 AD. He used "zya" as the representation of the sine function and "kotizya" as the representation of cosine, and "Vikram zya" as the representation of the inverse sine function. A famous Indian mathematician, "Brahmagupta," around 6 AD used the interpolation formulas to calculate the value of the sine function up to the second order of Newton's Stirling interpolation formula.

In ancient Shri Lanka, in the Anuradhapura kingdom at that time, a very old reservoir is present. It is proved by Archeological research that to make this reservoir, ancient people used trigonometry to calculate the gradient of water flow around 4 BCE.

In the 10th century, a Persian mathematician and astronomer, Abul Wafa, discovered the tangent function; he also improved the calculating methods of trigonometry to calculate the trigonometry table. He found a way to calculate angle addition, i.e., sin (a + b), and build the formula of spherical geometry.

Sin (A) / Sin (a) = Sin (B) / Sin (b) = Sin (C) / Sin (c).

Where A, B, and C are angles of a triangle and a, b, and c are lengths of sides of that triangle (ABC).

An Indian mathematician, "Bhaskara," in 1150, gave detailed methods to construct trigonometric values; he also developed formulas for spherical trigonometry, in the 13th century, Bhaskara, along with Persian mathematician Nasir al-Din Tusi was the first to treat trigonometry as a distinct mathematical discipline.

The word "Trigonometry" was coined in 1595 by a mathematician Bartholemaeus Pitiscis, mentioned in his work (thesis) on trigonometry.

Trigonometric Functions

There are mainly three trigonometric functions that are Sine, Cosine, and Tangential. But there are other three functions also that are related to the above three (we will discuss the relation in upcoming paragraphs), these functions are Cosecant, Secant, and Cotangential.

To understand these functions we will draw a right-angled triangle (XYZ), which has a 90 degrees angle on the Y vertex, such that XY is the perpendicular of the triangle, YZ is the base of the triangle, and XZ is the hypotenuse of the triangle XYZ. The angle between the perpendicular and the hypotenuse is X, the angle between the base and the hypotenuse is Z, and the angle between the perpendicular and the base is Y which is 90 degrees. Let the length of the perpendicular is z, the length of the hypotenuse is y, and the length of the base is x.

As shown in the picture below.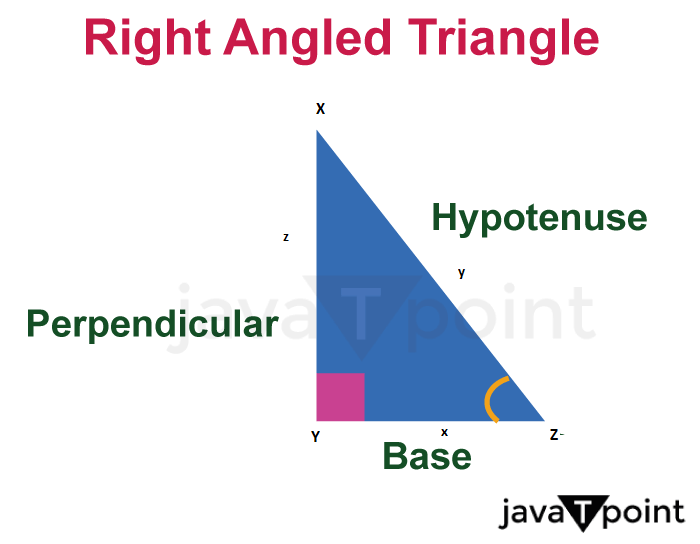

1. Sine Function: A sine function can be defined as the ratio of the perpendicular and the hypotenuse of triangle XYZ. It is denoted by Sin.
   This implies Sin (Z) = perpendicular / hypotenuse = z / y
   When the angle is changed in the sine function the perpendicular and base also change with respect to the angle.
   Sin (X) = perpendicular / hypotenuse = x / y
2. Cosine Function: A cosine function can be defined as the ratio of the base and the hypotenuse of triangle XYZ. It is denoted by Cos.
   This implies Cos (Z) = base / hypotenuse = x / y
   When the angle is changed in the cosine function the perpendicular and base also change with respect to the angle.
   Cos (X) = base / hypotenuse = z / y
3. Tangent Function: A tangent function can be defined as the ratio of the perpendicular and the base of triangle XYZ. It is denoted by Tan.
   This implies Tan (Z) = perpendicular / base = z / x
   When the angle is changed in the tangent function the perpendicular and base also change with respect to the angle.
   Tan (X) = perpendicular / base = x / z
4. Cosecant Function: A cosecant function can be defined as the ratio of the hypotenuse and the perpendicular of triangle XYZ. It is denoted by Cosec or Csc.
   This implies Cosec (Z) = hypotenuse / perpendicular = y / z
   When an angle is changed in the cosecant function the perpendicular and base also change with respect to the angle.
   Cosec (X) = hypotenuse / perpendicular = y / x
5. Secant Function: A secant function can be defined as the ratio of the hypotenuse and the base of triangle XYZ. It is denoted by Sec.
   This implies Sec (Z) = hypotenuse / base = y / x
   When an angle is changed in the secant function the perpendicular and base also change with respect to the angle.
   Sec (X) = hypotenuse / base = y / z
6. Cotangent Function: A cotangent function can be defined as the ratio of the base and the perpendicular of triangle XYZ. It is denoted by Cot.
   This implies Cot (Z) = base / perpendicular = x / z
   When the angle is changed in the cotangent function the perpendicular and base also change with respect to the angle.
   Cot (X) = base / perpendicular = z / x

Important Formulas

1. [Sin (Θ)]² + [Cos (Θ)]² = 1
2. 1 + [Tan (Θ)]² = [Sec (Θ)]²
3. 1 + [Cot (Θ)]² = [Cosec (Θ)]²
4. Sin (Θ) = 1 / Cosec (Θ)
5. Cos (Θ) = 1 / Sec (Θ)
6. Tan (Θ) = 1 / Cot (Θ)
7. Sin (-Θ) = -Sin (Θ)
8. Cos (-Θ) = Cos (Θ)
9. Tan (-Θ) = -Tan (Θ)

Sum and Product Formulas: Where α is greater than β, α ≥ β.

1. Sin (α) + Sin (β) = 2 * Sin [(α + β)/2] * Cos [(α - β)/2]
2. Sin (α) - Sin (β) = 2 * Sin [(α - β)/2] * Cos [(α + β)/2]
3. Cos (α) + Cos (β) = 2 * Cos [(α + β)/2] * Cos [(α - β)/2]
4. Cos (α) - Cos (β) = - 2 * Sin [(α + β)/2] * Sin [(α - β)/2]

Formulas for product to sum: Where α is greater than β, α ≥ β.

1. Sin (α) * Sin (β) = (1/2) * [Cos (α - β) - Cos (α + β)]
2. Cos (α) * Cos (β) = (1/2) * [Cos (α + β) + Cos (α - β)]
3. Sin (α) * Cos (β) = (1/2) * [Sin (α + β) + Sin (α - β)]
4. Cos (α) * Sin (β) = (1/2) * [Sin (α + β) - Sin (α - β)]

Formulas for Sum of Angles: Where α is greater than β, α ≥ β.

1. Sin (α + β) = Sin (α) * Cos (β) + Cos (α) * Sin (β)
2. Sin (α - β) = Sin (α) * Cos (β) - Cos (α) * Sin (β)
3. Cos (α + β) = Cos (α) * Cos (β) - Sin (α) * Sin (β)
4. Cos (α - β) = Cos (α) * Cos (β) + Sin (α) * Sin (β)
5. Tan (α + β) = [Tan (α) + Tan (β)] / [1 - Tan (α) * Tan (β)]
6. Tan (α - β) = [Tan (α) - Tan (β)] / [1 + Tan (α) * Tan (β)]

Half Angle Formulas:

1. Sin (A/2) = ± √{(1 - Cos (A))/2}
2. Cos (A/2) = ± √{(1 + Cos (A))/2}
3. Tan (A/2) = ± √{(1 - Cos (A))/ (1 + Cos (A))} = sin (A) / [1 - Cos (A)]

Relation between Sides and Angles of a Triangle

Let us draw a regular triangle (XYZ), X, Y, and Z are angles of the triangle.

Such that the length of XY = z, YZ = x, and XZ = y. As shown in the figure.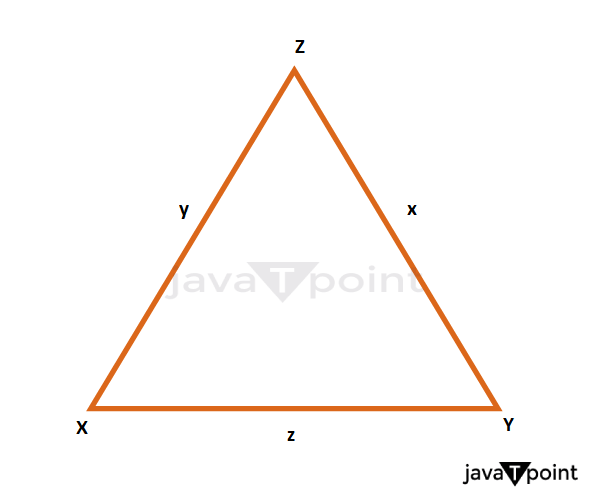

Then the relation between the sides and angles of the triangle is given by:

1. [Cos (X)] * [2*y*z] = z² + y² - x²
2. [Cos (Y)] * [2*x*z] = x² + z² - y²
3. [Cos (Z)] * [2*x*y] = x² + y² - z²
4. [x / Sin (X)] = [y / Sin (Y)] = [z / Sin (Z)] = 2*R, where R is the circiumcircle of the triangle.

Trigonometry Value Table

In this table, we get to know about some values of trigonometric functions at 0, 30, 45, 60, and 90 degrees.

Degrees

Inverse Trigonometric Functions

Inverse trigonometric functions are functions that are the inverse of the six trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. These functions are used to find the angle measures that correspond to the given values of the trigonometric functions.

Sin (Θ) = x

Θ = Sin^-1 (x)

The six inverse trigonometric functions are

1. Arcsine (x): The inverse sine function, it gives the angle whose sine is x. Its domain is [-1, 1], and its range is [-?/2, ?/2].
2. Arccosine (x): The inverse cosine function, it gives the angle whose cosine is x. Its domain is [-1, 1], and its range is [0, ?].
3. Arctangent (x): The inverse tangent function, it gives the angle whose tangent is x. Its domain is (-∞, ∞), and its range is (-?/2, ?/2).
4. Arcscent (x): The inverse secant function, it gives the angle whose secant is x. Its domain is (-∞, -1] ? [1, ∞), and its range is [0, ?/2) ? (?/2, ?].
5. Arccosecent (x): The inverse cosecant function, it gives the angle whose cosecant is x. Its domain is (-∞, -1] ? [1, ∞), and its range is (-?/2, 0] ? [0, ?/2).
6. Arccotangent (x): The inverse cotangent function, it gives the angle whose cotangent is x. Its domain is (-∞, ∞), and its range is (0, ?).

It is important to note that the inverse trigonometric functions have restrictions on their domains and ranges, and they are not always single-valued. In order to obtain a unique value, a principal value is usually defined.

Applications of Trigonometry

Trigonometry has a vast range of applications in different fields such as:

1. Physics: Trigonometry is used to calculate the trajectories of moving objects and the angles of incidence and reflection of light.
2. Engineering: Trigonometry is used to design and build structures such as buildings, bridges, and dams.
3. Astronomy: Trigonometry is used in astronomy to calculate the positions and movements of celestial objects such as stars and planets and their distances from Earth.
4. Music: Trigonometry is used in music to calculate the frequencies and wavelengths of sound waves.
5. Surveying: Trigonometry is used in surveying to measure the distances and angles between points on the Earth's surface.
6. Weather Forecasting: Trigonometry is used in weather forecasting to calculate the trajectories and speeds of atmospheric systems.
7. Sports: Trigonometry is used in sports such as baseball, football, and golf to calculate the angles and distances needed for accurate performance.
8. Art: Trigonometry is used in art to create perspective and proportion in drawings and paintings.
9. Cryptography: Trigonometry is used in cryptography to create and decode secret messages.
10. Navigation: Trigonometry is used in navigation to determine the position of a ship or aircraft. By using trigonometry, navigators can calculate the distance between two points, the direction, and the speed of a vessel.