Factor Definition Math
Mathematics is everywhere, from counting our change to calculating the trajectory of a rocket. Mathematics is an important aspect of our daily lives. One of the fundamental concepts in mathematics is the study of factors. In short, when we multiply two numbers to generate another number, these two numbers are called factors of the generated number. Factors are used in many mathematical applications, such as finding the highest common factor (HCF) and the least common multiple (LCM) of two or more numbers, simplifying fractions, and solving equations. In this article, we will delve deeper into the concept of factors and discuss their definition, types, properties, various methods for finding them, their applications, and some examples. Whether you are a student of mathematics or simply someone who wants to understand the basics of factors, here is a detailed overview of this important mathematical concept.
Definition of Factors
Factors can be simply defined as numbers that we can multiply together to get a different number. For example, the factors of 18 are 1, 2, 3, 6, 9 and 18 because you can multiply some combination of these numbers (like 2 and 9 or 3 and 6) to get 18.
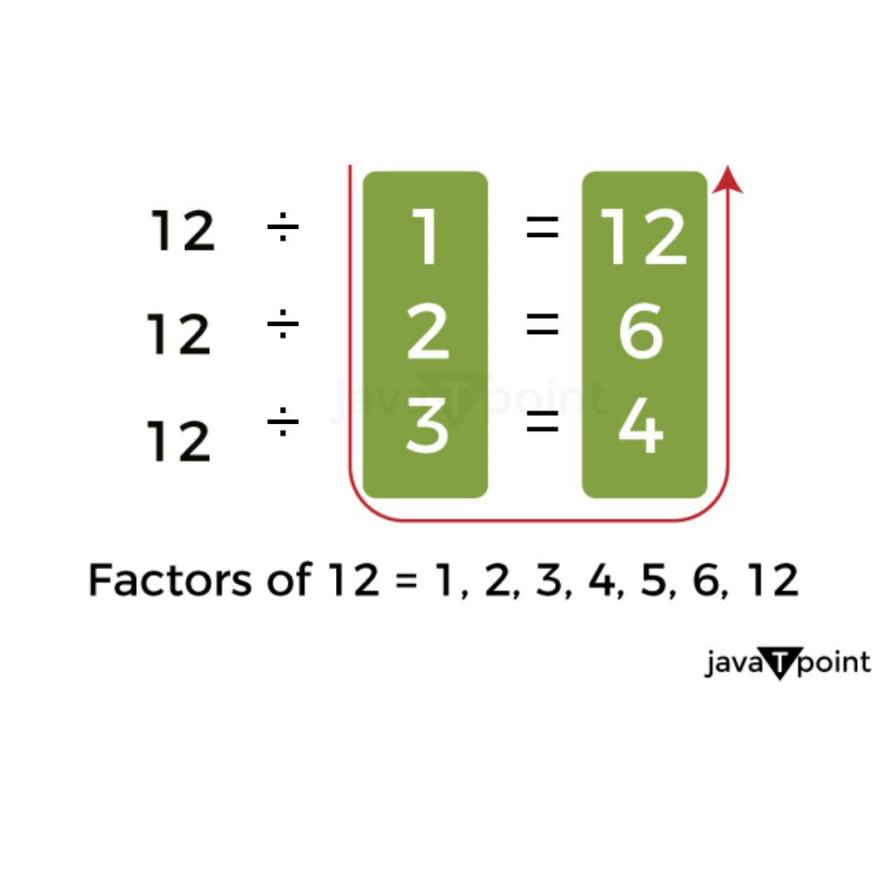
Factors are important concepts in mathematics because they help us understand the relationships between numbers and they are used in various calculations and as well as solving real-life problems.
Types of Factors
Factors are mainly of the following three types: Prime factors, Composite factors, and Relative prime factors.
- Prime factors: As their name suggests, these are the factors that are prime numbers. The numbers that are only divisible by 1 and themselves are known as prime numbers. For example, the prime factors of 12 are 2, 2 and 3 because 2 and 3 are both prime numbers and when you multiply 2 � 2 � 3, you get 12.
- Composite factors: Composite factors, on the other hand, are the factors that are not prime numbers. In other words, we can break down the composite factors into smaller factors other than 1 or themselves. For example, the composite factors of 12 are 4 and 6 because 4 can be broken down into 2 � 2, and 6 can be broken down into 2 � 3
- Relative prime factors: Relativeprime numbers are the numbers that have no common factors other than 1. Relatively prime factors are factors of two integers that are relatively prime to each other. For example, the factors of 15 are 1, 3, 5, and 15. The factors of 28 are 1, 2, 4, 7, 14, and 28. The factors of 15 and 28 that are relatively prime to each other are 1 and 7. Therefore, 1 and 7 are the relatively prime factors of 15 and 28.
How to Find Factors
- Listing Factors Method: This is the simplest way to discover the factors of a number. Simply write down every number that divides the provided number without leaving a residual. For instance, we can begin by making a list of all the numbers that divide 12 evenly without leaving a remainder in order to determine its components. 1, 2, 3, 4, 6, and 12 are the numbers. Therefore, 1, 2, 3, 4, 6, and 12 are the factors of 12.
- Prime Factorization Method: A number can be expressed as the product of its prime factors using the prime factorization method. By continually dividing a number by its smallest prime factor up until the quotient is no longer divisible by the lowest prime factor, we can determine the prime factorization of that number. Once we have a product with just prime elements, we must next repeat this method with the quotient. For example, the prime factorization of 24 is 2 x 2 x 2 x 3, because 24 divided by 2 gives 12, 12 divided by 2 gives 6, 6 divided by 2 gives 3, and 3 is a prime number.

- Using a Factor Tree: We call a diagram that shows the factorization of a number into its prime factors, a factor tree. To use a factor tree, we start by dividing the given number into any two factors. We then continue dividing the factors until we reach the prime factors. For example, to find the factors of 36 using a factor tree, we can start by dividing it by 2, giving us 2 and 18. We can then divide 18 by 2, giving us 2 and 9. We can further divide 9 by 3, giving us 3 and 3. Therefore, the prime factorization of 36 is 2 x 2 x 3 x 3.
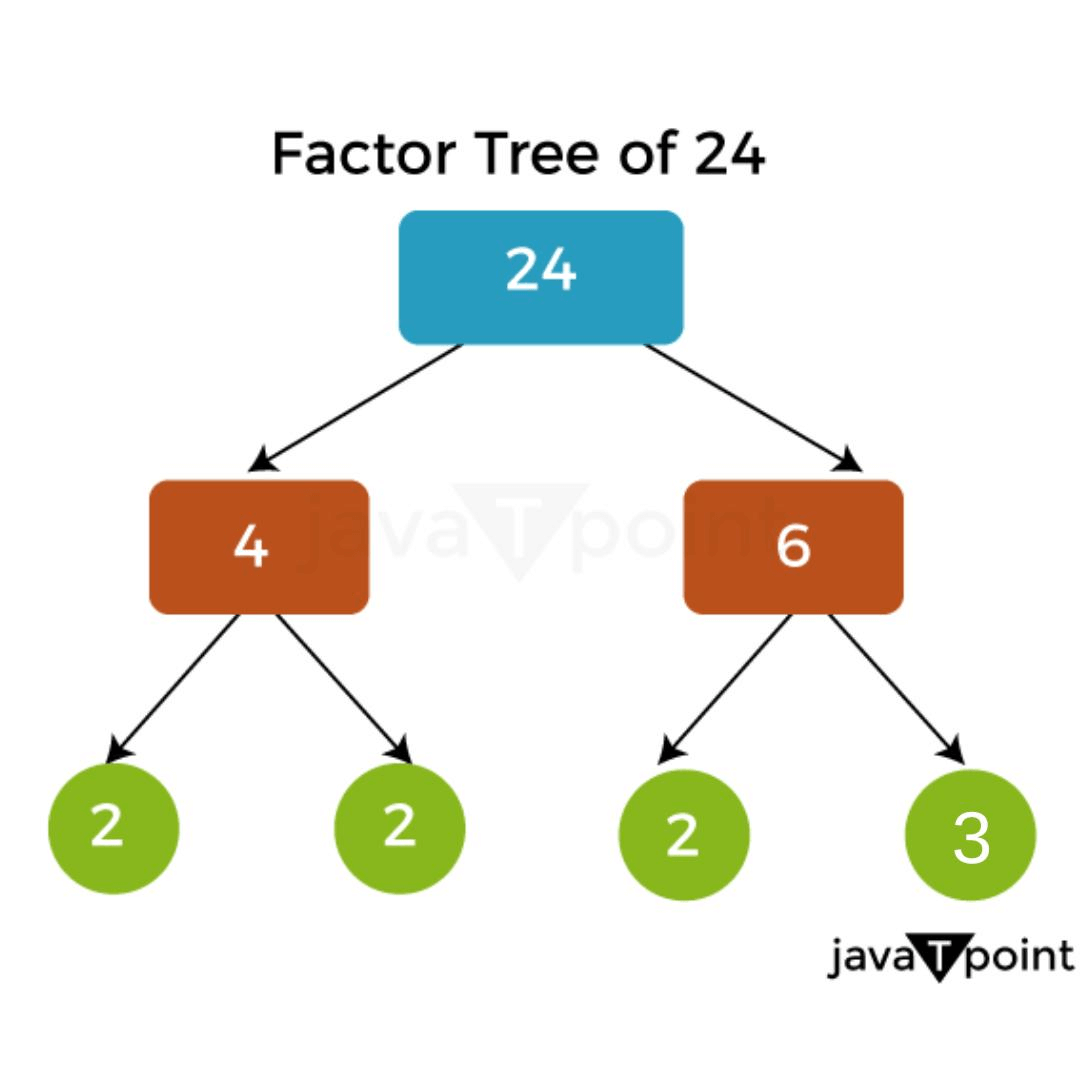
These are the three most commonly used methods to find factors, and each of these has its advantages and disadvantages depending on the number being factored in and the purpose of finding the factors.
Applications of Factors
Factors are used to find the greatest common factor and least common multiple of two or more numbers as well as to identify features of numbers such as primality. They can also be used to simplify equations by rewriting them in more understandable terms. These are only a few examples of the various applications of factors in mathematics.
- Study of Prime Numbers: Prime numbers are those numbers that are only divisible by 1 and themselves. Factors are used in the study of prime numbers to identify which numbers are prime and which are not. For example, if a number has only two factors (1 and the number itself), then it is a prime number.
- Solution of Equations: In algebra, factors are used to solve equations by factoring. Factoring involves finding the factors of a polynomial expression and using them to break it down into simpler terms. This allows us to solve equations that might otherwise be difficult or impossible to solve.
- Computation of Greatest Common Factors (GCF) and Least Common Multiples (LCM): Factors are also used to compute the greatest common factor (GCF) and least common multiple (LCM) of two or more numbers. GCF is the largest factor that two or more numbers have in common, while LCM is the smallest multiple that two or more numbers share. These calculations are often used in fractions, simplifying expressions, and solving word problems.
Some Exercises
Below are some exercises and examples that will help you in gaining a deeper understanding of factors and their practical applications.
Question 1: Identify the factors of the following numbers:
14, 24, 45, 60
Solution:
- Factors of 14: 1, 2, 3, 7, 14
- Factors of 34: 1, 2, 17, 34
- Factors of 45: 1, 3, 5, 9, 45
- Factors of 60: 1, 2, 3, 5, 10, 30, 60
Question 2: Find the prime factors of the given numbers:
36, 58, 70, 90
Solution:
- Prime factors of 36: 2, 2, 3, 3
- Prime factors of 58: 2, 29
- Prime factors of 70: 2, 5, 7
- Prime factors of 90: 2, 3, 3, 5
Question 3: Find the greatest common factor (GCF) and least common multiple (LCM) of the following numbers:
- 14 and 34
- 20 and 30
- 24 and 36
- 24 and 36
Solution:
- Factors of 14: 1, 2, 3, 7, 14
Factors of 34: 1, 2, 17, 34
GCF of 14 and 38 is 2
LCM of 14 and 34 is 238
- Factors of 20: 1, 2, 4, 5, 10, 20
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
GCF of 20 and 30 is 10
LCM of 20 and 30 is 60
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
GCF of 24 and 36 is 12
LCM of 24 and 36 is 72
- Factors of 45: 1, 3, 5, 9, 45
Factors of 25: 1, 5, 25
GCF of 45 and 25 is 5
LCM of 45 and 25 is 225
Question 4: Simplify the following fractions into the lowest terms:
- 12/16
- 30/45
- 24/36
- 15/25
Solution:
- 12/16 = (3 x 4)/ (4 x 4) = 3/4
- 30/45 = (2 x 3 x 5)/ (3 x 3 x 5) = 2/3
- 24/36 = (2 x 2 x 2 x 3)/ (2 x 2 x 3 x 3) = 2/3
- 15/25 = (3 x 5)/ (5 x 5) = 3/5
Conclusion
In mathematics, factors are crucial because they aid in our understanding of how numbers relate to one another and are utilised in a variety of calculations and problem-solving techniques. Prime, composite, and relative prime factors are three different categories of factors. Listing factors, prime factorization, and factor trees are a few techniques for determining a number's factors. Mathematicians use factors for a variety of purposes, such as determining prime numbers, the greatest common factor, and the least common multiple. We can better understand the features of numbers and use them in practical contexts if we have a solid understanding of factors.
|
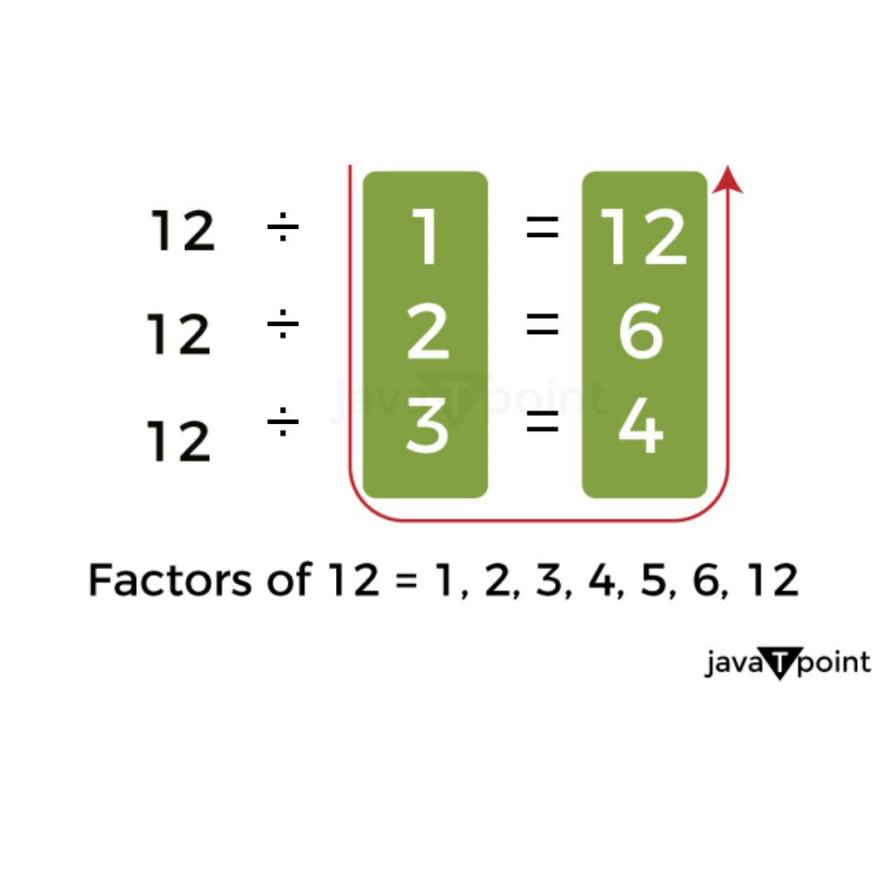
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now












