Vertically Opposite Angles Definition

In geometry when two lines intersect each other, angles are created. Four angles are formed at the intersection point of two lines. Vertical angles are those created at the intersection of two lines that are directly opposite one another. Because they have an identical vertex but are located on different sides of intersecting lines, vertical angles are so named.

Some significant characteristics distinguish vertical angles from other angles. The fact that vertical angles are congruent is one of their most significant characteristics. Congruent describes angles that are the same in size or measure. As a result, once you are aware of one vertical angle's measurement, you are also aware of the other vertical angle's measurement. Vertical angle difficulties can be resolved with this attribute.

The fact that vertical angles are always equal is another characteristic of them. This indicates that the vertical angles will always be equal, regardless of where the crossing lines are placed.Any vertical angle, whether acute (less than 90 degrees), right (exactly 90 degrees), or obtuse (more than 90 degrees), has this property. This characteristic aids in the proof of geometric theorems and the resolution of angle-related issues.

In many branches of mathematics and science, vertical angles are significant. They are employed in geometry to resolve issues requiring angles and to prove theorems. They are also utilised in trigonometry, which is the study of how triangles' angles and sides relate to one another. Vertical angles are utilised in engineering to create structures and buildings as well as in physics to research optics and light.

In conclusion, vertical angles are a crucial geometry topic. They are opposed to one another and are created when two lines intersect. Congruence and equality are two crucial characteristics of vertical angles that make them helpful in resolving angle-related issues. Students who want to thrive in geometry and related areas must understand vertical angles.

Properties of Vertical Angles

When two lines intersect, a kind of angle called a vertical angle is created. These angles stand out from other angles due to a number of characteristics. The congruence of vertical angles is among their most significant characteristics.

Vertical angles are always congruent since they have the same measure as other one. As a result, if angles A and B are vertical angles, their measures will be equal. This characteristic can be helpful in demonstrating geometric theorems and resolving angle-related issues.

The equality of vertical angles is another significant characteristic. In this case, the word "equality" refers to the magnitude of the angles. Vertical angles are always equal, as opposed to some other angles, including supplementary or complimentary angles. This implies that if you are aware of the size of one angle, you are also aware of the size of the other angle. The construction of structures and buildings is just one of the many uses for the equality attribute.

The linear link of vertical angles to other sorts of angles is another characteristic of them. Adjacent angles, for instance, are the other pair of angles that are formed when two lines overlap and create a pair of vertical angles. These adjacent angles combine to form a straight angle of 180 degrees. The linear pair theorem, which is the result of this relationship, can be applied to problems involving angles.

The symmetry of vertical angles is a crucial characteristic. Two pairs of congruent angles can be made by drawing a line through the vertex of two vertical angles. This is due to the symmetrical placement of the vertical angles on either side of the intersecting lines. Applications for this symmetrical trait include the study of optics and light, among others.

Vertical angles are distinctive and helpful in solving difficulties involving angles because of a number of significant characteristics. While their linear relationship and symmetry properties have numerous applications in disciplines like engineering, physics, and optics, their congruence and equality properties are particularly helpful in proving geometric theorems and solving problems. Anyone studying geometry or a related subject must comprehend the characteristics of vertical angles.

Examples of Vertical Angles

Vertical angles are a common geometric concept that can be found in many real-world situations. These angles are formed when two lines intersect, and they are opposite to each other. Here are a few examples of where vertical angles can be found in everyday life:

The creation and construction of structures in architecture often use vertical angles. A roof, for instance, forms two pairs of vertical angles when it is built at an angle to the ground. It's crucial for building design and construction to comprehend the characteristics of vertical angles.

The height of objects is calculated in navigation using vertical angles. As an illustration, you can use vertical angles to calculate the lighthouse's height if you are sailing a ship and spot one. By using this knowledge, the ship can be securely navigated.

The height of things is measured in surveying by using vertical angles, which also helps to produce precise maps. To calculate vertical angles, surveyors utilise specialised equipment, which aids in the production of precise maps and drawings.

For the study of optics and light in physics, vertical angles are crucial. A prism distorts and separates light into its many colours as it flows through it. Due to the different incidence and refraction angles that result in two vertical angles, there is a dispersion that happens.

For the design of bridges and other structures, vertical angles are employed in engineering. When building a bridge over a river, for instance, the height above the water can be calculated using the vertical angles at the top of the bridge. To make sure the bridge is secure and safe, this information is crucial.

To sum up, vertical angles can be seen in a variety of real-world applications, including surveying, navigation, and architectural design. Many disciplines, including physics and engineering, require an understanding of the characteristics of vertical angles. Vertical angles have many uses, and by comprehending these uses, we can better grasp how important vertical angles are to both our everyday lives and the environment we live in.

Vertical Angles Theorem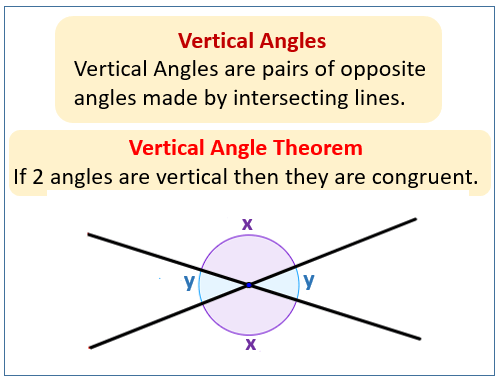

According to this theorem, the vertical angles that are created when two lines cross each other are always congruent. To put it another way, the size of one vertical angle is the same as the size of the other.

Basic geometrical concepts can be used to demonstrate the Vertical Angles Theorem. You can draw two intersecting lines and identify the resulting angles to demonstrate the theorem. The angle addition postulate can therefore be used to demonstrate that the two pairs of vertical angles are congruent.

For example, let's say that we have two intersecting lines AB and CD, and that angles ACD and BDC are vertical angles. We can prove that these angles are congruent by using the following steps:

• Draw a straight line that passes through points A and C.
• Label the angles that are formed by the intersection of the lines AB, CD, and AC.
• Use the angle addition postulate to write an equation for the measure of angle ACD. For example, we can write: m?ACD = m?ACB + m?BCD.
• Repeat step 3 for angle BDC. We can write: m?BDC = m?BDA + m?ADC.

Notice that angles ACB and BDA are alternate interior angles and that angles ADC and BCD are alternate interior angles. By the alternate interior angles theorem, these angles are congruent. Therefore, we can substitute their measures into the equations we wrote in steps 3 and 4.

• Simplify the equations to show that m?ACD = m?BDC. This proves that the two vertical angles are congruent.

Numerous crucial applications of the Vertical Angles Theorem can be found in geometry and related disciplines. It is used, for instance, to demonstrate the corresponding angles theorem and the alternate internal angles theorem, two geometric properties. Additionally, it is employed in the creation of geometric models and in algebraic proofs.

The Vertical Angles Theorem is a crucial characteristic of vertical angles, to sum up. It asserts that the vertical angles created by the intersection of two lines are always congruent. This theorem has a number of significant applications in geometry and related domains and can be proven using fundamental geometry concepts.

Application of Vertical Angles

A wide range of mathematical and scientific domains use vertical angles extensively. The following are some of the main uses for vertical angles:

• Geometry is one area where vertical angles have significant applications. Numerous geometric theorems can be proven using them. The Vertical Angles Theorem, for example, can be used to illustrate the Corresponding Angles Theorem, which states that if two parallel lines are intersected by a transversal, then the pairs of corresponding angles are congruent. This theorem serves as a fundamental building block for many other ideas and is important in many different areas of geometry.
• The building of geometric models, particularly three-dimensional structures like polyhedra, is another significant application of vertical angles. Mathematicians can design exact and aesthetically pleasing geometric models by utilising the characteristics of vertical angles. This has significant ramifications for a variety of industries, including design, engineering, and architecture.
• In order to solve algebraic equations involving angles, vertical angles are also crucial. For instance, we may use the Vertical Angles Theorem to determine the measure of the other angle if we know that two angles are vertical angles and we know the measure of one of the angles. This is helpful for resolving algebraic equations involving angles that appear in disciplines like physics and engineering.
• Angles and their connections to other triangle sides and angles are also a part of trigonometric identities. Trigonometric identities can be proven and new identities can be derived using the characteristics of vertical angles. This has significant uses in the astronomical, surveying, and navigational professions.
• In addition, measuring angles for real-world applications require the use of vertical angles. Vertical angles are used by engineers and architects to create buildings and other structures.

Astronomers use vertical angles to investigate the positions and motions of celestial objects, while surveyors use them to calculate distances and heights. These uses highlight the critical part that vertical angles play in a variety of areas that have a direct bearing on our day-to-day activities.

In conclusion, there are many significant uses for vertical angles across a range of mathematical and scientific disciplines. In practical settings, they are employed to demonstrate geometric theorems, build geometric models, resolve algebraic problems, demonstrate trigonometric identities, and measure angles. Gaining an understanding of many fundamental mathematical and scientific topics requires an understanding of the characteristics and uses of vertical angles.

Conclusion

In conclusion, grasping the concept of vertical angles is crucial to grasp various key mathematical and scientific topics. Vertical angles are generated when two lines connect and are always congruent, opposite to one other, and share a single vertex. They also have other essential qualities, such as being supplementary and creating a type of linear pair with adjacent angles.

One significant property of vertical angles is the Vertical Angles Theorem, which states that the vertical angles that are created when two lines intersect are always congruent. This theorem has several important applications in geometry, algebra, trigonometry, and related subjects. It can be used to establish other theorems, solve algebraic problems, and design geometric models.

Another major application of vertical angles is in the design and construction of buildings and structures. Architects and engineers employ vertical angles to produce exact designs and assure the structural integrity of their projects. Surveyors employ vertical angles to measure distances and heights, while astronomers use them to investigate the positions and movements of celestial objects.

Vertical angles also play a key part in the construction of mathematical and scientific models. They help us comprehend and characterise the behavior of natural phenomena and the physical universe. Without an understanding of vertical angles, it would be impossible to create models that effectively reflect the intricate interactions between diverse variables.

Furthermore, the study of vertical angles helps us to understand the properties of shapes and angles in two and three dimensions. This understanding is vital in subjects like as engineering, architecture, physics, and geometry. It also allows us to address practical challenges in the actual world, such as creating structures and measuring distances.

Overall, vertical angles have numerous vital applications in various mathematical and scientific domains. They play a key role in the development of models that describe natural events, and they are fundamental in the design and construction of buildings and structures. An understanding of vertical angles is also crucial in solving difficulties in domains such as engineering, physics, and geometry. In conclusion, vertical angles are a fundamental idea in mathematics and science, and their study is necessary to comprehending many essential concepts and applications.